算法小抄11-二叉树进阶

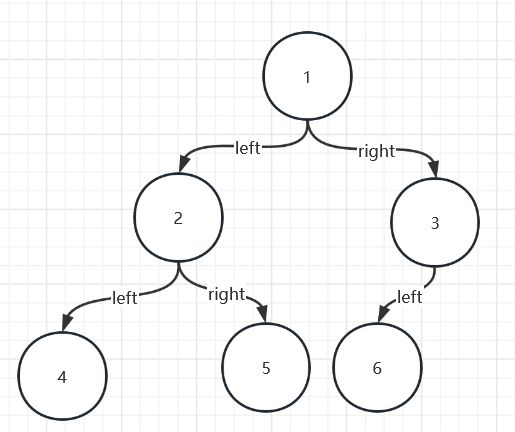
很多二叉树的题目都需要用递归的方式去解决，如果还没有理解递归的话先不要看这一小节哦，上一小节中我们介绍了二叉树的遍历方式，为了测试方便，我们先补充一个层序遍历的二叉树创建方式，我们希望根据给出的列表，例如【1，2，3，4，5，6】就创建出如下图所示的完全二叉树

二叉树的一些概念

• 完全二叉树：看最下面一层叶子节点，如果节点都分布在左边，并且除了叶子节点以外的层的节点个数为2^(n-1)个，那么这颗二叉树为满二叉树
• 满二叉树：每层节点的个数为2^(n-1)个
• 叶子节点，没有左节点和右节点的节点被称为叶子节点，也就是最后一层节点

• 先来理清一下思路，如果要通过一个列表来构造完全二叉树，首先是不是得确认我们要构造几层？这个很简单，对于【1，2，3，4，5，6】这个列表来说，第一层最多1个，第二层最多2个，第四层最多4个，对于六个节点的二叉树，我们只需要构造三层即可
• 除了理清层数以外，是不是还得链接层与层之间的节点，例如1.left=2，1.right=3这样的代码是必不可少的，当我们在处理第二层的节点时，是不是需要拿出之前已经处理过的节点进行连接 ，所以我们需要一个容器
• 在介绍层序遍历的时候我们用到了一个叫队列的容器，它是先进先出的（像一根管子一样，append接口从尾部添加元素，popleft接口从头部取出元素），它在这里是不是也同样适用呢，可以思考一下
• 反过来看第一点，是否一定要通过节点个数来确认构造层数呢，因为我们使用了容器来存储节点，在容器内没有节点的时候，代码是否会自动判断不应该继续往下构造了呢？
• 假如我们要根据列表构造任意二叉树呢，那是否要对列表中的值进行判断，如果为None就不继续往下构造了

带着这些思考我们写出创建二叉树的代码：

import collections #别忘记导入容器工具
class TreeNode:
    def __init__(self, val=0, left=None,right=None):
        self.val = val
        self.left = left
        self.right = right
        
    @staticmethod
    def levelOrder(root):
        if root == None: return [] # 特判
        que = collections.deque([root]) # 双端队列，初始化并且将root丢进队列
        ans = []
        while len(que) != 0:
            size = len(que)
            level = []
            for _ in range(size): # 遍历当前层节点
                cur = que.popleft() # 从左边弹出队列
                level.append(cur.val) # 将当前节点值加入当前层的列表
                if cur.left != None: que.append(cur.left)
                if cur.right != None: que.append(cur.right)
            ans.append(level) # 将当前层结果加入答案列表
        return ans
    
    @staticmethod
    def create(list):
        que = collections.deque()
        #如果列表中节点小于1返回空
        if(len(list)<1):return None
        #创建根节点放入队列中
        root=TreeNode(list[0])
        que.append(root)
        #根据索引创建节点
        idx = 1
        while (que):
            #拿到上一层的节点
            curNode=que.popleft()
            #如果索引越界直接退出循环
            if(idx>len(list)-1):break
            #若当前值不为None
            if[list[idx]]:
                leftNode=TreeNode(list[idx])
            #连接左节点
                curNode.left=leftNode
            #添加左节点进入容器
                que.append(leftNode)
            #idx自增
            idx+=1
            
            
            #如果索引越界直接退出循环
            if(idx>len(list)-1):break
                
            if[list[idx]]:
                rightNode=TreeNode(list[idx])
            #连接右节点
                curNode.right=rightNode
            #添加左节点进入容器
                que.append(rightNode)
            #idx自增
            idx+=1
        return root

    @staticmethod
    def printList(list):
        for subList in list:
            print(subList)

tree=TreeNode.create([0,1,2,None,4,None,6,7])
TreeNode.printList(TreeNode.levelOrder(tree))
print("-------")
tree2=TreeNode.create([1,2,3,4,5,6])
TreeNode.printList(TreeNode.levelOrder(tree2))

以上代码的打印结果如下：

[0]
[1, 2]
[None, 4, None, 6]
[7]
-------
[1]
[2, 3]
[4, 5, 6]

以下开始才是正片

二叉树的最大深度

题目链接

做二叉树的题目需要把目光聚焦在当前节点应该做什么，比方说对于这道题，我们的目标是计算二叉树的最大高度，对于每个节点来说，我们是不是需要把下一层中拿到的高度加1并且返回，为什么是下一层而不是上一层，由于递归的特性，我们会先到达二叉树的底部，再开始往上走，好好体会一下这句话，最终我们在最上层来决定哪个高度才是我们需要的

因为这是二叉树的第一题，所以这里给一下代码框架

root定义为二叉树的根节点
int maxDepth(root){
    //首先要判断根节点为空会发生什么
    //由于递归函数的存在，这句话同时也是递归的停止条件
    if(root==null){
        //我们这里最终返回的是高度，想象如果没有节点该返回啥？
    }else{
        //如果不为空，是不是要计算高度了
        //写递归代码的诀窍在于，默认当前的函数已经能计算出我们需要的结果了
        left_height=当前节点左子树的高度
        right_height=当前节点右子树的高度
        //想一下返回值是什么？
        //是不是就是左子树和右子树较大的那个加上当前节点的层数？
        
    }
}

 代码如下：

class Solution:
    def maxDepth(self, root):
        if root is None: 
            return 0 
        else: 
            left_height = self.maxDepth(root.left) 
            right_height = self.maxDepth(root.right) 
            return max(left_height, right_height) + 1

solve=Solution()
tree=TreeNode.create([0,1,2,None,4,None,6,7])
print(solve.maxDepth(tree))#打印4
tree2=TreeNode.create([1,2,3,4,5,6])
print(solve.maxDepth(tree2))#打印3

使用好递归函数的关键在于，默认当前的函数已经具备了完整的解决问题的能力：

对于此题，在else条件里，我们是不是认为maxDepth函数已经可以返回左子树和右子树的 最大值了，因此才能写出这样的代码，好好体会一下吧

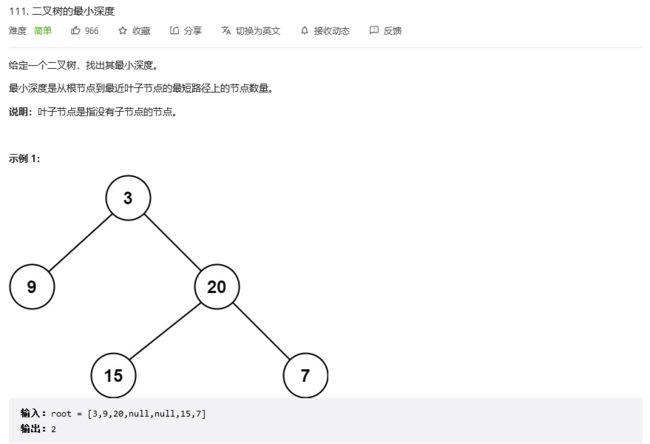
 二叉树的最小深度

题目链接

 题目很类似，对于上一题，这次返回的是最小的深度，是不是觉得很类似，你可能会想当然的写出如下代码，但是这样的代码对于一些特殊情况是无法处理的,比如【1，2】这个用例，我们打印出来是1，而不是2：

class Solution:
    def minDepth(self, root):
        if root is None: 
            return 0 
        else: 
            left_height = self.minDepth(root.left) 
            right_height = self.minDepth(root.right) 
            return min(left_height, right_height) + 1

solve=Solution()
tree=TreeNode.create([1,2])
TreeNode.printList(TreeNode.levelOrder(tree))
print(solve.minDepth(tree))#打印1

这道题的关键在于搞清楚递归结束的条件：

• 当root的左右节点都为空，那是否说明root为叶子节点，此时才应该返回值1
• 当root的左右节点右一个为空的时候，我们应该返回不为空的那个节点的深度
• 当root的左右孩子节点都不为空的时候，我们应返回左右孩子中较小的深度的节点值

我们上述代码不对的原因，对于【1，2】这个算例来说，就是没有识别出叶子节点，我们仅仅返回了两个深度中较为小的那个深度

正确的代码应该是下面这样的：

class Solution:
    def minDepth(self, root: TreeNode):
        '''
        叶子节点的定义是左孩子和右孩子都为 null 时叫做叶子节点
        1. 当 root 节点左右孩子都为空时，返回 1
        2. 当 root 节点左右孩子有一个为空时，返回不为空的孩子节点的深度
        3. 当 root 节点左右孩子都不为空时，返回左右孩子较小深度的节点值
        '''
        if not root:
            return 0

        left_min = self.minDepth(root.left)
        right_min = self.minDepth(root.right)
        
        if not root.left and not root.right: # 情况 1
            return 1
        elif not root.left or not root.right: # 情况 2
            return left_min + 1 if root.left else right_min + 1
        else: # 情况 3
            return min(left_min, right_min) + 1

solve=Solution()
tree=TreeNode.create([1,2])
TreeNode.printList(TreeNode.levelOrder(tree))
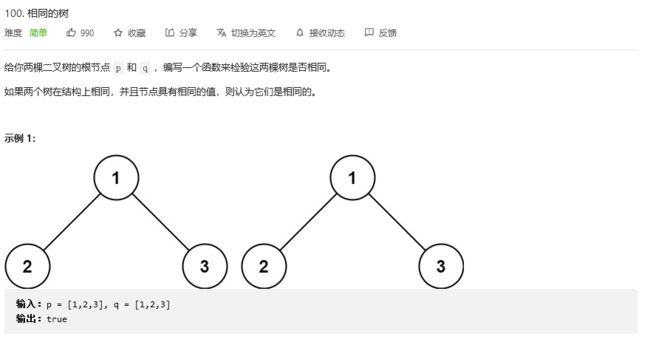
print(solve.minDepth(tree))#打印2

相同的树

题目链接

题目给出两个树，让我们判断是否相同，因为我们之前说了二叉树的遍历方式，我们是不是只要按照相同的遍历方式去把两个二叉树的列表打印出来，再比较列表的项是否相同就可以了呢？这样的方式是可行的，可是如果两颗二叉树一开始就不同，那早就可以退出函数返回false了，现在却还要遍历完整个二叉树，这样的话效率是不是就变低了，所以还是得使用递归的方式求解

还是那句话，预设我们的函数已经能完整的回答问题了，然后弄清楚每个节点应该干什么:

• 如果q节点为空，p节点为空要返回什么
• 如果p和q中一个节点为空要返回什么
• 如果p和q的val值不同该怎么办
• 递归到整个树过程中应该如何（当前节点可以从左子树和右子树中获得什么结果）

class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        if not p and not q:
            return True
        elif not p or not q:
            return False
        elif p.val != q.val:
            return False
        else:
            return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

solve=Solution()
tree=TreeNode.create([1,2,4,4,5,6])
tree2=TreeNode.create([1,2,3,4,5,6])
print(solve.isSameTree(tree,tree2))#false

课外作业

这里还有一些这个阶段可以完成的二叉树作业哦：

对称二叉树：判断一个二叉树是否对称，是不是和判断两个二叉树是否相同有点类似嘞

平衡二叉树：判断一个二叉树是否平衡，意思是左子树的高度和右子树的高度不能超过1

路径总和：判断能否找到从根节点到叶子节点累加后的值刚好等于给出的值这样的情况