TensorFlow学习笔记(一)
一、如何在Ubuntu上编辑和运行TensorFlow包下的代码
(1)使用vim编辑器编辑,终端运行代码
该方法首先需要打开Ubuntu的终端,然后输入以下代码进入Anaconda管理下安装了TensorFlow包的Python环境:
zlt@zlt-virtual-machine:~/download/MyTfTest$ source activate tensorflow
![]()
成功运行后即可在前面看到括号里面有tensorflow,便进入成功了。
接下来可以使用vim编辑器来编辑Python代码:
(tensorflow) zlt@zlt-virtual-machine:~/download/MyTfTest$ vim TfTest3.py
![]()
进入后,即可使用vim编辑器编辑Python代码:

接下来就可以使用python + Python文件名来运行Python代码了:
python TfTest3.py
结果如下:

(2)使用Visual Studio Code编辑和运行代码
我是在Ubuntu上面的软件商城来安装VS Code的,安装过程很简单,而且VS Code上面下载的插件可以帮我们配置我自己的Python环境,包括Ubuntu自带的Python环境和我安装的Anaconda管理的两个Python环境,而且切换这些环境的操作非常简单,只需要简单的操作就行:


并且,VS Code还可以帮我们自动在终端写代码,我们只需要点击运行按钮即可,非常方便。

以下是我在VS Code下载的插件:

这些插件帮我做了很多事情,不仅仅只是帮我配置环境那么简单,还有一些可以优化VS Code编辑代码的字体、亮度等等。
总的来说,虽然VS Code十分方便,但它本质上没办法锻炼我们在Linux环境下的开发,如果有能力还是尽量在终端来运行。
二、概述
一、 基本概念
1、什么是人工智能
人工智能的概念:机器模拟人的意识和思维
重要人物:艾伦·麦席森·图灵(Alan Mathison Turing)
人物简介:1912年6月23日-1954年6月7日,英国数学家、逻辑学家,被称为计算机科学之父,人工智能之父。
相关事件:
(1)1950年在论文《机器能思考吗?》中提出了图灵测试,一种用于判定机器是否具有智能的试验方法:提问者和回答者隔开,提问者通过一些装置(如键盘)向机器随意提问。多次测试,如果有超过30%的提问者认为回答问题的是人而不是机器,那么这台机器就通过测试,具有了人工智能。也就是工智能的概念:“用机器模拟人的意识和思维”。
(2)图灵在论文中预测:在2000年,会出现通过图灵测试具备人工智能的机器。然而直到2014年6月,英国雷丁大学的聊天程序才成功冒充了13岁男孩,通过了图灵测试。这一事件比图灵的预测晚了14年。
(3)在2015年11月 science杂志封面新闻报道,机器人已经可以依据从未见过的文字中的一个字符,写出同样风格的字符,说明机器已经具备了迅速学习陌生文字的创造能力。
消费级人工智能产品:
国外:
(1)谷歌Assistant
(2)微软Cortana
(3)苹果Siri
(4)亚马逊Alexa
国内:
(1)阿里的天猫精灵
(2)小米的小爱同学
人工智能先锋:
(1)GeoffreyHinton:多伦多大学的教授,谷歌大脑多伦多分
布负责人,是人工智能领域的鼻祖,他发表了许多让神经网络得以应用的论文,激活了整个人工智能领域。他还培养了许多人工智能的大家。比如LeCun就是他的博士后。
(2)Yann LeCun:纽约大学的教授,Facebook人工智能研究室负责人,他改进
了卷积神经网路算法,使卷积神经网络具有了工程应用价值,现在卷积神经网络依旧是计算机视觉领域最有效的模型之一。
(3)Yoshua Bengio:蒙特利尔大学的教授,现任微软公司战略顾问,他推动了循环神经网路算法的发展,使循环神经网络得到工程应用,用循环神经网络解决了自然语言处理中的问题。
2、什么是机器学习
机器学习的概念:机器学习是一种统计学方法,计算机利用已有数据得出某种模型,再利用此模型预测结果。

特点:随经验的增加,效果会变好。
简单模型举例:决策树模型
预测班车到达时间问题描述: 每天早上七点半,班车从A地发往B地,到达B 地的时间如何准确预测?
如果你第一次乘坐班车,你的预测通常不太准。一周之后,你大概能预测出班车 8:00左右到达B地;一个月之后,随着经验的增加,你还会知道,周一常堵车,会晚10分钟,下雨常堵车,会晚20分钟。于是你画出了如下的一张树状图,如果是周一,还下了雨,班车会8:30到达;如果不是周一,也没有下雨,班车会8:00到达。
传统计算机是基于冯诺依曼结构,指令预先存储。
运行时,CPU从存储器里逐行读取指令,按部就班逐行执行预先安排好的指令。
其特点是,输出结果确定,因为先干什么,后干什么都已经提前写在指令里了。

机器学习三要素:数据、算法、算力
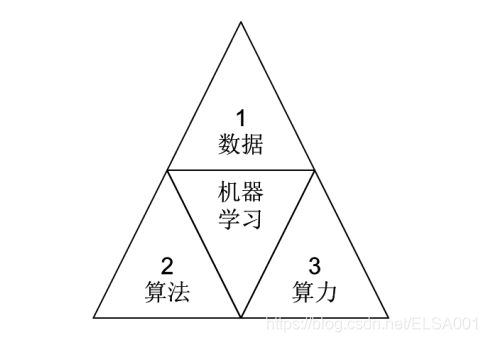
3、什么是深度学习
深度学习的概念:深层次神经网络,源于对生物脑神经元结构的研究。
人脑神经网络:随着人的成长,脑神经网络是在渐渐变粗变壮。

生物学中的神经元:下图左侧有许多支流汇总在一起,生物学中称这些支流叫做树突。树突具有接受刺激并将冲动传入细胞体的功能,是神经元的输入。这些树突汇总于细胞核又沿着一条轴突输出。轴突的主要功能是将神经冲动由胞体传至其他神经元,是神经元的输出。人脑便是由860亿个这样的神经元组成,所有的思维意识,都以它为基本单元,连接成网络实现的。

计算机中的神经元模型:1943年,心理学家McCulloch和数学家Pitts参考了生物神经元的结构,发表了抽象的神经元模型MP。神经元模型是一个包含输入,输出与计算功能的模型。输入可以类比为神经元的树突,输出可以类比为神经元的轴突,计算可以类比为细胞核。

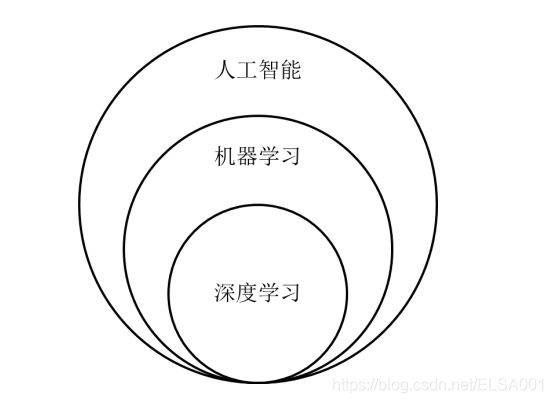
4、人工智能 Vs 机器学习 Vs 深度学习
人工智能,就是用机器模拟人的意识和思维。
机器学习,则是实现人工智能的一种方法,是人工智能的子集。
深度学习,就是深层次神经网络,是机器学习的一种实现方法,是机器学习的子集。
二、 神经网络的发展历史(三起两落)
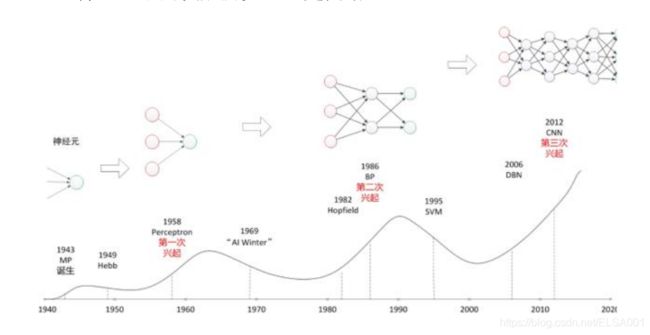
第一次兴起:1958年,人们把两层神经元首尾相接,组成单层神经网络,称做感知机。感知机成了首个可以学习的人工神经网络。引发了神经网络研究的第一次兴起。
第一次寒冬:1969年,这个领域的权威学者 Minsky 用数学公式证明了只有单层神经网络的感知机无法对异或逻辑进行分类,Minsky 还指出要想解决异或可分问题,需要把单层神经网络扩展到两层或者以上。然而在那个年代计算机的运算能力,是无法支撑这种运算量的。只有一层计算单元的感知机,暴露出他的天然缺陷,使得神经网络研究进入了第一个寒冬。
第二次兴起:1986年,Hinton等人提出了反向传播方法,有效解决了两层神经网络的算力问题。引发了神经网络研究的第二次兴起。
第二次寒冬:1995年,支持向量机诞生。支持向量机可以免去神经网络需要调节参数的不足,还避免了神经网络中局部最优的问题。一举击败神经网络,成为当时人工智能领域的主流算法,使得神经网络进入了他的第二个冬季。
第三次兴起:2006年,深层次神经网络出现,2012年,卷积神经网络在图像识别领域中的惊人表现,又引发了神经网络研究的再一次兴起。
三、 机器学习的典型应用
1、 应用领域计算机视觉、语音识别、自然语言处理
2、主流应用:
(1) 预测(对连续数据进行预测)如,预测某小区100平米的房价卖多少钱。 根据以往数据(红色),拟合出一条线,让它“穿过”所有的点,并且与各个点的距离尽可能的小。
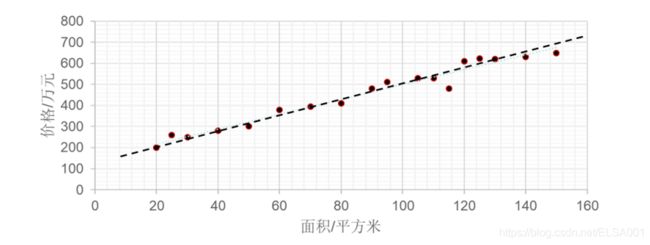
我们可以把以前的数据,输入神经网络,让他训练出一个模型,比如这张图中红色点表示了以往的数据,虚线表示了预测出的模型Y = ax + b ,大量历史数据也就是面积x 和房价y作为输入,训练出了模型的参数a= 3.5, b = 150,则你家100平米的房价应该是3.5 * 100 + 150 = 500万。
我们发现,模型不一定全是直线,也可以是曲线;我们还发现,随着数据的增多,模型一般会更准确。(2) 分类(对离散数据进行分类) 如,根据肿瘤患者的年龄和肿瘤大小判断良性、恶性。
红色样本为恶性,蓝色样本为良性,绿色分为哪类?

假如让计算机判断肿瘤是良性还是恶性,先要把历史数据输入到神经网络进行建模,调节模型的参数,得到一条线把良性肿瘤和恶性肿瘤分开。比如输入患者的年龄、肿瘤的大小还有对应的良性肿瘤还是恶性肿瘤,使用神经网络训练模型 调整参数,再输入新的患者年龄和肿瘤大小时,计算机会直接告诉你肿瘤是良性还是恶性。比如上图的绿色三角就属于良性肿瘤。
四、课程小结
1、机器学习,就是在任务T上,随经验E的增加,效果P随之增加。
2、机器学习的过程是通过大量数据的输入,生成一个模型,再利用这个生成的模型,实现对结果的预测。
3、庞大的神经网络是基于神经元结构的,是输入乘以权重,再求和,再过非线性函数的过程。
三、Python语法
常用基础语法点
# linux :
# pwd
# ls
# mkdir
# touch
# cd + dir
# python
print("hello world")
print(5 + 3 * 2)
a = 100
b = "hello world"
print("point = %s \n %s" %(a,b) )
列表、元组、字典
c = [1,2,3,4,5,6,7]
d = ["Elsa","zlt","hhh"]
e = [1,2,3,4,5,"d"]
# [1, 3, 5, 7]
print(c[0::2])
# [7, 4, 1]
print(c[-1::-3])
c.insert(3,38)
# [1, 2, 3, 38, 4, 5, 6, 7]
print(c)
del c[3]
# [1, 2, 3, 4, 5, 6, 7]
print(c)
f = (1,2,3)
print(f)
# key:value
dic = {1:"123","name":"Elsa","height":180}
# 180
print(dic["height"])
dic["height"] = 175
# 175
print(dic["height"])
del dic["name"]
# {1: '123', 'height': 175}
print(dic)
dic["age"] = 18
# {1: '123', 'height': 175, 'age': 18}
print(dic)
条件语句
age = input("input your age\n")
if(age > "18"):
print("more than 18 year-old")
else:
print("less than or equal 18 year-old")
# input your age
# 99
# more than 18 year-old
逻辑关系
num = input("please input your class number:")
if num == "1" or num == "2":
print("class room 302")
elif num == "3":
print("class room 303")
elif num == "4":
print("class room 304")
else:
print("class room 305")
# please input your class number:4
# class room 304
循环语句
# hello world
# hello world
# hello world
# hello world
# hello world
for i in range(0,5):
print("hello world")
# hello world 0
# hello world 1
# hello world 2
# hello world 3
# hello world 4
for i in range(0,5):
print("hello world %s" %(i))
# a
# a
# b
# c
# d
# b
# a
# b
# c
# d
# c
# a
# b
# c
# d
# d
# a
# b
# c
# d
h = ["a","b","c","d"]
for i in h:
print(i)
for j in h:
print(j)
# 2 3
# 3 4
# 4 5
x = 1
y = 2
while x < 5 and y < 5:
x = x + 1
y = y + 1
print(x,y)
turtle模块
import turtle
t = turtle.Pen()
t.forward(100)
t.left(90)
t.forward(100)
t.left(90)
t.forward(100)
t.left(90)
t.forward(100)
t.left(90)
for i in range(0,4):
t.forward(100)
t.left(90)
t.reset()
i = 0
while True:
t.forward(100)
t.left(90)
i = i + 1
if i == 8:
break
函数、模块、包
def hi_name(name):
print("hello %s" %name)
# hello Elsa
hi_name("Elsa")
def add(a,b):
return a + b
c = add(5,6)
# 11
print(c)
# 10
print(abs(-10))
import time
# Wed Jul 28 16:46:27 2021
print(time.asctime())
# from PIL import Image
class Animals():
def breathe(self):
print("breathing")
def move(self):
print("moving")
def eat(self):
print("eating food")
class Mammals(Animals):
def breastfeed(self):
print("feeding young")
class Cats(Mammals):
def __init__(self,spots):
self.spots = spots
def catch_mouse(self):
print("catch mouse")
def left_foot_forward(self):
print("left foot forward")
def left_foot_backback(self):
print("left foot backback")
def dance(self):
self.left_foot_forward()
self.left_foot_backback()
self.left_foot_forward()
self.left_foot_backback()
kitty = Cats(10)
# left foot forward
# left foot backback
# left foot forward
# left foot backback
# feeding young
# moving
print(kitty.spots)
kitty.dance()
kitty.breastfeed()
kitty.move()
文件操作
import pickle
game_data = {
"position" : "N2 E3",
"pocket" : ["key","knife"],
"money" : 160
}
save_file = open("save.dat","wb")
pickle.dump(game_data,save_file)
save_file.close()
import pickle
load_file = open("save.dat","rb")
load_game_data = pickle.load(load_file)
load_file.close()
# {'position': 'N2 E3', 'pocket': ['key', 'knife'], 'money': 160}
print(load_game_data)
四、TensorFlow框架
张量、计算图、会话
一、基本概念
基于Tensorflow的NN:用张量表示数据,用计算图搭建神经网络,用会话执行计算图,优化线上的权重(参数),得到模型。
张量:张量就是多维数组(列表),用“阶”表示张量的维度。
0阶张量称作标量,表示一个单独的数;
举例 S=123
1阶张量称作向量,表示一个一维数组;
举例 V=[1,2,3]
2阶张量称作矩阵,表示一个二维数组,它可以有i行j列个元素,每个元素可以用行号和列号共同索引到;
举例 m=[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
判断张量是几阶的,就通过张量右边的方括号数,0个是0阶,n个是n阶,张量可以表示0阶到n阶数组(列表);
举例 t=[ [ [… ] ] ]为3阶。
数据类型:Tensorflow的数据类型有tf.float32、tf.int32等。
举例
我们实现Tensorflow的加法:
# 引入模块
import tensorflow as tf
# 定义一个张量等于[1.0,2.0]
a = tf.constant([1.0,2.0])
# 定义一个张量等于[3.0,4.0]
b = tf.constant([3.0,4.0])
# 实现a加b的加法
result = a + b
# 打印出结果 可以打印出这样一句话:
# Tensor(“add:0”, shape=(2, ), dtype=float32)
# 意思为result是一个名称为add:0的张量,
# shape=(2,)表示一维数组长度为2,
# type=float32表示数据类型为浮点型。
print(result)
计算图(Graph):搭建神经网络的计算过程,是承载一个或多个计算节点的一张图,只搭建网络,不运算。
举例
在第一讲中我们曾提到过,神经网络的基本模型是神经元,神经元的基本模型其实就是数学中的乘、加运算。
我们搭建如下的计算图:

x1、x2表示输入,w1、w2分别是x1到y和x2到y的权重,y=x1w1+x2w2。
我们实现上述计算图:
# 引入模块
import tensorflow as tf
# 定义一个2阶张量等于[[1.0,2.0]]
x = tf.constant([[1.0, 2.0]])
#定义一个2阶张量等于[[3.0],[4.0]]
w = tf.constant([[3.0], [4.0]])
# 实现xw矩阵乘法
y=tf.matmul(x,w)
# 打印出结果 可以打印出这样一句话:Tensor(“matmul:0”, shape(1,1), dtype=float32),
print(y)
# 执行会话并打印出执行后的结果
# 可以打印出这样的结果:[[11.]]
with tf.Session() as sess:
print(sess.run(y))
从这里我们可以看出,print的结果显示y是一个张量,只搭建承载计算过程的计算图,并没有运算,如果我们想得到运算结果就要用到“会话Session()”了。
会话(Session):执行计算图中的节点运算。我们用with结构实现,语法如下:
with tf.Session() as sess:
print sess.run(y)
上面代码会话后打印出了y的结果1.03.0+ 2.04.0 = 11.0。
注意:
①:我们以后会常用到vim编辑器,为了使用方便,我们可以更改vim的配置文件,使vim的使用更加便捷。
我们在vim~/.vimrc 写入:
set ts=4 表示使Tab键等效为4个空格
set nu 表示使vim显示行号 nu是number缩写
②:在vim编辑器中运行Session()会话时,有时会出现“提示warning”,是因为有的电脑可以支持加速指令,但是运行代码时并没有启动这些指令。可以把这些“提示warning”暂时屏蔽掉。屏蔽方法为进入主目录下的bashrc文件,在bashrc 文件中加入这样一句 export TF_CPP_MIN_LOG_LEVEL=2,从而把“提示 warning”等级降低。source 命令用于重新执行修改的初始化文件,使之立即生效,而不必注销并重新登录。
vim ~/.bashrc
source ~/.bashrc
前向传播
神经网络的参数
神经网络的参数:是指神经元线上的权重w,用变量表示,一般会先随机生成这些参数。
生成参数的方法是让w等于tf.Variable,把生成的方式写在括号里。 神经网络中常用的生成随机数/数组的函数有:
tf.random_normal() 生成正态分布随机数
tf.truncated_normal() 生成去掉过大偏离点的正态分布随机数
tf.random_uniform() 生成均匀分布随机数
tf.zeros 表示生成全0数组
tf.ones 表示生成全1数组
tf.fill 表示生成全定值数组
tf.constant 表示生成直接给定值的数组
举例
① w=tf.Variable(tf.random_normal([2,3],stddev=2, mean=0, seed=1))
表示生成正态分布随机数,形状两行三列,标准差是2,均值是0,随机种子是1。
② w=tf.Variable(tf.Truncated_normal([2,3],stddev=2, mean=0, seed=1)),
表示去掉偏离过大的正态分布,也就是如果随机出来的数据偏离平均值超过两个标准差,这个数据将重新生成。
③ w=random_uniform(shape=7,minval=0,maxval=1,dtype=tf.int32,seed=1),
表示从一个均匀分布[minval maxval)中随机采样,注意定义域是左闭右开,即包含minval,不包含maxval。
④ 除了生成随机数,还可以生成常量。
tf.zeros([3,2],int32)表示生成[[0,0],[0,0],[0,0]];
tf.ones([3,2],int32)表示生成[[1,1],[1,1],[1,1];
tf.fill([3,2],6)表示生成[[6,6],[6,6],[6,6]];
tf.constant([3,2,1])表示生成[3,2,1]。
注意:
①随机种子如果去掉每次生成的随机数将不一致。
②如果没有特殊要求标准差、均值、随机种子是可以不写的。
神经网络的搭建
当我们知道张量、计算图、会话和参数后,我们可以讨论神经网络的实现过程了。
神经网络的实现过程:
1、准备数据集,提取特征,作为输入喂给神经网络(Neural Network,NN)
2、搭建NN结构,从输入到输出(先搭建计算图,再用会话执行)
( NN前向传播算法 -----> 计算输出)
3、大量特征数据喂给NN,迭代优化NN参数
( NN反向传播算法 -----> 优化参数训练模型)
4、使用训练好的模型预测和分类
由此可见,基于神经网络的机器学习主要分为两个过程,即训练过程和使用过程。
训练过程是第一步、第二步、第三步的循环迭代,使用过程是第四步,一旦参数优化完成就可以固定这些参数,实现特定应用了。很多实际应用中,我们会先使用现有的成熟网络结构,喂入新的数据,训练相应模型,判断是否能对喂入的从未见过的新数据作出正确响应,再适当更改网络结构,反复迭代,让机器自动训练参数找出最优结构和参数,以固定专用模型。
前向传播
前向传播就是搭建模型的计算过程,让模型具有推理能力,可以针对一组输入给出相应的输出。
举例
假如生产一批零件,体积为x1,重量为x2,体积和重量就是我们选择的特征,把它们喂入神经网络,当体积和重量这组数据走过神经网络后会得到一个输出。
假如输入的特征值是:体积0.7 重量0.5
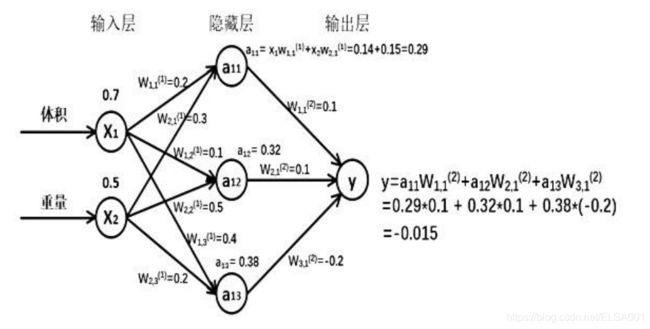
由搭建的神经网络可得,隐藏层节点a11=x1w11+x2w21=0.14+0.15=0.29,同理算得节点a12=0.32,a13=0.38,最终计算得到输出层Y=-0.015,这便实现了前向传播过程。
推导:
第一层 X是输入为1X2矩阵 用x表示输入,是一个1行2列矩阵,表示一次输入一组特征,这组特征包含了 体积和重量两个元素。
W 前节点编号,后节点编号(层数) 为待优化的参数
对于第一层的w 前面有两个节点,后面有三个节点 w应该是个两行三列矩阵,
我们这样表示:
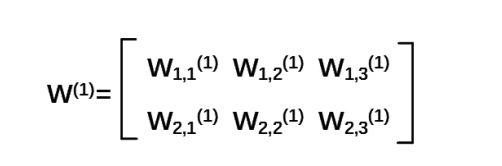
神经网络共有几层(或当前是第几层网络)都是指的计算层,输入不是计算层,所以a为第一层网络,a是一个一行三列矩阵。
我们这样表示:a(1)=[a11, a12, a13]=XW(1)
第二层参数要满足前面三个节点,后面一个节点,所以W(2) 是三行一列矩阵。 我们这样表示:
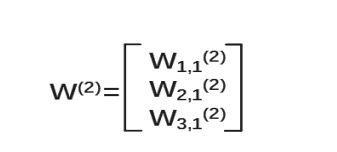
我们把每层输入乘以线上的权重w,这样用矩阵乘法可以计算出输出y了。
a= tf.matmul(X,W1)
y= tf.matmul(a, W2)
由于需要计算结果,就要用with结构实现,所有变量初始化过程、计算过程都要放到 sess.run 函数中。
对于变量初始化,我们在sess.run中写入tf.global_variables_initializer实现对所有变量初始化,也就是赋初值。对于计算图中的运算,我们直接把运算节点填入sess.run 即可,比如要计算输出y,直接写 sess.run(y) 即可。
在实际应用中,我们可以一次喂入一组或多组输入,让神经网络计算输出y,可以先用tf.placeholder给输入占位。
如果一次喂一组数据shape的第一维位置写1,第二维位置看有几个输入特征;
如果一次想喂多组数据,shape的第一维位置可以写None表示先空着,第二维位置写有几个输入特征。
这样在feed_dict中可以喂入若干组体积重量了。
举例 这是一个实现神经网络前向传播过程,网络可以自动推理出输出y的值。
①用placeholder实现输入定义(sess.run中喂入一组数据)的情况 第一组喂体积0.7、重量0.5
# 两层简单神经网络(全连接)
import tensorflow as tf
# 定义输入和参数
# 用placeholder实现输入定义 (sess.run中喂一组数据)
x = tf.placeholder(tf.float32, shape=(1, 2))
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
# 定义前向传播过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
# 用会话计算结果
# y in tf3_4.py is:
# [[3.0904665]]
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
print("y in tf3_4.py is:\n",sess.run(y, feed_dict={x: [[0.7,0.5]]}))
②用placeholder实现输入定义(sess.run中喂入多组数据)的情况第一组喂体积0.7、重量0.5,第二组喂体积0.2、重量0.3,第三组喂体积0.3 、重量0.4,第四组喂体积0.4、重量0.5.
# 两层简单神经网络(全连接)
import tensorflow as tf
# 定义输入和参数
# 用placeholder定义输入(sess.run喂多组数据)
x = tf.placeholder(tf.float32, shape=(None, 2))
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
# 定义前向传播过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
# 调用会话计算结果
# the result of tf3_5.py is:
# [[3.0904665]
# [1.2236414]
# [1.7270732]
# [2.2305048]]
# w1:
# [[-0.8113182 1.4845988 0.06532937]
# [-2.4427042 0.0992484 0.5912243 ]]
# w2:
# [[-0.8113182 ]
# [ 1.4845988 ]
# [ 0.06532937]]
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
print("the result of tf3_5.py is:\n",sess.run(y, feed_dict={x: [[0.7,0.5],[0.2,0.3],[0.3,0.4],[0.4,0.5]]}))
print("w1:\n", sess.run(w1))
print("w2:\n", sess.run(w2))
反向传播
反向传播:训练模型参数,在所有参数上用梯度下降,使NN模型在训练数据上的损失函数最小。
损失函数(loss):计算得到的预测值y与已知答案y_的差距。
损失函数的计算有很多方法,均方误差MSE是比较常用的方法之一。
均方误差MSE:求前向传播计算结果与已知答案之差的平方再求平均。

用tensorflow函数表示为:
loss_mse =tf.reduce_mean(tf.square(y_ - y))
反向传播训练方法:
以减小loss值为优化目标,有梯度下降、momentum优化器、adam优化器等优化方法。
这三种优化方法用tensorflow的函数可以表示为:
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
train_step=tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss)
train_step=tf.train.AdamOptimizer(learning_rate).minimize(loss)
三种优化方法区别如下:
①tf.train.GradientDescentOptimizer()
使用随机梯度下降算法,使参数沿着梯度的反方向,即总损失减小的方向移动,实现更新参数。
②tf.train.MomentumOptimizer()
在更新参数时,利用了超参数,实现更新参数。
③tf.train.AdamOptimizer()
是利用自适应学习率的优化算法,Adam 算法和随机梯度下降算法不同。随机梯度下降算法保持单一的学习率更新所有的参数,学习率在训练过程中并不会改变。而 Adam 算法通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。 学习率:决定每次参数更新的幅度。优化器中都需要一个叫做学习率的参数,使用时,如果学习率选择过大会出现震荡不收敛的情况,如果学习率选择过小,会出现收敛速度慢的情况。我们可以选个比较小的值填入,比如0.01、0.001。
搭建神经网络的八股
我们最后梳理出神经网络搭建的八股,神经网络的搭建课分四步完成:准备工作、前向传播、反向传播和循环迭代。
0.导入模块,生成模拟数据集
import
常量定义
生成数据集
1.前向传播:定义输入、参数和输出
x= y_=
w1= w2=
a= y=
2. 反向传播:定义损失函数、反向传播方法
loss=
train_step=
3. 生成会话,训练STEPS轮
with tf.session() as sess
Init_op=tf. global_variables_initializer()
sess_run(init_op)
STEPS=3000 for i in range(STEPS):
start= end=
sess.run(train_step, feed_dict:)
举例
随机产生32组生产出的零件的体积和重量,训练3000轮,每500轮输出一次损失函数。
# 0.导入模块,生成模拟数据集。
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
# 基于seed产生随机数
rdm = np.random.RandomState(SEED)
# 随机数返回32行2列的矩阵 表示32组 体积和重量 作为输入数据集
X = rdm.rand(32,2)
# 从X这个32行2列的矩阵中 取出一行 判断如果和小于1 给Y赋值1 如果和不小于1 给Y赋值0
# 作为输入数据集的标签(正确答案)
Y_ = [[int(x0 + x1 < 1)] for (x0, x1) in X]
print("X:\n",X)
print("Y_:\n",Y_)
# 1.定义神经网络的输入、参数和输出,定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_= tf.placeholder(tf.float32, shape=(None, 1))
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
# 2.定义损失函数及反向传播方法。
loss_mse = tf.reduce_mean(tf.square(y-y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)
# train_step = tf.train.MomentumOptimizer(0.001,0.9).minimize(loss_mse)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss_mse)
# 3.生成会话,训练STEPS轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
# 输出目前(未经训练)的参数取值。
print("w1:\n", sess.run(w1))
print("w2:\n", sess.run(w2))
print("\n")
# 训练模型。
STEPS = 3000
for i in range(STEPS):
start = (i*BATCH_SIZE) % 32
end = start + BATCH_SIZE
sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
if i % 500 == 0:
total_loss = sess.run(loss_mse, feed_dict={x: X, y_: Y_})
print("After %d training step(s), loss_mse on all data is %g" % (i, total_loss))
# 输出训练后的参数取值。
print("\n")
print("w1:\n", sess.run(w1))
print("w2:\n", sess.run(w2))
# X:
# [[0.83494319 0.11482951]
# [0.66899751 0.46594987]
# [0.60181666 0.58838408]
# [0.31836656 0.20502072]
# [0.87043944 0.02679395]
# [0.41539811 0.43938369]
# [0.68635684 0.24833404]
# [0.97315228 0.68541849]
# [0.03081617 0.89479913]
# [0.24665715 0.28584862]
# [0.31375667 0.47718349]
# [0.56689254 0.77079148]
# [0.7321604 0.35828963]
# [0.15724842 0.94294584]
# [0.34933722 0.84634483]
# [0.50304053 0.81299619]
# [0.23869886 0.9895604 ]
# [0.4636501 0.32531094]
# [0.36510487 0.97365522]
# [0.73350238 0.83833013]
# [0.61810158 0.12580353]
# [0.59274817 0.18779828]
# [0.87150299 0.34679501]
# [0.25883219 0.50002932]
# [0.75690948 0.83429824]
# [0.29316649 0.05646578]
# [0.10409134 0.88235166]
# [0.06727785 0.57784761]
# [0.38492705 0.48384792]
# [0.69234428 0.19687348]
# [0.42783492 0.73416985]
# [0.09696069 0.04883936]]
# Y_:
# [[1], [0], [0], [1], [1], [1], [1], [0], [1], [1], [1], [0], [0], [0], [0], [0], [0], [1], [0], [0], [1], [1], [0], [1], [0], [1], [1], [1], [1], [1], [0], [1]]
# w1:
# [[-0.8113182 1.4845988 0.06532937]
# [-2.4427042 0.0992484 0.5912243 ]]
# w2:
# [[-0.8113182 ]
# [ 1.4845988 ]
# [ 0.06532937]]
# After 0 training step(s), loss_mse on all data is 5.13118
# After 500 training step(s), loss_mse on all data is 0.429111
# After 1000 training step(s), loss_mse on all data is 0.409789
# After 1500 training step(s), loss_mse on all data is 0.399923
# After 2000 training step(s), loss_mse on all data is 0.394146
# After 2500 training step(s), loss_mse on all data is 0.390597
# w1:
# [[-0.7000663 0.9136318 0.08953571]
# [-2.3402493 -0.14641267 0.58823055]]
# w2:
# [[-0.06024267]
# [ 0.91956186]
# [-0.0682071 ]]
由神经网络的实现结果,我们可以看出,总共训练3000轮,每轮从X的数据集 和Y的标签中抽取相对应的从start开始到end结束个特征值和标签,喂入神经网络,用sess.run求出loss,每500轮打印一次loss值。经过3000轮后,我们打印出最终训练好的参数w1、w2。
这样四步就可以实现神经网络的搭建了。
