ABAQUS材料子程序学习（线性各向同性硬化塑性）

前言

记录自己学习abaqus软件umat子程序的t过程，本文主要参考了《非线性本构关系在ABAQUS中的实现》第四章和技术邻的视频课程“非线性各向同性强化弹塑性umat子程序教程”

塑性力学增量形式实现

计算过程中，体应变和体应力是弹性关系$$\Delta {\sigma }_v=K\cdot \Delta {\epsilon }_v\text{\hspace{1em}(1)}$$

$K$为体积模量，$K=\frac{E}{3(1-\nu )}$ , $\Delta {\epsilon }_v=\Delta {\epsilon }_{11}+\Delta {\epsilon }_{22}+\Delta {\epsilon }_{33}$

所以在下面的讨论中只考虑偏应力张量和偏应力张量

试应力： $${\mathbf{\sigma }}^{\mathbf{t}{\mathbf{r}}^{\prime }}(\mathbf{t})={\mathbf{\sigma }}^{\prime }(\mathbf{t})+{\mathbb{C}}^{\prime }:\mathbf{\Delta }{\mathbf{\epsilon }}^{\prime }\text{\hspace{1em}(2)}$$

viogt表记：
$$\left\{\begin{array}{c}{\sigma }_{11}^{t{r}^{\prime }}\\ {\sigma }_{22}^{t{r}^{\prime }}\\ {\sigma }_{33}^{t{r}^{\prime }}\\ {\sigma }_{12}^{t{r}^{\prime }}\\ {\sigma }_{23}^{t{r}^{\prime }}\\ {\sigma }_{13}^{t{r}^{\prime }}\end{array}\right\}=\left\{\begin{array}{c}{{\sigma }^{\prime }}_{11}(t)\\ {{\sigma }^{\prime }}_{22}(t)\\ {{\sigma }^{\prime }}_{33}(t)\\ {{\sigma }^{\prime }}_{12}(t)\\ {{\sigma }^{\prime }}_{23}(t)\\ {{\sigma }^{\prime }}_{13}(t)\end{array}\right\}+\left[\begin{array}{cccccc}2G& 0& 0& 0& 0& 0\\ 0& 2G& 0& 0& 0& 0\\ 0& 0& 2G& 0& 0& 0\\ 0& 0& 0& G& 0& 0\\ 0& 0& 0& 0& G& 0\\ 0& 0& 0& 0& 0& G\end{array}\right]\cdot \left\{\begin{array}{c}{\Delta {\epsilon }^{\prime }}_{11}(t)\\ {\Delta {\epsilon }^{\prime }}_{22}(t)\\ {\Delta {\epsilon }^{\prime }}_{33}(t)\\ {\Delta \gamma }_{12}(t)\\ {\Delta \gamma }_{23}(t)\\ {\Delta \gamma }_{13}(t)\end{array}\right\}$$
静态分析umat用的工程应变：$\left\{\begin{array}{c}{\Delta {\epsilon }^{\prime }}_{11}(t)\\ {\Delta {\epsilon }^{\prime }}_{22}(t)\\ {\Delta {\epsilon }^{\prime }}_{33}(t)\\ {\Delta \gamma }_{12}(t)\\ {\Delta \gamma }_{23}(t)\\ {\Delta \gamma }_{13}(t)\end{array}\right\}=\left\{\begin{array}{c}{\Delta {\epsilon }^{\prime }}_{11}(t)\\ {\Delta {\epsilon }^{\prime }}_{22}(t)\\ {\Delta {\epsilon }^{\prime }}_{33}(t)\\ {2\Delta {\epsilon }^{\prime }}_{12}(t)\\ {2\Delta {\epsilon }^{\prime }}_{23}(t)\\ {2\Delta {\epsilon }^{\prime }}_{13}(t)\end{array}\right\}$

Mises等效应力：

主应力形式：
$${\sigma }_e={\left\{\frac{1}{2}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2\right]\right\}}^{\frac{1}{2}}$$

偏应力形式:
$${\sigma }_e={\left[\frac{3}{2}\left({{\sigma }_{11}^{\prime }}^2+{{\sigma }_{22}^{\prime }}^2+{{\sigma }_{33}^{\prime }}^2+2{{\sigma }_{12}}^2+2{{\sigma }_{23}}^2+2{{\sigma }_{13}}^2\right)\right]}^{\frac{1}{2}}\text{\hspace{1em}(3)}$$

其中: ${\sigma }_{11}^{\prime }={\sigma }_{11}-{\sigma }_v$ ，${\sigma }_{22}^{\prime }={\sigma }_{22}-{\sigma }_v$， ${\sigma }_{33}^{\prime }={\sigma }_{33}-{\sigma }_v$； ${\sigma }_v=\frac{1}{3}\left[{\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33}\right]$

Mises等效塑性应变增量：
$$\Delta {\bar{\epsilon }}^p=\frac{\sqrt{2}}{3}{\left[{\left(\Delta {\epsilon }_1^p-\Delta {\epsilon }_2^p\right)}^2+{\left(\Delta {\epsilon }_2^p-\Delta {\epsilon }_3^p\right)}^2+{\left(\Delta {\epsilon }_3^p-\Delta {\epsilon }_1^p\right)}^2\right]}^{\frac{1}{2}}$$

线性硬化塑性$${\sigma }_y={\sigma }_{y0}+h{\bar{\epsilon }}^p\text{\hspace{1em}(4)}$$
初始屈服加上等效塑性应变乘以硬化系数。
等效塑性变形作为状态变量存在STATEV(NSTATV)中，提取 ${\bar{\epsilon }}^p$ 并计算当前的屈服应力 ${\sigma }_y$

(2)代入(3)，计算试应力的等效Mises应力${\sigma }_{Mises}^{tr}$

判断 ${\sigma }_{Mises}^{tr}$ 与 ${\sigma }_y$ 关系:

若 ${\sigma }_{Mises}^{tr}＜{\sigma }_y$ ： $\mathbf{\sigma }(\mathbf{t}+\mathbf{\Delta }\mathbf{t})={\mathbf{\sigma }}^{\mathbf{t}\mathbf{r}}(\mathbf{t})$

一致切线刚度矩阵，为弹性刚度矩阵
$$\mathbf{D}\mathbf{D}\mathbf{S}\mathbf{D}\mathbf{D}\mathbf{E}(i,j)=\left[\begin{array}{cccccc}2G+\lambda & \lambda & \lambda & 0& 0& 0\\ \lambda & 2G+\lambda & \lambda & 0& 0& 0\\ \lambda & \lambda & 2G+\lambda & 0& 0& 0\\ 0& 0& 0& G& 0& 0\\ 0& 0& 0& 0& G& 0\\ 0& 0& 0& 0& 0& G\end{array}\right]\text{\hspace{1em}(5)}$$

若 ${\sigma }_{Mises}^{tr}\ge {\sigma }_y$ ，计算新增的 $\Delta {\bar{\epsilon }}^p$

注：单轴拉伸下Mises等效应力${\sigma }_{Mises}={\left[\frac{1}{2}\left({\sigma }_{11}^2+{\sigma }_{11}^2\right)\right]}^{\frac{1}{2}}={\sigma }_{11}$
等效应变${\epsilon }_{Mises}=\frac{\sqrt{2}}{3}{\left[2{\left({\epsilon }_{11}-(-\mu {\epsilon }_{11})\right)}^2\right]}^{\frac{1}{2}}=\frac{2}{3}(1+\mu ){\epsilon }_{11}$
单轴拉伸：${\sigma }_{11}=E\cdot {\epsilon }_{11}$ → ${\sigma }_{Mises}=\frac{3E}{2(1+\mu )}\cdot {\epsilon }_{Mises}=3G\cdot {\epsilon }_{Mises}$

计算新增的 $\Delta {\bar{\epsilon }}^p$, $h$为塑性硬化系数
$${\sigma }_{Mises}^{tr}-3G\Delta {\bar{\epsilon }}^p={\sigma }_{y0}+h\cdot ({\bar{\epsilon }}^p+\Delta {\bar{\epsilon }}^p)$$
$${\sigma }_{Mises}^{tr}-h\cdot {\bar{\epsilon }}^p-{\sigma }_{y0}=(h+3G)\Delta {\bar{\epsilon }}^p$$
$$\Delta {\bar{\epsilon }}^p=\frac{{\sigma }_{Mises}^{tr}-h\cdot {\bar{\epsilon }}^p-{\sigma }_{y0}}{(h+3G)}$$
非线性硬化时 $h$ 是随等效塑性应变${\bar{\epsilon }}^p$变化的，通常利用Newton迭代法求解等效塑性应变增量$\Delta {\bar{\epsilon }}^p$

根据正交流动法则：
$$\mathbf{\Delta }{\mathbf{\epsilon }}^{\mathbf{p}}=\Delta {\bar{\epsilon }}^p\frac{3}{2}\frac{{\mathbf{\sigma }}^{\prime }}{{\sigma }_{Mises}}=\Delta {\bar{\epsilon }}^p\frac{3}{2}\frac{{\mathbf{\sigma }}^{\mathbf{t}{\mathbf{r}}^{\prime }}}{{\sigma }_{Mises}^{tr}}$$
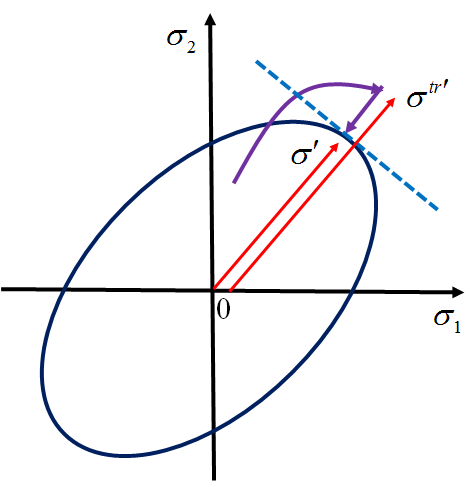
偏应力张量与试应力的偏应力张量方向相同，如下图

屈服后一致切线刚度矩阵：
应力增量=弹性刚度矩阵×弹性应变增量
$$\mathbf{d}\mathbf{\sigma }={\mathbf{D}}_{\mathbf{e}}\cdot \mathbf{d}{\mathbf{\epsilon }}^{\mathbf{e}}$$
弹性应变=总应变-塑性应变增量
$$\mathbf{d}\mathbf{\sigma }={\mathbf{D}}_{\mathbf{e}}\cdot (\mathbf{d}\mathbf{\epsilon }-\mathbf{d}{\mathbf{\epsilon }}^{\mathbf{p}})\text{\hspace{1em}(6)}$$
将 $\mathbf{d}{\mathbf{\epsilon }}^{\mathbf{p}}$ 用 $\mathbf{d}\mathbf{\epsilon }$ 表示出来，再代回式(6)就可求出屈服后的DDSDDE(NTENS,NTENS)
一致性条件
$$\{\begin{array}{l}f(\mathbf{\sigma },\overline{{\epsilon }^p})=0\\ f(\mathbf{\sigma }+d\mathbf{\sigma },\overline{{\epsilon }^p}+d\overline{{\epsilon }^p})=0\end{array}⟹\frac{\partial f}{\partial \mathbf{\sigma }}\cdot \mathbf{d}\mathbf{\sigma }+\frac{\partial f}{\partial \overline{{\epsilon }^p}}d\overline{{\epsilon }^p}=0\text{\hspace{1em}(7)}$$
屈服函数：$f(\mathbf{\sigma },\overline{{\epsilon }^p})={\sigma }_{Mises}-h\cdot \overline{{\epsilon }^p}$
$$\frac{\partial f}{\partial \mathbf{\sigma }}=\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\frac{\partial f}{\partial \overline{{\epsilon }^p}}=-h\text{\hspace{1em}(8)}$$
为了方便计算改写为矩阵形式：

用Voigt表记应力，$\mathbf{\sigma }$为列向量$[{\sigma }_{11},{\sigma }_{22},{\sigma }_{33},{\sigma }_{12},{\sigma }_{23},{\sigma }_{13}{]}^T$

因此，$\frac{\partial f}{\partial \mathbf{\sigma }}=\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}=\frac{3}{2{\sigma }_{Mises}}\left[{\sigma }_{11}^{\prime },{\sigma }_{22}^{\prime },{\sigma }_{33}^{\prime },2{\sigma }_{12}^{\prime },2{\sigma }_{23}^{\prime },2{\sigma }_{13}^{\prime }\right]$为行向量

正交条件:$$\mathbf{d}{\mathbf{\epsilon }}^{\mathbf{p}}=d\overline{{\epsilon }^p}{\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T\text{\hspace{1em}(9)}$$
(8)(9)代入(7)：
$$\begin{array}{c}d\overline{{\epsilon }^p}=\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot \frac{\mathbf{d}\mathbf{\sigma }}{h}=\frac{1}{h}\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot \mathbf{d}{\mathbf{\epsilon }}^{\mathbf{e}}\\ \\ =\frac{1}{h}\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot (\mathbf{d}\mathbf{\epsilon }-\mathbf{d}{\mathbf{\epsilon }}^{\mathbf{p}})\\ \\ =\frac{1}{h}\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}{\mathbf{D}}_{\mathbf{e}}(\mathbf{d}\mathbf{\epsilon }-d\overline{{\epsilon }^p}{\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T)\end{array}$$
$$\begin{gathered} \left\{h+\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T\right\}d\overline{{\epsilon }^p}=\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot \mathbf{d}\mathbf{\epsilon } \\ d\overline{{\epsilon }^p}=\frac{\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot \mathbf{d}\mathbf{\epsilon }}{h+\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T} \\ d{\mathbf{\epsilon }}^{\mathbf{p}}=\frac{{\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T\otimes \frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot \mathbf{d}\mathbf{\epsilon }}{h+\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T} \end{gathered}$$
代入(6):
$$\mathbf{d}\mathbf{\sigma }={\mathbf{D}}_{\mathbf{e}}\cdot (\mathbf{d}\mathbf{\epsilon }-\mathbf{d}{\mathbf{\epsilon }}^{\mathbf{p}})=\left\{{\mathbf{D}}_{\mathbf{e}}-\frac{{\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T\otimes \frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}}{h+\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T}\right\}\cdot \mathbf{d}\mathbf{\epsilon }$$
$$\mathbf{d}\mathbf{\sigma }={\mathbf{D}}_{\mathbf{e}\mathbf{q}}\cdot \mathbf{d}\mathbf{\epsilon }\text{\hspace{1em}(11)}$$
$${\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T=\frac{3G}{2{\sigma }_{Mises}}\left[\begin{array}{cccccc}2G+\lambda & \lambda & \lambda & 0& 0& 0\\ \lambda & 2G+\lambda & \lambda & 0& 0& 0\\ \lambda & \lambda & 2G+\lambda & 0& 0& 0\\ 0& 0& 0& G& 0& 0\\ 0& 0& 0& 0& G& 0\\ 0& 0& 0& 0& 0& G\end{array}\right]\cdot \left\{\begin{array}{c}{\sigma }_{11}^{\prime }\\ {\sigma }_{22}^{\prime }\\ {\sigma }_{33}^{\prime }\\ 2{\sigma }_{12}^{\prime }\\ 2{\sigma }_{23}^{\prime }\\ 2{\sigma }_{13}^{\prime }\end{array}\right\}=\frac{3G}{{\sigma }_{Mises}}\left\{\begin{array}{c}{\sigma }_{11}^{\prime }\\ {\sigma }_{22}^{\prime }\\ {\sigma }_{33}^{\prime }\\ {\sigma }_{12}^{\prime }\\ {\sigma }_{23}^{\prime }\\ {\sigma }_{13}^{\prime }\end{array}\right\}$$
$$\begin{gathered} \left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T=\frac{9G^2}{{\sigma }_{Mises}^2}\left\{{\sigma }_{11}^{\prime },{\sigma }_{22}^{\prime },{\sigma }_{33}^{\prime },2{\sigma }_{12}^{\prime },2{\sigma }_{23}^{\prime },2{\sigma }_{13}^{\prime }\right\}\left\{\begin{array}{c}{\sigma }_{11}^{\prime }\\ {\sigma }_{22}^{\prime }\\ {\sigma }_{33}^{\prime }\\ {\sigma }_{12}^{\prime }\\ {\sigma }_{23}^{\prime }\\ {\sigma }_{13}^{\prime }\end{array}\right\} \\ =\frac{9G}{2{\sigma }_{Mises}^2}\frac{2}{3}\left[\frac{3}{2}\left({{\sigma }_{11}^{\prime }}^2+{{\sigma }_{22}^{\prime }}^2+{{\sigma }_{33}^{\prime }}^2+2{{\sigma }_{12}^{\prime }}^2+2{{\sigma }_{23}^{\prime }}^2+2{{\sigma }_{13}^{\prime }}^2\right)\right]=3G \end{gathered}$$
因此：
$$\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T=3G\text{\hspace{1em}(12)}$$
$$\begin{array}{l}{\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T\otimes \frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}=\\ \\ \frac{9}{4{\sigma }_{Mises}^2}\left\{\begin{array}{cccccc}{\sigma }_{11}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{22}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{33}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{12}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{23}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{13}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{13}^{\prime }\end{array}\right\}\end{array}\text{\hspace{1em}(13)}$$
(12)(13)代入(11):
$${\mathbf{D}}_{\mathbf{e}\mathbf{q}}=\left\{{\mathbf{D}}_{\mathbf{e}}-\frac{{\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T\otimes \frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}}{h+\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T}\right\}$$
$$\begin{array}{l}\frac{{\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T\otimes \frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}}{h+\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\cdot {\mathbf{D}}_{\mathbf{e}}\cdot {\left[\frac{\partial {\sigma }_{Mises}}{\partial \mathbf{\sigma }}\right]}^T}=\frac{9}{4{\sigma }_{Mises}^2(h+3G)}\\ \\ \left[\begin{array}{cccccc}{\sigma }_{11}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{22}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{33}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{12}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{23}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ {\sigma }_{13}^{\prime }\cdot {\sigma }_{11}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{22}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{13}^{\prime }\end{array}\right]\cdot \left[\begin{array}{cccccc}2G+\lambda & \lambda & \lambda & 0& 0& 0\\ \lambda & 2G+\lambda & \lambda & 0& 0& 0\\ \lambda & \lambda & 2G+\lambda & 0& 0& 0\\ 0& 0& 0& G& 0& 0\\ 0& 0& 0& 0& G& 0\\ 0& 0& 0& 0& 0& G\end{array}\right]\\ \\ =\frac{9G}{4{\sigma }_{Mises}^2(h+3G)}\left[\begin{array}{cccccc}2{\sigma }_{11}^{\prime }\cdot {\sigma }_{11}^{\prime }& 2{\sigma }_{11}^{\prime }\cdot {\sigma }_{22}^{\prime }& 2{\sigma }_{11}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{11}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ 2{\sigma }_{22}^{\prime }\cdot {\sigma }_{11}^{\prime }& 2{\sigma }_{22}^{\prime }\cdot {\sigma }_{22}^{\prime }& 2{\sigma }_{22}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{22}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ 2{\sigma }_{33}^{\prime }\cdot {\sigma }_{11}^{\prime }& 2{\sigma }_{33}^{\prime }\cdot {\sigma }_{22}^{\prime }& 2{\sigma }_{33}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{33}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ 2{\sigma }_{12}^{\prime }\cdot {\sigma }_{11}^{\prime }& 2{\sigma }_{12}^{\prime }\cdot {\sigma }_{22}^{\prime }& 2{\sigma }_{12}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{12}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ 2{\sigma }_{23}^{\prime }\cdot {\sigma }_{11}^{\prime }& 2{\sigma }_{23}^{\prime }\cdot {\sigma }_{22}^{\prime }& 2{\sigma }_{23}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{23}^{\prime }\cdot {\sigma }_{13}^{\prime }\\ 2{\sigma }_{13}^{\prime }\cdot {\sigma }_{11}^{\prime }& 2{\sigma }_{13}^{\prime }\cdot {\sigma }_{22}^{\prime }& 2{\sigma }_{13}^{\prime }\cdot {\sigma }_{33}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{12}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{23}^{\prime }& {\sigma }_{13}^{\prime }\cdot {\sigma }_{13}^{\prime }\end{array}\right]\end{array}$$
屈服后的DDSDDE(NTENS,NTENS)
$$DDSDDE(NTENS,NTENS)={\mathbf{D}}_{\mathbf{e}\mathbf{q}}$$

umat子程序

      SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
     1 RPL,DDSDDT,DRPLDE,DRPLDT,
     2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
     3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
     4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
C
      INCLUDE 'ABA_PARAM.INC'
C
      CHARACTER*80 CMNAME
      DIMENSION STRESS(NTENS),STATEV(NSTATV),
     1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
     2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
     3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
     4 JSTEP(4),
     5 STRESS_TR(NTENS),DSTRAN_P(NTENS),DSTRAN_E(NTENS),STRESS_D(NTENS),
     6 S_S(NTENS,NTENS)

      EE=PROPS(1)  !modulus
      EMU=PROPS(2)   !Possion's ritio
      EH=PROPS(3