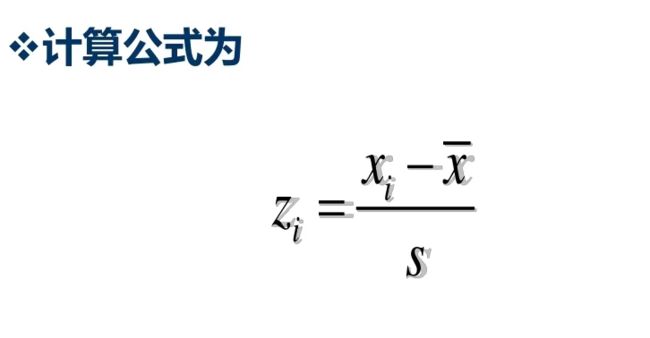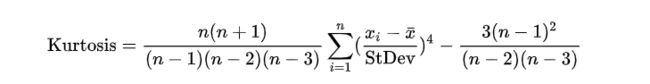统计学学习笔记三
4.2离散程度的度量
分类数据:异众比率
顺序数据:四分位差
数值型数据:方差和标准差
相对离散程度:离散系数
描述样本数据离散程度的统计量主要有全距、四分位距、方差、标准差以及测度相对离散程度的离散系数等
4.2.1全距和四分位距
1.全距
全距是一组数据的最大值与最小值之差,也称极差,用R表示。
R = max(x) - min(x)
容易受极端值的影响,不能全面反映数据的差异状况。虽然全距在实际中很少单独使用,但是它总是作为分析数据离散程度的一个参考值
2.四分位距
一组数据75%位置上的四分位数与25%位置上的四分位数之差,也称四分位差,用IQR表示
IQR = Q75% - Q25%
四分位距反映了中间50%数据的离散程度:其数值越小,说明中间的数据越集中,数值越大,说明中间的数据越分散。四分位距不受极值的影响。
由于中位数处于数据的中间位置,因此,四分位距的大小在一定程度上也说明了中位数对一组数据的代表程度
4.2.2方差和标准差
数据离散程度的最常用测度值
反映了各变量值与均值的平均差异
标准差为方差的开方
根据总体数据计算的,称为总体方差(标准差),记为(σ);根据样本数据计算的,称为样本方差(标准差),记为 (s)
平均差,也称平均绝对离差:将离差取绝对值,求和再平均得出的结果
方差:将离差平方后再求平均数得到的结果
标准差:方差开方后的结果
方差(或者标准差)是实际中应用最广泛的测度数据离散程度的统计量
4.2.3离散系数
标准差是反映数据离散程度的绝对值,11其数值的大小受原始数据取值大小的影响,数据的观测值越大,标准差的值通常也就越大
标准差与原始数据的计量单位相同,采用不同计量单位计算的数据,其标准差的值也就不同
对于不同组别的数据,如果原始数据的观测值相差较大或者计量单位不同,就不能用标准差直接比较,这是需要计算离散系数
离散系数(CV):
又称变异系数,是统计学当中的常用统计指标。离散系数是测度数据离散程度的相对统计 量,主要是用于比较不同样本数据的离散程度。离散系数大,说明数据的离散程度也大;离散系数小,说明数据的离散程度也小。
一组数据的标准差与其相应的平均数之比。离散系数消除了数据取值大小和计量单位对标准差的影响,因此可以反映一组数据的相对离散程度
CV = s / 平均数x(标准差与平均数的比值(相对值)
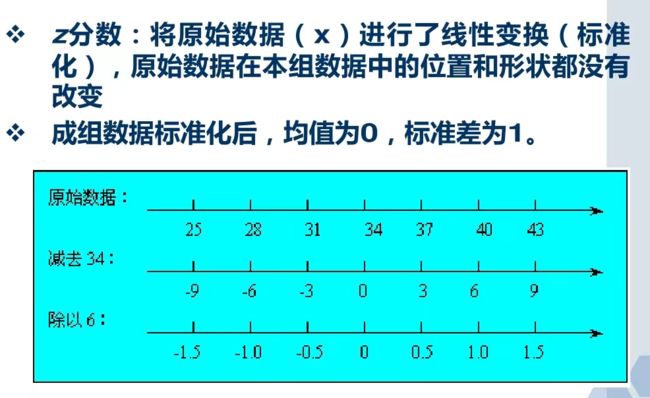
4.2.4标准分数
也叫z分数,是一种具有相等单位的量数。它是将原始分数与团体的平均数之差除以标准差所得的商数,是以标准差为单位度量原始分数离开其平均数的分数之上多少个标准差,或是在平均数之下多少个标准差。它是一个抽象值,不受原始测量单位的影响,并可接受进一步的统计处理。
有了平均数和标准差之后,可以计算一组数据中每个数值的标准分数。它是某个数据与其平均数的离差除以标准差后的值。
标准分数可以测度每个数值在该组数据中的相对位置,并可以用来判断一组数据是否有离群点。
例:全班平均考试分数为80分,标准差为10分,你的考试分数是90分,与平均分有1个标准差的距离
这里的1就是你考试成绩的标准分数
标准分数说的是某个数据与平均数相比相差多少个标准差
将一组数据化为标准化得分的过程称为数据的标准化
在对多个具有不同量纲的变量进行处理时,常常需要对各变量的数据进行标准化处理,也就是把一组数据转化为具有平均数为0、标准差为1的新数据。
标准分数只是将原始数据进行了线性变换,它没有改变某个数值在该组数据中的位置,也没有改变该组数据分布的形状
判断一组数据中是否存在离群点
对称分布的数据(经验法则):
当一组数据对称分布时,约有68%的数据在平均数加减1个标准差的范围之内;
约有95%的数据在平均数加减2个标准差的范围之内;
约有99%的数据在平均数加减3个标准差的范围之内
在平均数加减3个标准差的范围之内几乎包含了全部数据,而在3个标准差之外的数据在统计上也称为离群点。
适合任何分布形态的数据(切比雪夫不等式):
切比雪夫不等式提供的是“下界”,也就是“所占比例至少是多少”
对于任意分布形态的数据,根据切比雪夫不等式,至少有(1-1/k的平方)的数据落在+-k个标准差之内。其中k是大于1的任意值,但不一定是整数。
对于k= 2,3,4,该不等式的含义是:
至少有75%的数据在平均数+-2个标准差的范围之内
至少有89%的数据在平均数+-3个标准差的范围之内
至少有94%的数据在平均数+-4个标准差的范围之内
4.3分布形状的度量
偏度系数和峰值高低的一种度量
4.3.1偏度系数
偏度是指数据分布的不对称性,测度数据分布不对称性的统计量称为偏度系数,记为SK
当分布左右对称时,偏度系数为0。当偏度系数大于0时,即重尾在右侧时,该分布为右偏。当偏度系数小于0时,即重尾在左侧时,该分布左偏。
若偏度系数大于1或者小于-1,视为严重偏斜分布;若偏度系数在0.5~1或者-1~-0.5之间时,视为中等偏斜分布;若偏度系数在0~0.5或者-0.5~-0之间时,视为轻微偏斜。其中负值表示左偏分布(在分布的左侧有长尾),正值则表示右偏分布(在分布的右边有长尾)
4.3.2峰度系数
峰度:数据分布峰值的高低
测度一组数据分布峰值高低的统计量称为峰度系数,记作K
表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量,如果峰度大于三,峰的形状比较尖,比正态分布峰要陡峭。反之亦然。
在统计学中,峰度(Kurtosis)衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。
峰度通常是与标准正态分布相比较而言的。由于标准正态分布的峰度系数为0,当K>0时为尖峰分布,数据分布的峰值比标准正态分布高,数据相对集中;当K<0时为扁平分布,数据分布的峰值比标准正态分布低,数据相对分散。