蓝桥杯 试题 算法训练 印章 C++ 详解
题目:
共有n种图案的印章,每种图案的出现概率相同。小A买了m张印章,求小A集齐n种印章的概率。
前言:
建议先看以下两篇文章:(我也是看了之后才懂得)
https://blog.csdn.net/okok__TXF/article/details/121099645
https://blog.csdn.net/m0_58245389/article/details/121877031
然后是我个人做题时有遇到一些问题,所以打算自己尝试再详细解释一下过程。
因为一开始我想的是:
用二维数组的每一个元素的值表示答案(概率),对应的下标(i,j)为印章种类n,印章张数m。然后我就一直找概率和 i , j 的关系,企图用数学公式求出所有的答案,再以n,m为下标去数组中取出答案……然后就解不出这道题,最多50%的准确率。(n > m, n == m)
然后看网上的解题思路才知道自己太死板了。网上用二维数组是为了求出最终的结果,二维数组中其余的数值都只是为了求出答案做铺垫而已。
但是因为自己一开始思维定势是认为网上也是二维数组,跟自己的想法应该是一样的,只是数学公式问题而已,这样去看题导致我迷迷糊糊,看不懂网上的解题过程,造成不小的困扰……
所以想详细解释一下网上的解题过程,希望有和我一样,或者看了上面两篇文章也还是迷迷糊糊的同学看了我的解释之后能对这道题的解题思路更加清晰。
开始:(前提是各位同学看过前面两篇文章,对这道题已经有一定的了解)
首先我们已经知道了印章的种数n,和印章的张数m。
然后我们用二维数组的行下标 i ,列下标 j ,分别比作印章的种数n,和印章的张数m。
( double dd[21][21]; double P = 1.0 / n; int n, m; )
这句话很重要:dd[i][j] 表示买了 j 张,凑齐 i 种的概率。
同时记得:n,m和i,j是不太一样的概念,可认为:n,m是最终结果的下标,i,j是过程结果的下标。
(确实有点绕,但后面看着看着应该就理解了)
接下来分情况讨论:
一、n > m (i > j)。明显 dd[i][j] = 0;
如果印章的种数大于购买印章的张数,那么是不可能集齐所有种数的印章的。概率即为:0
二、n <= m 。
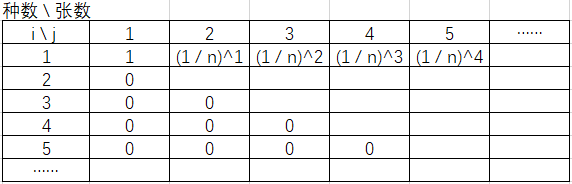
1. i == 1 【表示凑齐 1 种印章。只认为集齐 1 种印章,不论张数】
当 j == 1 时,dd[i][j] =1.0 = P * n; 买 1 张,凑齐 1 种印章的概率
当 j == 2 时,dd[i][j] = P = P * P * n; 买 2 张,凑齐 1 种印章的概率
当 j == 3 时,dd[i][j] = P * P = P * P * P * n; 买 3 张,凑齐 1 种印章的概率
……
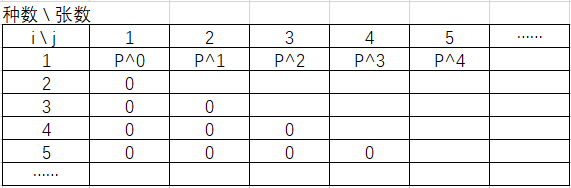
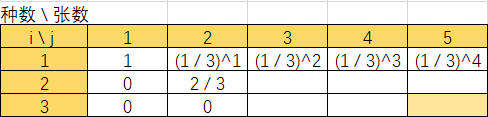
即当 i == 1 时,dd[i][j] = dd[1][j] = P ^ (j - 1);
对照这个表理解:
2. i >= 2 【表示凑齐 2(3,4,5,……,n)种印章】
首先是 i == 2, j == 2 。此时,dd[2][2] = dd[i][j] 所表示的含义:买 2 张凑齐 2 种的概率。
那么可以分为两种情况讨论:
<1>前 j - 1 张已经凑齐了 i 种。(当然这种情况这里没有,下一个再举例)
<2>前 j - 1 张已经凑齐了 i - 1 种。所以第 j 张只需要凑齐 i 种,即:买到前面没有出现过的种类。
dd[i - 1][j - 1] * (n - (i - 1)) / n ,即 之前的概率 乘 (买到剩余种类商品的概率)
所以 dd[i][j] = 0 + dd[i - 1][j - 1] * (n - (j - 1)) / n
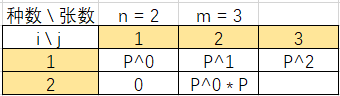
举例:n = 2, m = 2; 则P = 1.0 / 2。dd[n][m] = dd[2][2] = dd[1][1] * (2-(2-1))/n = P^0 * P = 1 / 2
(还是不太理解也没关系的,接着往下看)
然后是 i == 2, j == 3 。此时
分情况讨论:
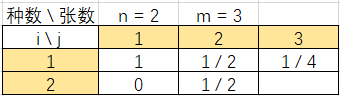
举例:n = 2, m = 3; 则P = 1.0 / 2。
<1>前 j - 1 张已经凑齐了 i 种。(上面缺失的情况,这里补充)
现在是不是前面 dd[2][2] = dd[i][j - 1] 就已经集齐,前 2 张就已经凑齐了 2 种。那么接下来是不是只需要再买到之前已经买过的种类就行。即:dd[2][2] * i / n
注意:可能有人会对这里有所疑惑,既然已经凑齐,那还要再去买之前买过的种类呢?其实这个公式是为后面的计算提供的,(但其实代入也是*1而已)也是我这里没有举例好的缘故。就比如说:n = 10, m = 10. 但是 i = 2, j = 3这里的概率同样是这样计算的。还是前面所说的n,m是和i,j相区分的。不论n和m,dd[2][3]仅仅讨论买3张凑齐2种的概率。
<2>前 j - 1 张已经凑齐了 i - 1 种。所以第 j 张只需要凑齐 i 种,即:买到前面没有出现过的种类。
dd[i - 1][j - 1] * (n - (i - 1)) / n ,即 之前的概率 乘 (买到剩余种类商品的概率)
同上:dd[2][3] = dd[2][2] * 2 / 2 + dd[1][2] * (2 - (2 - 1)) / 2 = 1 / 2 + 1 / 2 * 1 / 2 = 3 / 4 = 0.75
总之,求dd[i][j],利用dd[i][j - 1]和dd[i - 1][j - 1]可求。
最后得到的公式是:dd[i][j] = dd[i][j - 1] * i / n + dd[i - 1][j - 1] * (n - (i - 1)) / n;
解释:买 j 张集齐 i 种的概率 =
买 j-1 张集齐 i 种的概率 * 第 j 张买到前面买过的 i 种的概率 +
买 j-1 张集齐 i-1 种的概率 * 第 j 张买到前面没有买过的 i - 1 种的概率
接下来我们再举一个例子:
n = 3, m = 5; 可知:P = 1.0 / 3
01、i = 2, j = 2 买2张,凑齐2种的概率。
<1>前1张就凑齐了2种:dd[1][2] = 0;<2>前1张凑齐了1种:dd[1][1] = 1;
所以:dd[2][2] = 0 * 2 / 3 + 1 * (3 - 1) / 3 = 2 / 3
在前1张凑齐2种的概率 * 在第2张的时候买到之前买到的种类中的任一一种的概率
总的种类:3,已经买过的种类:2,所以:2 / 3;
在前1张凑齐1种的概率 * 在第2张的时候买到之前没有买到的种类的概率
总的种类:3,没有买过的种类:3 - 1,所以:(3 - 1) / 3;
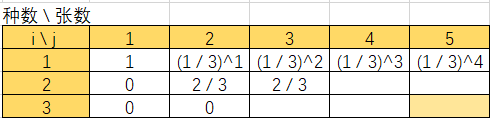
02、i = 2, j = 3 买3张,凑齐2种的概率。
<1>前2张就凑齐了2种:dd[2][2] = 2 / 3;<2>前2张凑齐了1种:dd[1][2] = 1 / 3;
所以:dd[2][3] = (2 / 3) * (2 / 3) + (1 / 3) * (3 - 1) / 3 = 2 / 3
在前2张凑齐2种的概率 * 在第2张的时候买到之前买到的种类中的任一一种的概率
总的种类:3,已经买过的种类:2,所以:2 / 3;
在前2张凑齐1种的概率 * 在第2张的时候买到之前没有买到的种类的概率
总的种类:3,没有买过的种类:3 - 1,所以:(3 - 1) / 3;
03、……
以此类推,我就偷一下懒,方便各位同学思考。
总结:(本来是想着把网上的答案简单详细的解释一下,结果感觉更加复杂了……但还是希望各位同学能理解,我也是初学者)如果有较好的编程思维,这道题还是不难的。但像我,一开始思路就错了,后面理解起来就比较麻烦。
最后附上代码:
#include
using namespace std;
#include
int main()
{
int n, m;
cin >> n >> m;
double dd[21][21] = { 0.0 };
double P = 1.0 / n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (i == 1)
{
dd[i][j] = 1.0;
for (int k = 1; k < j; k++)
{
dd[i][j] *= P;
}
}
else
{
dd[i][j] = dd[i][j - 1] * (i * P) + dd[i - 1][j - 1] * ((n - (i - 1)) * P);
}
}
}
cout << fixed << setprecision(4);
//for (int i = 1; i <= n; i++)
//{
// for (int j = 1; j <= m; j++)
// {
// cout << dd[i][j] << "\t";
// }
// cout << endl;
//}
cout << dd[n][m];
return 0;
} 希望各位同学能理解。