【状态估计】用于描述符 LTI 和 LPV 系统的分析、状态估计和故障检测的算法（Matlab代码实现）

欢迎来到本博客 ❤️ ❤️


博主优势： 博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。


⛳ 座右铭：行百里者，半于九十。

本文目录如下：
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码、数据、文章讲解

1 概述

文献来源：

摘要:本文讨论了在LTI或LPV描述子框架中建模的系统的MATLAB/SCILAB工具箱的开发。给出了正则性、可解性、可控性和可观测性。包括全阶观测器和降阶观测器，比例观测器和比例积分观测器。其中一些观察人士考虑了未知的输入。可以作为基于状态估计和故障检测的观测器的辅助工具。这些观察者已经从最近发表的几篇论文中得到了考虑。通过建立观测库来实现故障的检测和隔离。这些观察者库可以通过选择输入/输出矩阵来建立，也可以使用所提出的算法自动建立。

许多系统都可以用非线性微分方程来建模，但是监控系统的设计是一项困难的任务。因此，对非线性系统进行线性化以获得线性时不变(LTI)系统是非常常见的，但这种表示在一个平衡点或工作点附近是有效的。

改进模型表示的一种方法是包含一些限制。如果限制是模型的一部分，那么系统就变成了描述符- lti (DLTI)表示。DLTI系统的主要优点是集成了静态关系(例如物理约束)和动态关系。这些考虑允许对广泛的过程进行建模，例如，在Dai, 1989;段,2010)。

Luenberger观测者存在的充分条件在(Hou and Muller, 1999;Darouach和Boutayeb, 1995)。(Darouach等人，1996)的作者提出了一种降阶未知输入观测，类似于(Chen和Patton, 1999)中研究的LTI系统的观测器。

详细文章讲解及数学模型见第4部分。

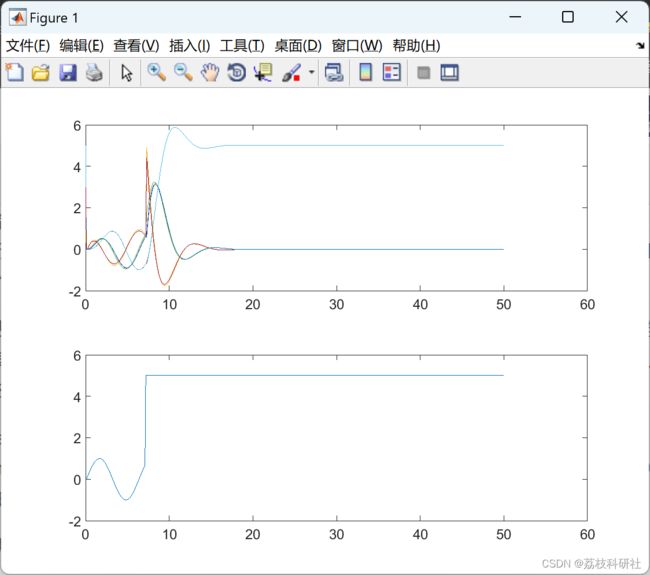
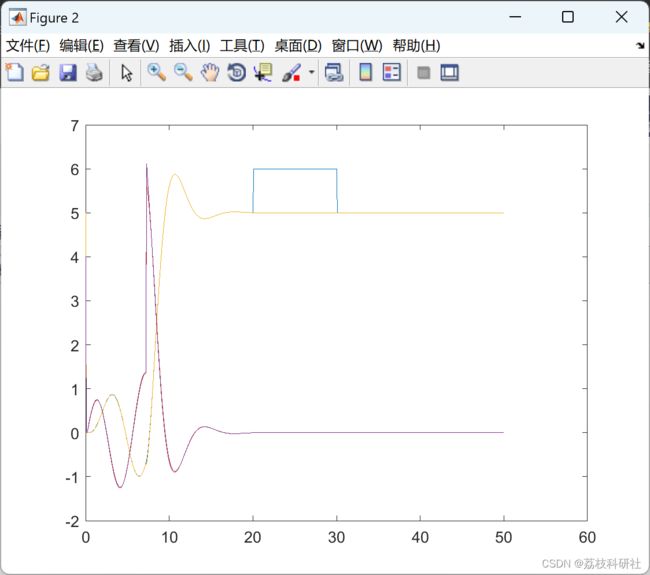
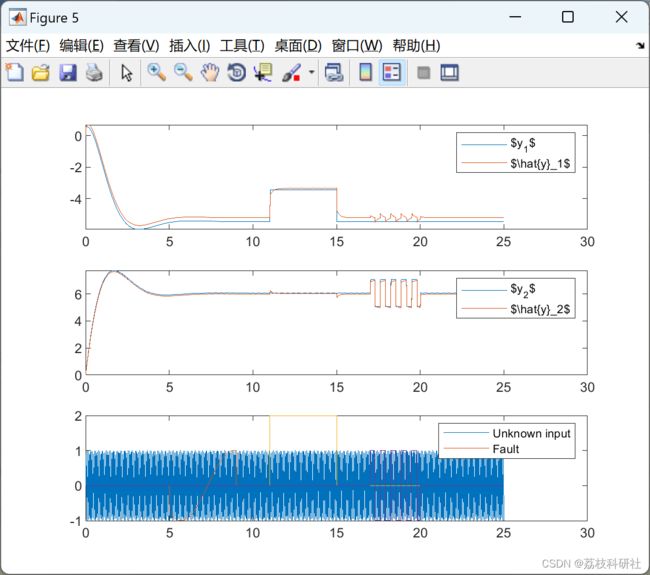
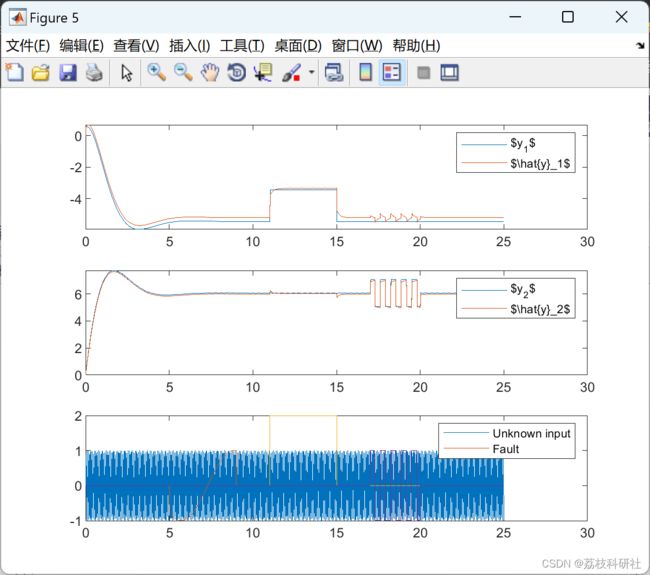
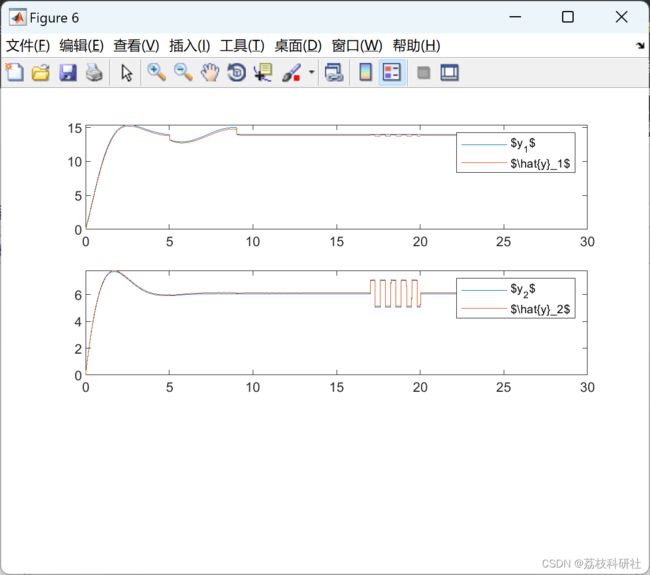
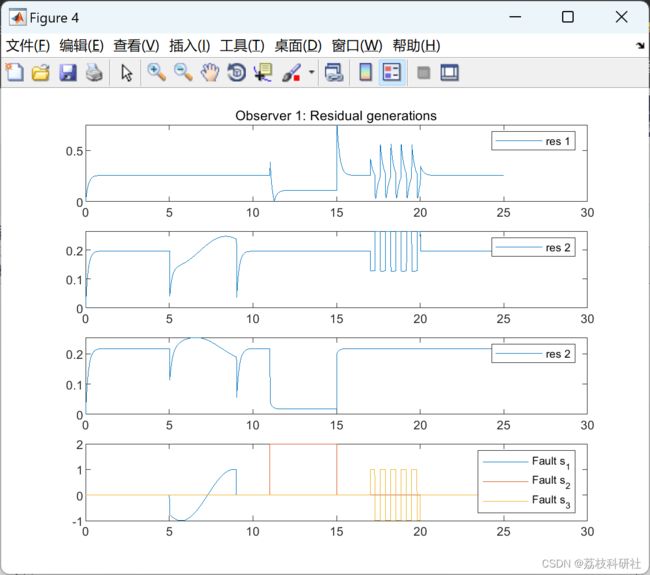
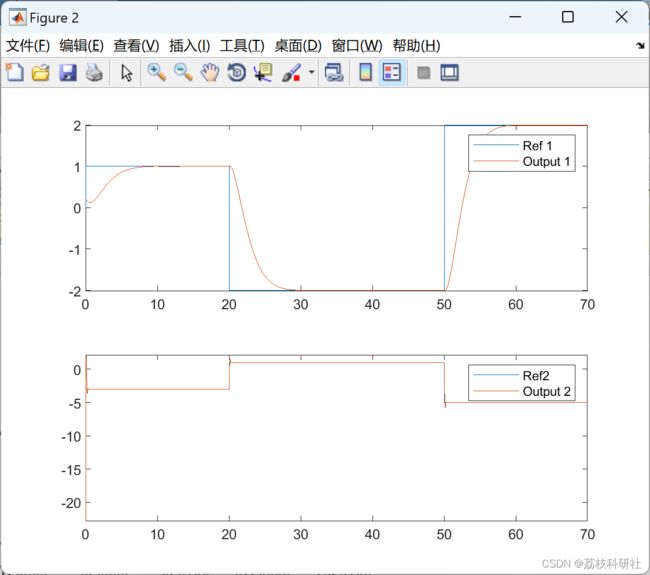
2 运行结果

部分代码：

xe=[ 1 5 3 0]'% intial stimated states

ye(:,1)=C*xe % compute the initial output

t(1)=0;% initial time

u(1)=0;

% observer gains

% % if the system is observable then compute the restricted system equivalence systems by QR descomposition

disp('Simulation')

for k=1:50/Te

% Time counter

t(k+1)=t(k)+Te;

% input

if t(k)<7

u(k+1)=1;

else

u(k+1)=5;

end

% % the differentials equations can be solved by runge-kuta of four order

x1=x1+Te*(x3);

x2=x2+Te*(x1);

x4=x1;

x3=-x2-x4+u(k);

xx(:,k+1)=[x1 x2 x3 x4]';

y(:,k+1)=C*xx(:,k+1); % system output

% Observer

yi=[-Be1*u(k);y(:,k)]; % auxiliar for compute the observer

% Reduced order observer

% $z=Piz+Lyi+H*u $

% $\hat{x}=Mz+Fyi$

z(k+1)=z(k)+Te*(Pi*z(k)+L*yi+H*u(k)); %

xe(:,k+1)=M*z(k)+F*yi;

ye(:,k+1)=C*xe(:,k+1); % stimated output

% Generation of residuos

end

disp('PLOTS')

pause

figure(2);

cla();

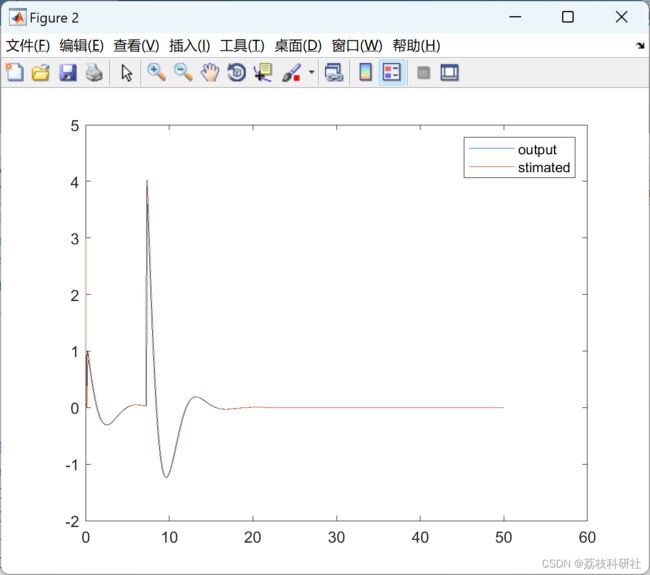
plot(t,y',t,ye')

legend('output', 'stimated')

n=size(A,1);

m=size(B1,2);

p=size(C,1);

if flag==1

P=sdpvar(n,n);

Y=sdpvar(m,n,'full');

Q=sdpvar(1,n,'full');

sdpvar g

% g=0.1

alpha=0;

Con=[P>=0,g>=0];

LMI=blkvar();

LMI(1,1)= (P*E'+S*Q)'*A'+Y'*B1'+A*(P*E'+S*Q)+B1*Y+B*B'+2*alpha*P;

LMI(1,2)=E*P'*C'+Q'*S'*C'+Y'*B2';

% (P*E'+S*Q)'*C'+Y'*B2';

LMI(2,2)=-g*eye(p);

LMI=sdpvar(LMI);

Con=[Con, LMI<=0]

op=sdpsettings('verbose',0,'solver','sedumi','sedumi.eps',1e-5);

solvesdp(Con,[],op)

P=double(P);

Y=double(Y);

Q=double(Q);

g=double(g);

% K=Y/((P*E'+S*Q))

K=Y/((P*E'+S*Q))

lamda=deig(A+B1*K,E)

% [Ccon, Rcon, Icon]=dcontr (E,A+B*K,B)

elseif flag==2

% g=0.01100

cvx_begin sdp

cvx_precision default

cvx_solver sedumi

variable g

variable P(n,n) symmetric

variable Y(m,n)

variable Q(1,n)

minimize g

P >= 0

[ (P*E'+S*Q)'*A'+Y'*B1'+A*(P*E'+S*Q)+B1*Y+B*B' E*P'*C'+Q'*S'*C'+Y'*B2' ; ...

(E*P'*C'+Q'*S'*C'+Y'*B2')' -g*eye(p)] <= 0

cvx_end

gamma = sqrt(g)

K=Y/((P*E'+S*Q));

lamda=deig(A+B1*K,E)

else

setlmis([]);

% create a blank LTI framework

P=lmivar(1,[n 1]); % declare X as a 3 脳 3 symmetrical matrix

Y=lmivar(2,[m n]); % declare Y as a n x n

Q=lmivar(2,[1 n]); % declare

lmiterm([1 1 1 P],A,E','s') % A*P*E' + *

lmiterm([1 1 1 Q],A*S,1,'s') % A*S*Q+*

lmiterm([1 1 1 Y],B1,1,'s') % B*Y+*

lmiterm([1 1 1 0],B*B') % B*B'+*

lmiterm([1 1 2 P'],E,C') % E*P'*C'

lmiterm([1 1 2 Q'],1,S'*C') % Q'*S'*C'

lmiterm([1 1 2 Y'],1,B2') % E*P'*C'

% lmiterm([1 1 1 P],2*5,1,'s') % B*Y+*

lmiterm([-2 1 1 P],1,1,'s') % P>0

% lmiterm([-3 1 1 Q],1,1) % P>0

Con=getlmis;

% c = mat2dec(Con,eye(3),eye(3),eye(1,n));

% options = [1e5,0,0,0,0];

% [copt,b] = mincx(Con,c,options);

[tmin b]=feasp(Con);

% [tmin b]=mincx(Con,-trac);

P=dec2mat(Con,b,P);

Y=dec2mat(Con,b,Y);

Q=dec2mat(Con,b,Q);

K=Y/((P*E'+S*Q));

lamda=deig(A+B*K,E);

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

4 Matlab代码、数据、文章讲解