时间序列分析卫星重力梯度观测值
阚昊宇
1 时间序列图
导入数据,共2880历元(86370 s)数据,取前2400历元(72000
s)数据作为训练集,后480历元作为测试集。将训练集绘制时间序列图如下图
1红色线所示,可见明显的自相关性及线性、余弦周期项趋势。
图 1 Vzz时间序列
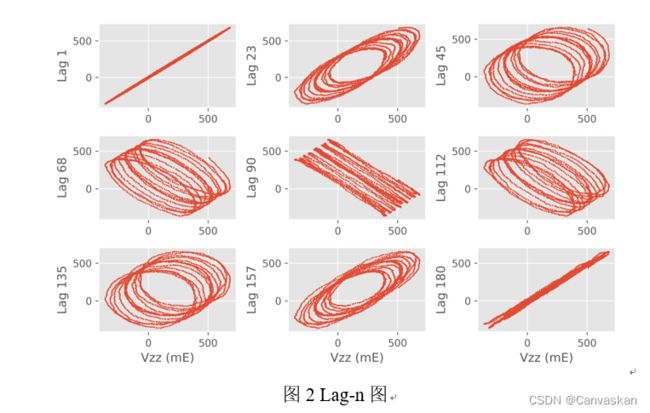
绘制不同lag(n=1,23,45,68,90,112,135,157,180)如下图
2所示,进一步验证了强烈的自相关性及余弦周期项趋势。
图 2 Lag-n图
2 拟合并扣除线性趋势
对训练集数据进行线性趋势拟合,得到拟合结果和扣除线性趋势的Vzz时间序列如下图
3所示,其中,蓝色虚线为线性拟合结果。线性趋势拟合包括截距项,因此去除线性趋势后的Vzz序列平均值为0。
图 3 线性趋势拟合与去除
线性拟合采用ordinary least squares (OLS)方法进行,拟合报告细节部分如下表
1所示。
表 1 线性拟合回归报告
3 拟合并扣除余弦趋势
去除线性趋势后,仍有显著余弦趋势项,进行余弦趋势拟合,结果如下图
4所示,其中蓝色虚线为余弦拟合结果,下半图红色线为去除余弦趋势的残差序列。
图 4 余弦趋势拟合与去除
4 两轮拟合后残差的QQ图、直方图
经过线性拟合和余弦趋势项拟合的残差序列直观感受并不接近白噪声序列,对其进行QQ图、直方图和t分布拟合分析如下图
5、图 6所示。由图
5,残差分布在QQ图上并不贴合45°角直线,而成S形,说明残差并不符合正态分布。由图
6,残差概率分布直方图也与相应的t分布(经过平移和缩放处理)不符合。因此,判断残差不满足正态性。
图 5 残差QQ图 图 6 残差概率分布直方图与t分布拟合
5 ARMA定阶
即使残差时间序列不满足正态性,由于残差序列可以视为平稳的,仍然可以采用ARMA(p,q)模型对于来自第3节中的残差时间序列进行建模,其自相关函数和偏自相关函数图如下图
7、图 8所示。
自相关图(ACF)显示拖尾;偏自相关图(PACF)显示3阶截尾,因此由ACF、PACF得到的最优ARMA模型阶数应当为(3,0)。
图 7 自相关图 图 8 偏自相关图
6 ARMA模型预报结果
将数据前2400历元作为训练集,后480历元作为测试集,经过第2、3节的预处理操作提取线性、余弦趋势项后,将残差采用ARMA(3,0)模型进行拟合及预报。得到残差拟合及预报结果如下图
9,其中黑色线为真值,蓝色实线为ARMA模型拟合结果,蓝色虚线为ARMA模型预报结果,蓝色半透明区域为预报95%置信区间。可见,ARMA(3,0)模型拟合效果很好,拟合结果基本与训练集数据重合;短时间(约3600
s)对于残差预测效果较好,长时间预测则仅能预测残差数据趋势,在残差变化量级上相差甚远。
图 9 残差ARIMA(3,0,0)拟合及预报结果
图 10 原始数据ARIMA(3,0,0)拟合及预报结果
采用训练集拟合得到的线性、余弦趋势,扩展到测试时间段,并叠加预测得到的残差序列,得到预报结果如图
10所示,可见,该线性+余弦+ARIMA残差预报可以在一定程度上对Vzz时间序列进行预报,真值结果基本落入预报的95%置信区间。
7 其他阶数ARIMA模型预报效果对比
采用p={0,1,2,3},d={0,1,2},q={0,1,2,3}的所有组合,进行不同阶数的ARIMA(p,d,q)模型建模及预报,所得到的AICC(Akaike
information criterion corrected)及训练集拟合精度(FIT_RMS)、测试集预报精度(TEST_RMS)如表2所示,其中,最小值标红。可见,AICC指标和模型拟合精度FIT_RMS最小的模型为ARIMA(2,1,3),其模型拟合精度也较高,但是其模型测试精度(60.7)远低于通过ACF、PACF图定阶得到的ARIMA(3,0,0)模型,说明ACF、PACF图示法定阶在此次建模过程中具有较高有效性。
表 2 不同阶数ARIMA(p,d,q)模型AICC及拟合、测试精度(最小值标红)
p d q AICC FIT_RMS TEST_RMS
0 0 0 20942.12 18.98 41.37
0 0 1 18196.91 10.72 41.37
0 0 2 16454.06 7.46 41.37
0 0 3 15378.94 5.97 41.37
0 1 0 12218.68 3.12 61.43
0 1 1 12152.95 3.08 60.79
0 1 2 12151.54 3.08 60.55
0 1 3 12153.50 3.08 60.53
1 0 0 12216.46 3.14 43.17
1 0 1 12155.93 3.09 44.97
1 0 2 12155.42 3.10 43.55
1 0 3 12157.43 3.10 43.57
1 1 0 12159.74 3.09 61.00
1 1 1 12151.52 3.08 60.5
1 1 2 12153.49 3.08 60.52
1 1 3 12155.56 3.08 60.55
2 0 0 12161.87 3.11 42.85
2 0 1 12155.35 3.09 45.4
2 0 2 12157.45 3.10 43.45
2 0 3 12159.12 3.09 45.38
2 1 0 12152.70 3.08 60.71
2 1 1 12153.49 3.08 60.52
2 1 2 12155.50 3.08 60.52
2 1 3 12147.16 3.07 60.7
3 0 0 12156.12 3.10 43.32
3 0 1 12157.37 3.10 43.92
3 0 2 12159.29 3.09 45.39
3 0 3 12161.31 3.10 43.76
3 1 0 12153.78 3.08 60.60
3 1 1 12155.49 3.08 60.52
3 1 2 12157.51 3.08 60.52
3 1 3 12149.17 3.08 60.69
8 总结
本次作业中,对一份卫星重力梯度观测值Vzz分量(重力位二阶径向导数)时间序列进行了如下分析,并得出相关初步结论:
-
进行时间序列绘图,直观判断其具有明显的趋势项和周期项,后通过绘出Lag-n图确认其相关性及周期性;
-
通过线性趋势拟合、余弦趋势拟合得到Vzz残差;
-
通过残差QQ图、概率分布直方图和t分布拟合分析扣除线性趋势、余弦趋势的残差仍然不满足正态性;
-
由于残差序列近似平稳,因此仍可以采用ARMA模型进行建模;
-
对序列的ACF、PACF图进行分析,定阶得到ARMA(3,0)模型;测试得到ARMA(3,0)模型在短时间(约3600
s)对于残差预测效果较好,长时间则仅能粗略预测残差数据趋势; -
通过不同阶数ARIMA模型预报结果对比,发现对于本次作业中的Vzz样本,采用AICC及拟合精度定阶方法得到的ARIMA模型,在测试集的表现上不如ACF、PACF图直观定阶得到的模型精度,说明ACF、PACF图定阶方法具有有效性。
由于残差序列近似平稳,因此仍可以采用ARMA模型进行建模; -
对序列的ACF、PACF图进行分析,定阶得到ARMA(3,0)模型;测试得到ARMA(3,0)模型在短时间(约3600
s)对于残差预测效果较好,长时间则仅能粗略预测残差数据趋势; -
通过不同阶数ARIMA模型预报结果对比,发现对于本次作业中的Vzz样本,采用AICC及拟合精度定阶方法得到的ARIMA模型,在测试集的表现上不如ACF、PACF图直观定阶得到的模型精度,说明ACF、PACF图定阶方法具有有效性。