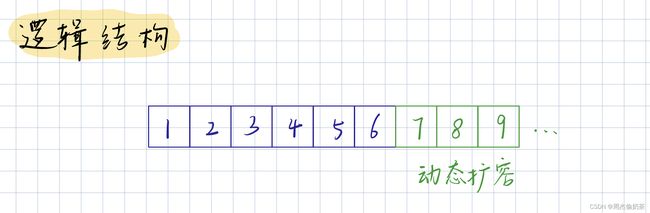【数据结构初阶-线性表】顺序表和链表,多图详解
前言
本期玩玩线性表中的 顺序表、单向链表、带头双向循环链表
1. 线性表
:一种数据结构的大类,有限序列,元素特性相同,逻辑结构连续
如,顺序表,链表,栈,队列…
顺序表在物理结构上也连续,链表在物理结构上不连续:
*物理结构: 内存中存储的结构
1.1 顺序表
:一种线性表,物理结构上连续
既然要求物理结构连续,那数组很适合用来实现顺序表
一般顺序表有两种:
- 静态顺序表:用定长数组实现(不常用,满了就没法用了)
- 动态顺序表:用动态开辟的数组实现
大多情况,都用动态顺序表…
逻辑结构如下:
1.1.1 实现&分析
类型声明
顺序表需要 数组arr、数量size、容量capacity 来实现,自然用结构体封装起来比较合适
typedef int SLDataType;//方便修改顺序表的数据类型
typedef struct SeqList
{
SLDataType* arr;//用指针可以动态开辟
int size;//记录数量
int capacity;//当前容量
}SL;//方便使用
- arr:保存顺序表内元素的值
- size:记录数量
- capacity:记录容量
讲接口之前,首先得了解一个重要原则:高内聚,低耦合。
^内聚:接口内部聚集的程度,一个好的内聚模块,应该恰好只完成它指定的任务
^耦合:表示两个接口之间的关联程度,当一个接口发生变化时对另一个接口的影响很小,则称低耦合;反之,如果变化的影响很大时,则称高耦合
解惑1:为什么要“高内聚低耦合”?
符合这个原则的代码,可重用性高、可移植性高
如果接口之间功能重复,互相影响……能运行出正常的程序就真是太幸运了
所以,我们接下来的实现都遵循 “高内聚,低耦合” 的原则
接口声明
void SLInit(SL* psl);
void SLDestroy(SL* psl);
void SLPrint(SL* psl);
void CheckCapacity(SL* psl);
void SLPushFront(SL* psl, SLDataType x);
void SLPopFront(SL* psl);
void SLPushBack(SL* psl,SLDataType x);
void SLPopBack(SL* psl);
int SLFind(SL* psl, SLDataType x);
void SLInsert(SL* psl, int pos, SLDataType x);
void SLErase(SL* psl, int pos);
接口测试
void test1()
{
SeqList sl;//创建顺序表结构体
SeqListInit(&sl);//初始化顺序表:arr,size,capacity
//头插
SeqListPushFront(&sl, 1);//需要修改顺序表结构体,传结构体指针
SeqListPushFront(&sl, 2);
SeqListPushFront(&sl, 3);
SeqListPushFront(&sl, 4);
SeqListPrint(&sl);
//头删
SeqListPopFront(&sl);//需要改变结构体,传结构体指针
SeqListPopFront(&sl);
SeqListPopFront(&sl);
SeqListPopFront(&sl);
SeqListPrint(&sl);
//尾插
SeqListPushBack(&sl, 10);
SeqListPushBack(&sl, 20);
SeqListPushBack(&sl, 30);
SeqListPushBack(&sl, 40);
SeqListPrint(&sl);
//尾删
SeqListPopBack(&sl);
SeqListPopBack(&sl);
SeqListPopBack(&sl);
SeqListPopBack(&sl);
SeqListPrint(&sl);
SeqListDestroy(&sl);
}
void test2()
{
SeqList sl;
SeqListInit(&sl);
SeqListPushBack(&sl, 11);
SeqListPushBack(&sl, 22);
SeqListPushBack(&sl, 33);
SeqListPushBack(&sl, 44);
SeqListPrint(&sl);
//查找
int pos = SeqListFind(&sl, 44);
//插入
SeqListInsert(&sl, pos, 999);
SeqListPrint(&sl);
//删除
SeqListErase(&sl, pos);
SeqListPrint(&sl);
SeqListDestroy(&sl);
}
int main()
{
test2();
return 0;
}
功能接口实现
初始化
思路:全部成员置空
void SLInit(SL* psl)
{
assert(psl);
psl->arr = NULL;
psl->capacity = psl->size = 0;
}
- psl为空没法访问对象
销毁
思路:释放顺序表结构内的数组,其他成员置空
void SLDestroy(SL* psl)
{
assert(psl);
free(psl->arr);
psl->arr = NULL;
psl->capacity = psl->size = 0;
}
- psl为空没法访问对象
打印
思路:遍历
void SLPrint(SL* psl)
{
assert(psl);
int i = 0;
for (i = 0; i < psl->size; i++)
{
printf("[%d] ", psl->arr[i]);
}
printf("\n");
}
检查容量
思路:如果表空,默认开辟2个元素的空间;如果表满,扩容2倍
void CheckCapacity(SL* psl)
{
assert(psl);
//size == capacity 代表顺序表满了
if (psl->size == psl->capacity)
{
//如果是第一次开辟空间,就给个默认值2,否则扩容2倍
int newcapacity = psl->capacity == 0 ? 2 : 2 * psl->capacity;
SLDataType* tmp = (SLDataType*)realloc(psl->arr, newcapacity * sizeof(SL));
if (tmp == NULL)
{
perror("realloc");
exit(-1);
}
psl->arr = tmp;
psl->capacity = newcapacity;
}
}
- realloc:拿到NULL的时候,执行的是malloc的功能,所以可以解决表空的情况
- 咱们实现的扩容是默认扩2倍,不容易开多,浪费空间;也不容易开少,频繁开辟
增删查改接口实现
关于移动数组元素,跟大家分享一个小技巧:
移动数组元素分两种情况:
- 往前移动,就从前开始执行移动的操作
- 往后移动,就从后面开始执行移动的操作
反之,会待移动的数据覆盖
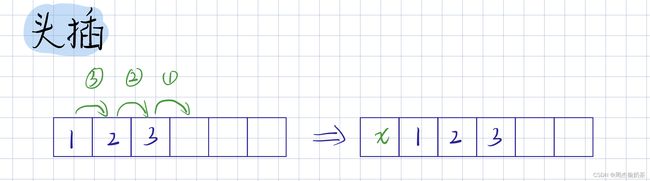
头插
思路:全部元素往后移动,arr[0] = x
- 头插,要把数据往后挪,所以从后面开始操作
void SLPushFront(SL* psl, SLDataType x)
{
assert(psl);
CheckCapacity(psl);
int end = psl->size - 1;
while (end >= 0)
{
//1.初始操作:arr[size] = arr[size-1]
//2.结束操作:arr[1] = arr[0]
psl->arr[end + 1] = psl->arr[end];
end--;
}
psl->arr[0] = x;
psl->size++;
}
- 增加数据要检查容量
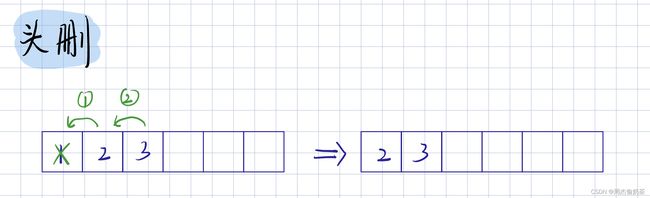
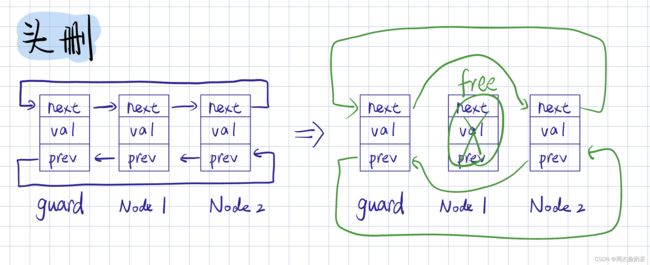
头删
思路:从arr[1]到arr[size-1],全部往前移动,覆盖掉arr[0]
-
头删数据往前移,所以从前开始操作
-
移动操作:arr[i] = arr[i + 1]
-
写出边界值的操作,更清晰:arr[0] ~ arr[size-2] = arr[1] ~ arr[size-1]
-
void SLPopFront(SL* psl)
{
assert(psl);
assert(psl->size > 0);
int begin = 0;
while (begin <= psl->size - 2)
{
//1.初始操作:arr[0] = arr[1]
//2.结束操作:arr[size-2] = arr[size-1]
psl->arr[begin] = psl->arr[begin + 1];
begin++;
}
psl->size--;
}
-
删除数据,表不能为空
-
为什么没有 arr[size-1] = arr[size]?要删掉的数据你还往前移啥呀,直接size–,干掉
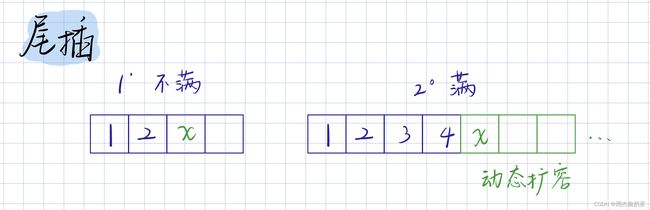
尾插
void SLPushBack(SL* psl, SLDataType x)
{
assert(psl);
CheckCapacity(psl);
psl->arr[psl->size] = x;
psl->size++;
}
- 增加数据要检查容量
尾删
思路:size–,直接干掉
void SLPopBack(SL* psl)
{
assert(psl);
assert(psl->size > 0);
psl->size--;
}
- 删除数据,表不能为空
查找
思路:遍历
int SLFind(SL* psl, SLDataType x)
{
assert(psl);
int i = 0;
for (i = 0; i < psl->size; i++)
{
if (psl->arr[i] == x)
return i;
}
return -1;
}
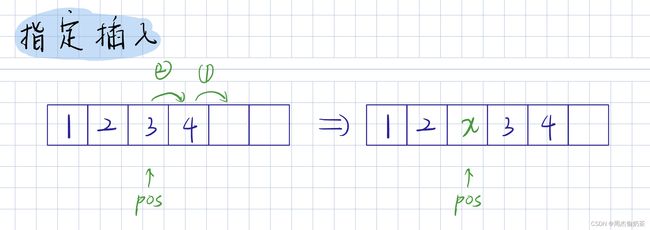
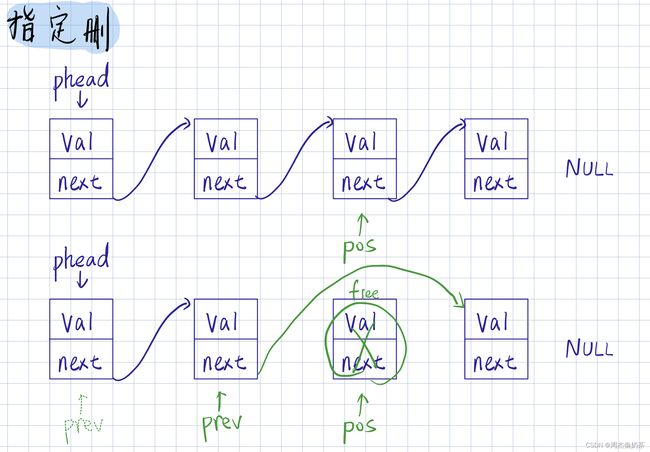
指定插入
思路:arr[pos] ~ arr[size-1] 移动到 arr[pos+1] ~ arr[size],完成挪动
-
往后移动,从后面开始操作
-
移动操作:arr[i + 1] = arr[i]
-
写出边界值的操作,更清晰:arr[pos+1] ~ arr[size] = arr[pos] ~ arr[size-1]
-
void SLInsert(SL* psl, int pos, SLDataType x)
{
assert(psl);
assert(pos <= psl->size);
CheckCapacity(psl);
int end = psl->size - 1;
while (end >= pos)
{
psl->arr[end + 1] = psl->arr[end];
end--;
}
psl->arr[pos] = x;
psl->size++;
}
-
pos要合法:下标不能超过size,下标为size的时候就是尾插
- pos == 0,就是头插
- pos == size,就是尾插
-
增加数据,要检查容量
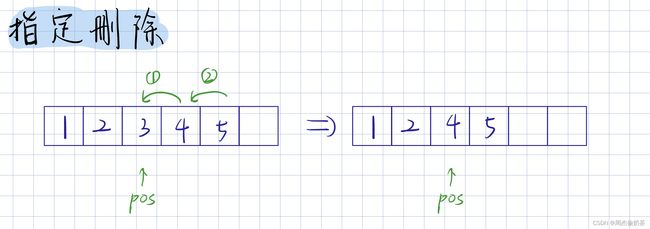
指定删除
思路:arr[pos+1] ~ arr[size-1] 移动到 arr[pos] ~ arr[size-2],完成覆盖
-
往前移动,移动后相对位置是前面
-
移动操作:arr[i] = arr[i + 1]
-
写出边界值的操作,更清晰:arr[pos] ~ arr[size-2] = arr[pos+1] ~ arr[size-1]
-
void SLErase(SL* psl, int pos)
{
assert(psl);
assert(pos < psl->size);
assert(psl->size > 0);
int begin = pos;
while (begin <= psl->size - 2)
{
psl->arr[begin] = psl->arr[begin + 1];
begin++;
}
psl->size--;
}
-
pos要合法:下标不能超过size-1,下标为size的位置没有数据
-
删除数据,不能为空
-
pos == 0,就是头删;pos == size-1,就是尾删
解惑2 像尾删这种这么简单的操作,还要封装成函数,不是多此一举吗?
其实还是 “高内聚,低耦合” 的事儿,如果直接操作顺序表内的数据,你这时候写出来的操作顺序表数据的代码,可复用吗?顺序表元素换一下,又或者别的底层实现动了,你的代码就被废掉…
1.1.2 顺序表的优劣
优势:
- 尾部操作效率高
- 能够直接访问任意元素,O(1)
- 缓存利用率高
劣势:
- 容量问题
- 开多可能浪费
- 扩容,原地扩还好,异地扩损耗大
- 任意位置的增删操作效率低(要挪动元素)
1.2 单向链表
:一种线性表,物理结构上不连续
链表可以解决顺序表的容量问题:按需开辟,不会浪费空间
逻辑结构:
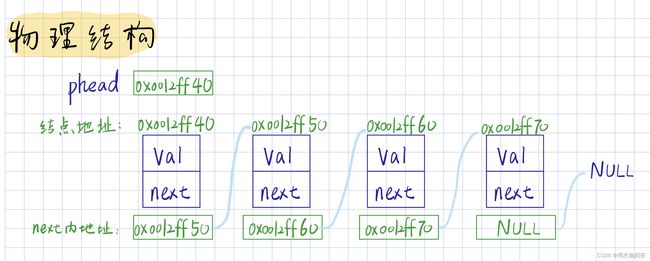
物理结构:
1.2.1 实现&分析
类型声明
typedef int SListDataType;
typedef struct SListNode
{
SListDataType val;
struct SListNode* next;//下一个结点的地址
}SLNode;
- val:链表内结点中保存的值
- next:后继结点的地址,是链表中的“链条”
- 结构体指针的定义需要注意:
接口声明
void SLDestroy(SLNode** pphead);
void SLPrint(SLNode* phead);
SLNode* BuyNode(SListDataType x);
void SLPushFront(SLNode** pphead, SListDataType x);
void SLPopFront(SLNode** pphead);
void SLPushBack(SLNode** pphead, SListDataType x);
void SLPopBack(SLNode** pphead);
SLNode* SLFind(SLNode* phead, SListDataType x);
//在pos前插入
void SLInsert(SLNode** pphead, SLNode* pos, SListDataType x);
//在pos后插入
void SLInsertAfter(SLNode** pphead, SLNode* pos, SListDataType x);
//删除pos
void SLErase(SLNode** pphead, SLNode* pos);
解疑1:为什么有的接口,参数要设计成二级指针?
- 因为有的接口需要修改传过来的 链表头指针(要改什么数据,就需要什么数据的指针)
- 有时也是为了保持接口一致性
接口测试
#include "SList.h"
void test1()
{
SLNode* plist = NULL;
SLPushFront(&plist, 1);
SLPushFront(&plist, 2);
SLPushFront(&plist, 3);
SLPushFront(&plist, 4);
SLPrint(plist);
SLPopFront(&plist);
SLPopFront(&plist);
SLPopFront(&plist);
SLPopFront(&plist);
SLPrint(plist);
SLPushBack(&plist, 10);
SLPushBack(&plist, 20);
SLPushBack(&plist, 30);
SLPushBack(&plist, 40);
SLPrint(plist);
SLPopBack(&plist);
SLPopBack(&plist);
SLPopBack(&plist);
SLPopBack(&plist);
SLPrint(plist);
SLDestroy(&plist);
}
void test2()
{
SLNode* plist = NULL;
SLPushFront(&plist, 400);
SLPushFront(&plist, 300);
SLPushFront(&plist, 200);
SLPushFront(&plist, 100);
SLPrint(plist);
SLNode* pos = SLFind(plist, 100);
//SLNode* pos = SLFind(plist, 400);
//pos->val = 123;
//SLPrint(plist);
//SLInsert(&plist, pos, 999);
SLInsertAfter(&plist, pos, 666);
SLPrint(plist);
pos = SLFind(plist, 400);
SLErase(&plist, pos);
SLPrint(plist);
SLDestroy(&plist);
}
int main()
{
//test1();
test2();
return 0;
}
功能接口实现
解疑1:为什么单链表没有初始化接口?
单链表的初始状态就是一个值为空的头指针,没什么好初始化的了
销毁
思路:用cur来遍历链表,逐个释放,最后置空*pphead(传过来的是链表头指针地址,所以解引用后置空)
void SLDestroy(SLNode** pphead)
{
assert(pphead);
SLNode* cur = *pphead;
while (cur)
{
SLNode* next = cur->next;
free(cur);
cur = next;
}
*pphead = NULL;
}
- 销毁:链表中的Node都是malloc出来的,要free,防止内存泄漏
打印
思路:用cur来遍历链表,逐个打印
void SLPrint(SLNode* phead)
{
SLNode* cur = phead;
while (cur)
{
printf("[%d]->", cur->val);
cur = cur->next;
}
printf("[NULL]\n");
}
- 打印:一般都创建一个cur指针来遍历,以防找不到头
解疑2:Destroy 和 Print 中,都能看到 cur = cur->next 的操作,这是啥意思?
所谓cur = cur->next ,就是把cur指针内存的地址换成下一个node的地址,这时候对cur解引用,就可以找到下一个node了
解疑3:为什么Print不用assert(phead)?
为空就不打印数据或是打印一个NULL,没必要直接阻断程序
创建新结点
SLNode* BuyNode(SListDataType x)
{
SLNode* newnode = (SLNode*)malloc(sizeof(SLNode));
if (newnode == NULL)
{
perror("BuyNode:malloc");
exit(-1);
}
newnode->next = NULL;
newnode->val = x;
return newnode;
}
解疑4:为什么创建新结点要malloc?
- 栈空间本来就不大
- 在局部创建结点,再返回其地址…返回栈空间地址…挫
增删查改接口实现
头插
思路:创建新结点newnode,,后链接*pphead->next,并把head改成newnode
- 空链表:创建新节点newnode,*pphead 指向 newnode,代码可用
void SLPushFront(SLNode** pphead, SListDataType x)
{
assert(pphead);
SLNode* newnode = BuyNode(x);
newnode->next = *pphead;
*pphead = newnode;
}
- pphead为空没法访问到链表
- 空链表情况:代码可用
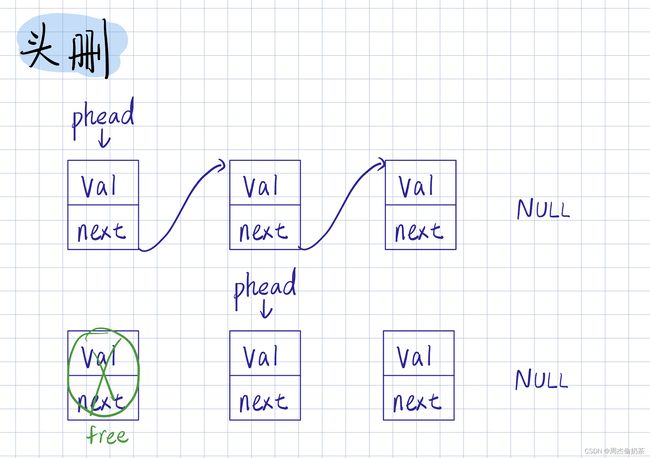
头删
思路:*pphead直接指向*pphead->next,释放头结点
void SLPopFront(SLNode** pphead)
{
assert(pphead);
assert(*pphead);
SLNode* del = *pphead;
*pphead = (*pphead)->next;
free(del);
}
- pphead为空没法访问链表
- *pphead为空,即是表为空,无法删除
- malloc 的 node 要 free
- 只有一个结点:代码可用
尾插
思路:找尾结点tail,创建新结点newnode,tail链接newnode
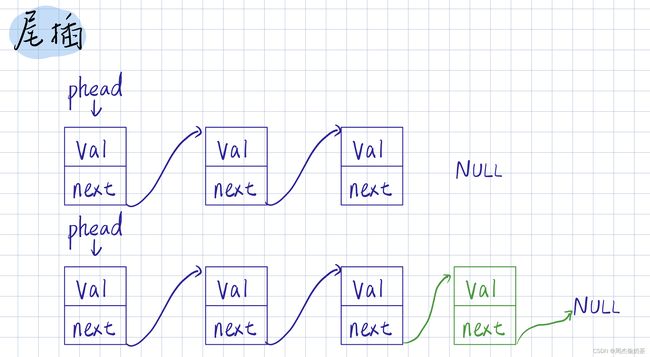
- 空链表:没法找尾结点,直接创建新节点newnode,让*pphead 指向 newnode,
void SLPushBack(SLNode** pphead, SListDataType x)
{
assert(pphead);
SLNode* newnode = BuyNode(x);
if (NULL == *pphead)
{
*pphead = newnode;
}
else
{
SLNode* tail = *pphead;
while (tail->next)
{
tail = tail->next;
}
tail->next = newnode;
}
}
- pphead为空没法访问链表
尾删
思路:找到尾结点的前驱结点 prev, prev->next = NULL,释放尾结点
void SLPopBack(SLNode** pphead)
{
assert(pphead);
assert(*pphead);
if ((*pphead)->next == NULL)
{
free(*pphead);
*pphead = NULL;
}
else
{
SLNode* prev = *pphead;
while (prev->next->next)
{
prev = prev->next;
}
SLNode* del = prev->next->next;
prev->next = NULL;
free(del);
}
}
- pphead为空没法访问链表
- *pphead为空,即是表为空,无法删除
- malloc 的 node 要 free
- 只有一个结点:直接置空头指针
查找
思路:遍历
SLNode* SLFind(SLNode* phead, SListDataType x)
{
assert(phead);
SLNode* cur = phead;
while (cur)
{
if (x == cur->val)
return cur;
else
cur = cur->next;
}
return NULL;
}
- 最好拷贝phead为cur,用cur遍历
- 链表中的位置只能通过指针确定,不能用顺序表那样int来作为下标
指定前插
思路:找到pos的前驱结点prev, 创建新结点newnode,前链接prev,后链接pos

//在pos前插入
void SLInsert(SLNode** pphead, SLNode* pos, SListDataType x)
{
assert(pphead);
assert(pos);
if (pos == *pphead)
{
SLPushFront(pphead, x);
}
else
{
SLNode* newnode = BuyNode(x);
SLNode* prev = *pphead;
while (prev->next != pos)
{
prev = prev->next;
assert(prev);//检查pos合法性
}
newnode->next = pos;
prev->next = newnode;
}
}
- pphead为空没法访问链表
- pos为空非法
- 单链表一般 先链接newnode和其后继结点, 再链接前驱结点
- 链接:用prev找pos,再链接
- 按顺序链接:先链接后继结点,再链接前驱结点
- 不按顺序链接:创建prev,得到prev–>newnode–>pos
- *pos == pphead : 头插
- 找pos:循环中必须断言,来检查pos的合法性(如果不合法还不断言,就会死循环)
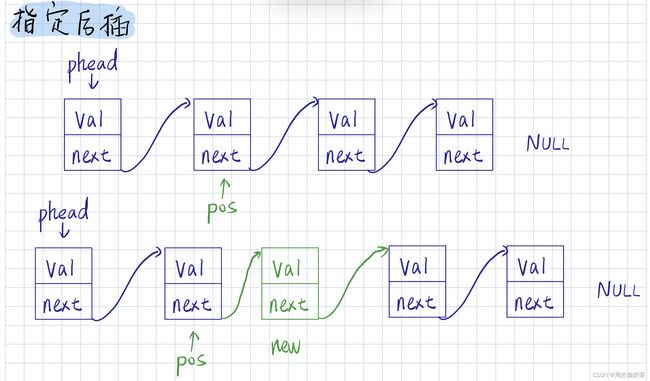
指定后插
思路:创建新结点newnode,前链接pos,后链接pos->next
//在pos后插入
void SLInsertAfter(SLNode** pphead, SLNode* pos, SListDataType x)
{
assert(pphead);
assert(pos);
SLNode* newnode = BuyNode(x);
newnode->next = pos->next;
pos->next = newnode;
}
- pphead为空没法访问链表
- pos为空非法
- *pos == pphead : 代码可用
指定删
思路:找到pos的前驱结点prev, prev指向pos->next,释放pos
//删除pos
void SLErase(SLNode** pphead, SLNode* pos)
{
assert(pphead);
assert(*pphead);
assert(pos);
if (*pphead == pos)
{
SLPopFront(pphead);
}
else
{
SLNode* del = pos;
SLNode* prev = *pphead;
while (prev->next != pos)
{
prev = prev->next;
assert(prev);
}
prev->next = pos->next;
free(del);
}
}
- pphead为空没法访问链表
- *pphead为空,即是表为空,无法删除
- malloc 的 node 要 free
- 只有一个结点:调用头删
- 找pos:要断言检查pos合法性
接口实现总结:
-
边界情况:
- 全部接口(除删除):考虑空链表情况,可以先写出普通情况,再套空链表情况,不行就另写空表的代码
- 删除:考虑只有一个结点
- 需要找pos的接口:
- 循环内要断言,检查pos合法性
- 考虑pos == head
-
链接:只要遵循 “待使用不改变” 即可
- 不另用空间:一般先链接后继结点,再链接前驱结点
- 另开空间:按需要创建 prev/next/tail 来辅助完成链接
1.2.2 单链表的优劣
优势:
- 头操作效率高
- 空间按需开辟,不会浪费
- 任意位置插入效率高(只需要链接)
- 在链表中结构最简单,能作其他数据结构的子结构
劣势:
- 中部尾部操作效率低
- 频繁malloc,造成内存碎片
- 无法随机访问,O(N)
- 实现过程中总是要考虑 第一个结点、空链表 的情况,改head还要二级指针,麻烦
- 缓存利用率低
1.3 带头双向循环链表
这个看上去比较复杂的链表,才真正解决了顺序表的问题。虽然逻辑结构看着复杂点,但用起来真是非常爽
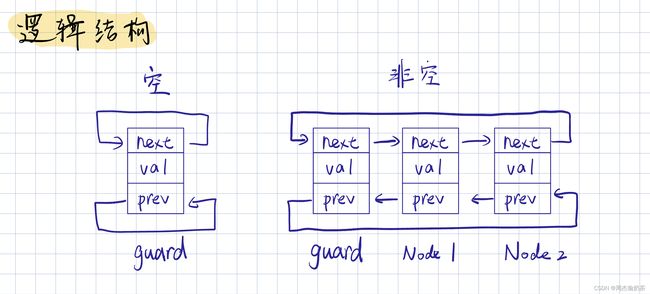
那么,什么是带头,什么是双向,什么是循环?
- 带头:链表带一个 哨兵头结点 guard,它指向链表的第一个有效结点
- 双向:链表中任意一个结点,都能找到其 前驱结点 和 后继结点
- 循环:链表尾的next指向链表头,链表头的prev指向链表尾
^前驱结点:前一个结点
^后继结点:后一个结点
逻辑结构如图:
1.3.1 实现&分析
工程创建
我们还是采用以前通讯录类似的 接口实现、接口声明、测试接口,三大块的逻辑来创建工程:
- LinkedLIst.h:声明类型、接口等,包含实现接口要用的头文件
- LinkedList.c:实现接口
- test.c:测试接口
类型声明
typedef int ListDataType;
typedef struct ListNode
{
ListDataType val;
struct ListNode* next;
struct ListNode* prev;
}ListNode;
- val:存值
- next:保存后继结点的地址
- prev:保存前驱结点的地址
接口声明
#include 哨兵头的好处就体现出来了:
所有改头指针的情况都不需要考虑了——所有“头部操作/尾部操作”都转成 “中部操作”,永远有一个挺拔的guard站在那,为我们保驾护航。
我们也不再需要传二级指针啦。
功能接口实现
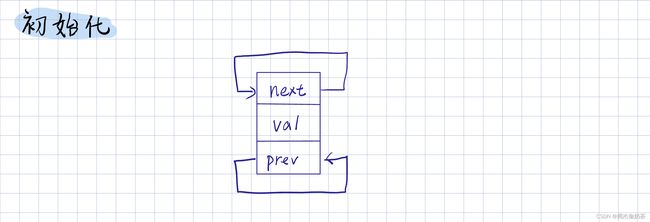
初始化
思路:创建一个哨兵头结点 guard, 并使它自循环(这样就能直接链接)
ListNode* ListInit()
{
ListNode* guard = BuyNode(0);
guard->next = guard;
guard->prev = guard;
return guard;
}
解惑1 下面定义的BuyNode能在上面的ListInit用?
:调用函数的条件
- 在调用的位置前有声明
- 在调用的位置前有定义
咱们顶上包含了头文件嘛!
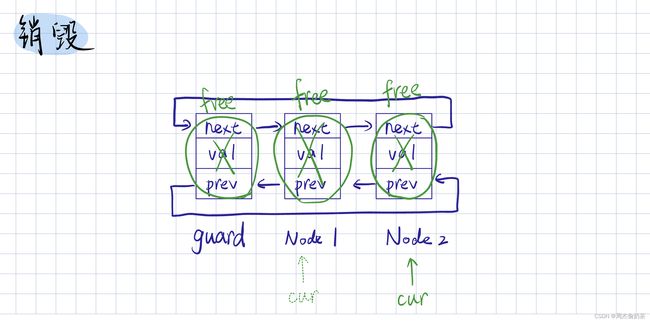
销毁
思路:用一个临时指针,从phead->next(phead接收的是guard,guard->next开始才是有效数据)开始遍历,每次保存next,释放cur
void ListDestroy(ListNode* phead)
{
assert(phead);
ListNode* cur = phead->next;
while (cur != phead)
{
ListNode* next = cur->next;
free(cur);
cur = next;
}
free(phead);
}
- 遍历:循环链表的遍历就不能用 cur != NULL 了,它可没有一个结点指向空。根据特性,当 cur==head,遍历就结束了
- 最后别忘了释放guard
打印
void ListPrint(ListNode* phead)
{
assert(phead);
ListNode* cur = phead->next;
while (cur != phead)
{
printf("[%d] <-> ", cur->val);
cur = cur->next;
}
printf("[NULL]\n");
}
思路:遍历,同上
创建新结点
思路:在堆上动态开辟空间创建结点,并初始化
ListNode* BuyNode(ListDataType x)
{
ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
if (newnode == NULL)
{
perror("BuyNode:malloc");
exit(-1);
}
else
{
newnode->val = x;
newnode->next = NULL;
newnode->prev = NULL;
return newnode;
}
}
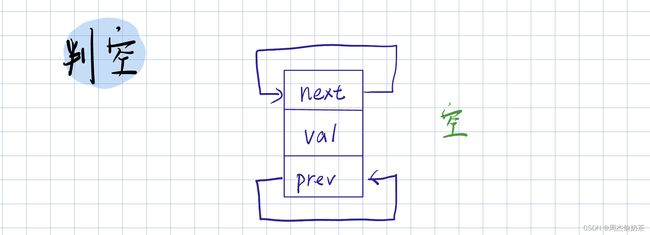
判空
思路:phead->next指向自己的时候就是空——为空返回真,不为空返回假
bool ListEmpty(ListNode* phead)
{
return phead->next == phead;
}
计算大小
思路:遍历链表,计算大小
size_t ListSize(ListNode* phead)
{
assert(phead);
size_t cnt = 0;
ListNode* cur = phead;
while (cur != phead)
{
cnt++;
cur = cur->next;
}
return cnt;
}
增删查改接口实现
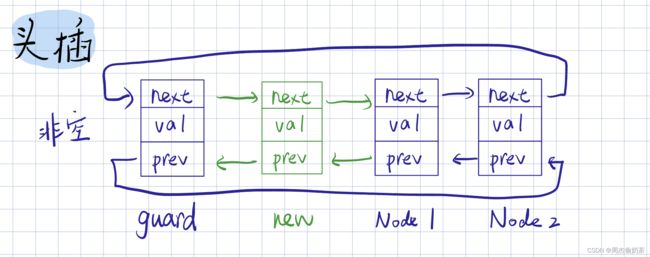
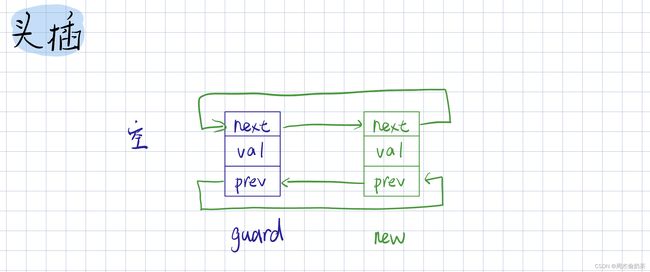
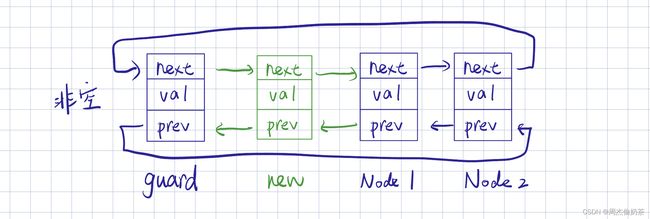
头插
思路:创建新结点,前链接 guard,后链接 guard->next
- 空链表:代码也可用
- 直接实现
void ListPushFront(ListNode* phead, ListDataType x)
{
assert(phead);
ListNode* newnode = BuyNode(x);
newnode->next = phead->next;
phead->next->prev = newnode;
phead->next = newnode;
newnode->prev = phead;
}
- 调用指定插
void ListPushFront(ListNode* phead, ListDataType x)
{
assert(phead);
ListInsert(phead->next, x);
}
见下文
头删
思路:guard直接指向第二个有效结点,把第一个有效结点释放
- 空链表不能删了
- 直接实现
void ListPopFront(ListNode* phead)
{
assert(phead);
assert(!ListEmpty(phead));
ListNode* first = phead->next;
ListNode* second = first->next;
phead->next = second;
second->prev = phead;
free(first);
}
- 调用指定删
void ListPopFront(ListNode* phead)
{
assert(phead);
ListErase(phead->next);
}
见下文
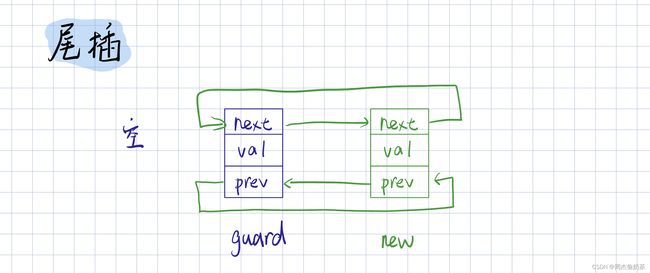
尾插
思路:创建新结点,前链接 guard->prev ,后链接 guard
- 直接实现
void ListPushBack(ListNode* phead, ListDataType x)
{
assert(phead);
ListNode* newnode = BuyNode(x);
ListNode* tail = phead->prev;
tail->next = newnode;
newnode->prev = tail;
newnode->next = phead;
phead->prev = newnode;
}
- 调用指定插
void ListPushBack(ListNode* phead, ListDataType x)
{
assert(phead);
ListInsert(phead, x);
}
尾删
思路:拿一个 tail 指向尾结点,再拿一个 prev 保存尾结点的前驱结点,链接 prev 和 guard
- 空链表:不能删
- 直接实现
void ListPopBack(ListNode* phead)
{
assert(phead);
assert(!ListEmpty(phead));
ListNode* tail = phead->prev;
ListNode* prev = tail->prev;
prev->next = phead;
phead->prev = prev;
free(tail);
}
- 调用指定删
void ListPopBack(ListNode* phead)
{
assert(phead);
ListErase(phead->prev);
}
查找
思路:遍历
ListNode* ListFind(ListNode* phead, ListDataType x)
{
assert(phead);
ListNode* cur = phead->next;
while (cur != phead)
{
if (cur->val == x)
return cur;
else
cur = cur->next;
}
return NULL;
}
指定前插
思路:用 prev 保存 pos 的上一个,创建新结点,前链接 prev, 后链接 pos
- 当 pos == guard:在pos前,也就是guard->prev 前插入,就是尾插
- 当 pos == guard->next:在pos前,也就是第一个结点前插入,也就是头插
void ListInsert(ListNode* pos, ListDataType x)
{
assert(pos);
ListNode* newnode = BuyNode(x);
ListNode* prev = pos->prev;
prev->next = newnode;
newnode->prev = prev;
newnode->next = pos;
pos->prev = newnode;
}
指定删
思路:用 prev 保存 pos->prev,用 next 保存 pos->next,链接 prev 和 next
- 当 pos == guard->prev:尾删
- 当 pos == guard->next:头删
void ListErase(ListNode* pos)
{
assert(pos);
ListNode* prev = pos->prev;
ListNode* next = pos->next;
prev->next = next;
next->prev = prev;
free(pos);
}
1.3.2 带头双向链表的优化
实现完带头双向循环链表,可以切实体会到它相较于单向链表的优势了:
- 带头:免去很多对空链表的特殊处理
- 双向:很少需要遍历来找结点了
- 循环:尾操作方便
1.3.3 带头双向链表的优劣
优势:
- 头部操作、尾部操作效率高
- 空间按需开辟,不会浪费
- 任意位置插入效率高(只需要链接)
- 使用方便
劣势:
- 无法随机访问,O(N)
- 频繁malloc,造成内存碎片
- 缓存利用率低
2. 顺序表和链表对比
这里的链表指的是带头双向循环链表
| 区别 | 顺序表 | 链表 |
|---|---|---|
| 存储模式 | 连续存储 | 非连续存储 |
| 能否随机访问 | 可以,O(1) | 不适合,O(N) |
| 空间损耗 | 容易浪费 | 节省空间 |
| 任意位置的增删操作 | 效率低,要挪动元素 | 效率高,只需改变指针 |
| 缓存利用率 | 高 | 低 |
| 应用场景 | 元素高效存储+频繁访问 | 频繁的任意位置的增删 |
缓存利用率
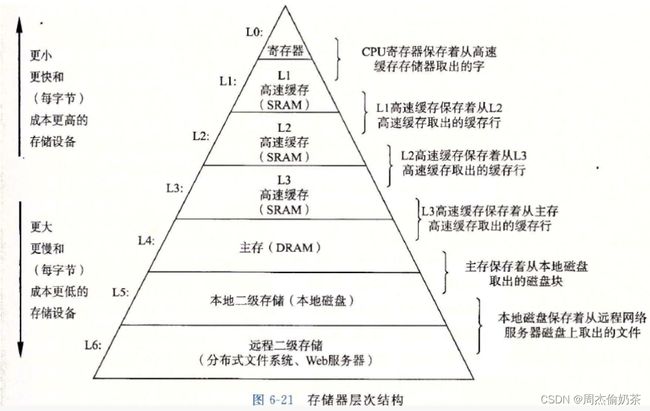
为什么出现缓存?
:cpu的速度比内存快太多,如果cpu计算时直接从内存中访问数据,就容易出现“cpu算完没事干,只能等内存拿数据给它”的情况,所以大佬们设计了高速缓存。
有了高速缓存,cpu又是怎么拿数据的?
:cpu每次访问数据,都从缓存中找
- 找到数据,这一行为称 “缓存命中”
- 没找到数据,也就是 “未命中”
根据我们访问数据的习惯(访问一个数据,通常也要访问周围的数据,而且要是一个个数据读也太挫了),产生了局部性原理。
局部性原理
:高速缓存从内存中读取数据的时候,会把要访问的数据局部的一整块数据读取过来
局部性原理对我们理解缓存利用率有什么用呢?
缓存依这种原理,产生新的拿取数据的方式:
- 绿色部分是要访问的数据,而红色部分是额外拿取的数据
- 可以看到,顺序表在内存中连续存储,此时若要访问表内其他元素,就能够通过额外拿取的数据直接 命中
- 而链表是动态开辟,在内存中不是连续存储,此时若要访问表内其他元素,就不能直接 命中, 而且还会造成 缓存污染和缓存空间浪费
^缓存污染: 加载一大块数据,只有很小一块有用,其他的数据就“污染”了缓存。
^缓存空间浪费: 缓存空间很小,更多数据进入,就会相应有先前进来的数据被挤出去
缓存命中率
:简单来说,这里的情况就是,cpu对缓存中连续数据的访问命中的概率
缓存命中率高,自然效率就会高很多,如果命中率不高,每次加载一大块数据都是白加载,这样还会造成“缓存污染”,和缓存空间的浪费
- 上图的顺序表,缓存命中率自然比链表高得多,效率也高,这也是为什么,单纯存储数据还是建议用顺序表
本期分享就到这啦,不足之处望请斧正