【刷题笔记】--dp--01背包

经典例题：给出n个物品的重量和价值，然后还给出背包的最大容量，让你计算背包能装下的最大价值。

已知题目给出：

    int n=4;//表示有4个物品
	int weight[]={2,3,4,5};
	int value[]={3,4,5,8};
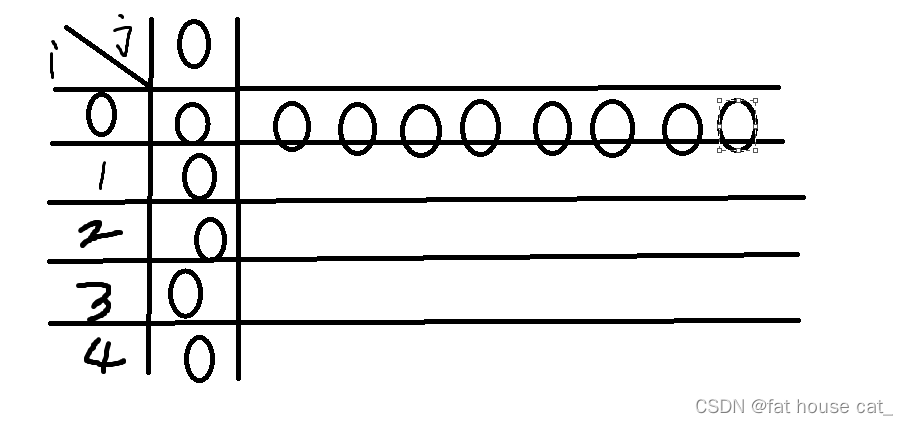
	int maxcapacity=8;

思路：设一个二维的dp数组：dp[i][j]表示在 i 个物品和 背包的容量j下的背包最大价值。

我们现在要求的是这4个物品，8的背包容量下的最大值，这是原问题，也就是求dp[4][8]然后我们要想子问题怎么表示出这个原问题。

①dp[4][8]是不是可以表示成dp[3][8]（如果第四个物品没装，背包容量还有8的价值）or 表示成

dp[3][3]（如果第四个物品装，背包容量还有3的情况下的价值），因为要的是最大价值，所以我们在这两种选择下取最大值。

②但如果背包容量小于要装的物品的重量时，我们是不是不能把该物品装进背包里，所以只能是上述不装的情况。

所以通过上述分析就找到了原问题与子问题的关系。

然后就是初始化的问题，

代码：

//0-1背包问题
#include

int max(int a,int b){
	if(a>b){
		return a;
	}
	return b;
}

int main(){
	int n=4;//表示有4个物品
	int weight[]={0,2,3,4,5};
	int value[]={0,3,4,5,8};
	int maxcapacity=8;
	int i,j;
	int dp[100][100]={0};
	for(i=1;i<=n;i++){
		for(j=1;j<=maxcapacity;j++){
			if(weight[i]>j){
				dp[i][j]=dp[i-1][j];
			}
			else{
				dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
			}
		}
	}
	printf("%d",dp[n][maxcapacity]);
	return 0;
} 

---

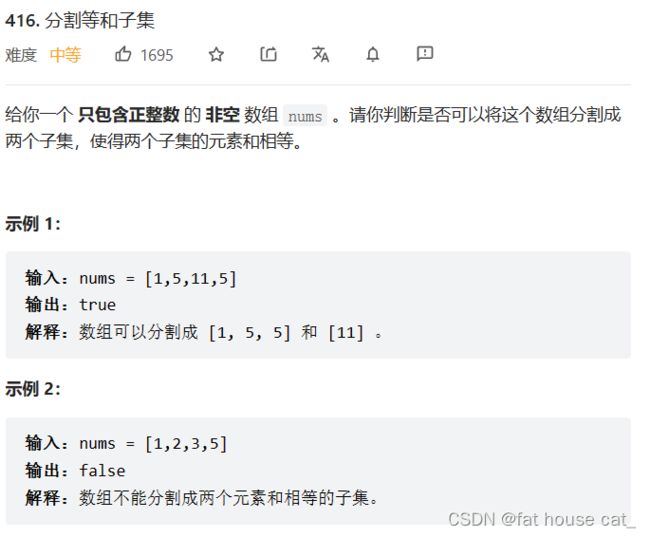
类似地，还有这道题也是差不多思路：

思路：这道题dp[i][j]表示前i+1个nums数组里的元素 是否能构成分割成两个元素和相等的子集（元素和为j）。

我们现在要求的是dp[3][11]的值（只有两种：1 or 0） 

①dp[3][11]是不是可以表示为dp[2][11]的01情况（nums[3]不取，target值不变）或者dp[2][6]的01情况（nums[3]取，target值减去nums[3]的值）。

②但也要考虑一种情况，就是nums[3]如果比target值大，一定不取。

然后就是初始化问题，如下：

 代码：

int max(int a,int b){
    if(a>b){
        return a;
    }
    return b;
}
bool canPartition(int* nums, int numsSize){
    if(numsSize<2){
        return false;
    }
    int sum=0;
    int maxNum=0;
    int i,j;
    for(i=0;itarget){
        return false;
    }
    int dp[numsSize][target+1];
    memset(dp,0,sizeof(dp));
    for(i=0;i=nums[i]){
                dp[i][j]=dp[i-1][j]||dp[i-1][j-nums[i]];
            }
            else{
                dp[i][j]=dp[i-1][j];
            }
        }
    }
    return dp[numsSize-1][target];
}

---

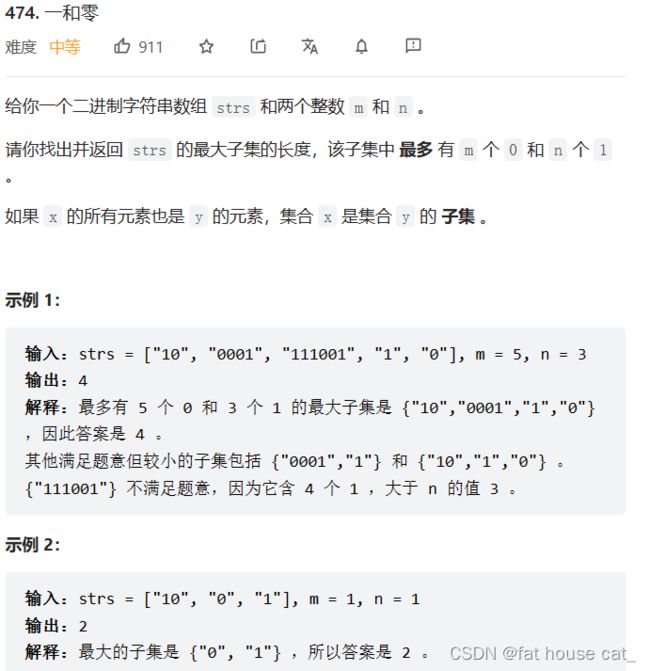
题目三：474. 一和零 

思路：这道题是标准的01背包题，把数组里的每个字符串看作物品，m和n看作背包能容量的最大限度，我们的目标就是求能往背包里装物品的数量的最大值。 

一样的，会有两种情况出现。

①背包容量不够，不装当前物品，即m

dp[i][j][k]=dp[i-1][j][k];（这一步也是每次循环都必备的），不管背包容量够不够

②背包容量够，可以选择装或不装

dp[i][j][k]=fmax(  dp[i][j][k]  ,  dp[i-1][j-zerosOnes[0]][k-zerosOnes[1]]+1  );（别忘了这个+1，表示装进这个物品后，背包里物品数量加1。）

然后就是初始化问题，当物品为0个时，不管n和m为何值，dp[0][j][k]都为0。所以我们从i=1开始遍历，j和k从0开始遍历，因为当i=1时我们并没有给初始化。

 代码：

void getzerosOnes(int zerosOnes[],char strs[]){
    int length=strlen(strs);
    int i;
    for(i=0;i=zeros&&k>=ones){
                    dp[i][j][k]=fmax(dp[i][j][k],dp[i-1][j-zerosOnes[0]][k-zerosOnes[1]]+1);
                }
              
            }
        }
    }
    return dp[strsSize][m][n];
}

题目四：1049. 最后一块石头的重量 II 

思路： 

 要使剩下的最后一块石头重量最小，就是将全部石头分成势均力敌的两堆，即分成重量差不多的两堆，也就是这两堆每堆重量接近sum/2.然后将这两堆重量相减即为剩下的最后一块石头的最小的重量。

代码：

int lastStoneWeightII(int* stones, int stonesSize){
    int i,sum=0,j;
    for(i=0;i=stones[i-1]){
                dp[i][j]=fmax(dp[i-1][j],dp[i-1][j-stones[i-1]]+stones[i-1]);
            }
            else{
                dp[i][j]=dp[i-1][j];
            }
        }
    }
    return sum-dp[stonesSize][capacity]-dp[stonesSize][capacity];
}