【一起啃书】《机器学习》第三章 线性模型

第三章 线性模型

3.1 基本形式

  给定由$d$个属性描述的示例$\mathbf{x}=(x_1;x_2;...;x_d)$，其中$x_i$是$\mathbf{x}$在第$i$个属性上的取值，线性模型试图学得一个通过属性的线性组合来进行预测的函数，如下所示：
$$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$$
  线性模型形式简单、易于建模，因此线性模型有很好的可解释性。

3.2 线性回归

  给定数据集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),...,({\mathbf{x}}_m,y_m)\}$，其中${\mathbf{x}}_i=(x_{i1};x_{i2};...;x_{id}),y_i\in \mathbb{R}$。“线性回归”试图学得一个线性模型以尽可能准确地预测实值输出标记。均方误差是回归任务中最常用的性能度量，因此在回归任务中通常试图让均方误差最小化，如下：
$$(w^{\ast },b^{\ast })=\underset{(w,b)}{\mathrm{argmin}}\sum _{i=1}^m{(f(x_i)-y_i)}^2$$
  均方误差对应了常用的欧几里得距离（欧氏距离），基于均方误差最小化来进行模型求解的方法称为最小二乘法。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小，对于上面的这个式子，我们分别对$w$和$b$求导并令对应的偏导数等于0，即可得到最优解如下：
$$w=\frac{\sum _{i=1}^m{y}_i(x_i-\overline{x})}{\sum _{i=1}^m{x}_i^2-\frac{1}{m}{(\sum _{i=1}^m{x}_i)}^2},b=\frac{1}{m}\sum _{i=1}^m(y_i-w{x}_i)$$
  常见的还有多元线性回归（多个属性）、对数线性回归（输出为指数级变化）等。在多元线性回归中可能会解出来多组解，所以需要由学习算法的归纳偏好决定选择哪一个解作为输出，常见的做法是引入正则化项，以下为常用的$L_p$范数。

• L0范数是指向量中非零元素的个数。它的作用是可以提高模型参数的稀疏性，也就是让一些参数为零，从而减少特征的数量。

• L1范数是指向量中各个元素绝对值之和。它的作用也是可以提高模型参数的稀疏性，L1范数可以进行特征选择，即让特征的系数变为零。L1范数还可以作为正则化项，防止模型过拟合，提升模型的泛化能力。

• L2范数是指向量各元素的平方和然后求平方根。它的作用是减小模型所有参数的大小，可以防止模型过拟合，提升模型的泛化能力。L2范数会选择更多的特征，这些特征都会接近于零但不等于零，也可以作为正则化项，改善矩阵的条件数，加快收敛速度。

3.3 对数几率回归

  考虑到二分类任务，其输出标记$y \in { 0,1} $，而线性回归模型产生的预测值是实数值，所以需要将其进行转换，最理想的是单位阶跃函数，即预测值大于零判为正例，小于零判为负例，等于零可任意判别。但考虑到单位阶跃函数不连续，所以希望能找到在一定程度上近似单位阶跃函数的替代函数，并且单调可微，于是便有了对数几率函数。

  对数几率函数是一种Sigmoid函数，它将$z$值转化为一个接近0或1的$y$值，表达式为$y=\frac{1}{1+e^{-z}}$，换个形式也可写作$\ln \frac{y}{1-y}={\mathbf{w}}^T\mathbf{x}+b$，这里的$y$视为样本为正例的可能性，而$1-y$就是其反例可能性，所以$\frac{y}{1-y}$也叫做几率，$\ln \frac{y}{1-y}$就叫做对数几率，这种对应的线性回归模型就叫做对数几率回归，虽然叫做回归，但其实是一种分类方法。

  对于对数几率回归中$\mathbf{w}$和$b$的取值，可以采用极大似然法来进行估计。

3.4 线性判别分析

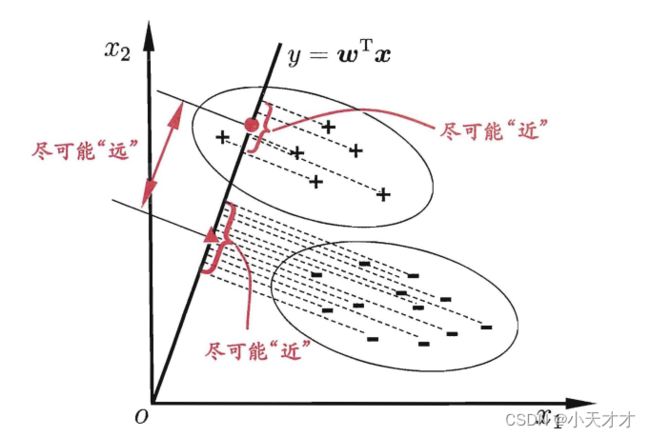
  线性判别分析是一种经典的线性学习方法，也叫作“Fisher判别分析”，主要思想是给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离，如下所示：

  给定数据集$D=\{({\mathbf{x}}_i,y_i){\}}_{i=1}^m,y_i=\{0,1\}$，两类样本的中心在直线上的投影为${\omega }^T{\mu }_0$和${\omega }^T{\mu }_1$，协方差为${\omega }^T{\mathbf{\Sigma }}_0\omega$和${\omega }^T{\mathbf{\Sigma }}_1\omega$，如果想使同类样例的投影点尽可能接近，则可以让协方差尽可能小；如果想使异类样例的投影点尽可能远离，则可以让类中心之间的距离 ∥ ω T μ 0 − ω T μ 1 ∥ \left\| {{{\bf{\omega }}^T}{{\bf{\mu }}_0} - {{\bf{\omega }}^T}{{\bf{\mu }}_1}} \right\| ​ωTμ0​−ωTμ1​ ​尽可能大。综合可得到以下最大化目标，可采用拉格朗日乘子法和奇异值分解求得最优解。
J = ∥ ω T μ 0 − ω T μ 1 ∥ 2 2 ω T Σ 0 ω + ω T Σ 1 ω J = \frac{{\left\| {{{\bf{\omega }}^T}{{\bf{\mu }}_0} - {{\bf{\omega }}^T}{{\bf{\mu }}_1}} \right\|_2^2}}{{{{\bf{\omega }}^T}{{\bf{\Sigma }}_0}{\bf{\omega }} + {{\bf{\omega }}^T}{{\bf{\Sigma }}_1}{\bf{\omega }}}} J=ωTΣ0​ω+ωTΣ1​ω ​ωTμ0​−ωTμ1​ ​22​​

3.5 多分类学习

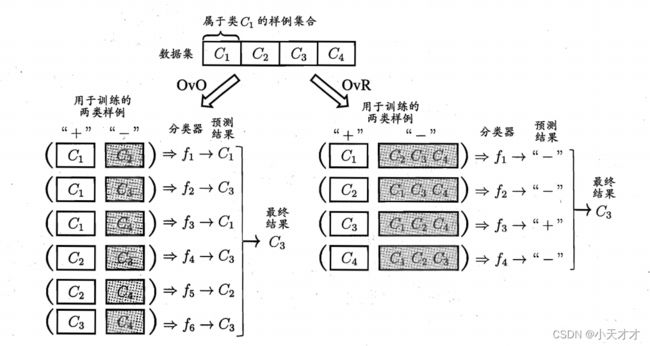
  多分类学习任务一般用拆解法来解决，最经典的拆分策略有三种：一对一（OvO）、一对其余（OvR）和多对多（MvM），一对一将N个类别两两配对，从而会产生N(N-1)/2个二分类任务；一对其余每次将一个类作为正例，剩下的作为反例，从而会产生N个二分类任务，这两种策略分别如下所示：

  而多对多就是每次将若干个类作为正类，若干个其他类作为反类，最常见的是纠错输出码（ECOC），该编码也有一定的容忍和修正能力，并且编码越长，纠错能力越强，共分为下面两步进行：

• 编码：对N个类别做M次划分，每次划分将一部分类别划为正类，一部分划为反类，从而形成一个二分类训练集；这样一共产生M个训练集，可训练出N个分类器。
• 解码：M个分类器分别对测试样本进行预测，这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测结果。

3.6 类别不平衡问题

  类别不平衡是指分类任务中不同类别的训练样例数目差别很大的情况，这种情况在现实的分类学习任务中很常见，一般可采用以下三种方法来解决：

• 欠采样：去除一些反例使得正、反例数目接近。
• 过采样：增加一些正例使得正、反例数目接近。
• 阈值移动：基于原始训练集进行学习，但在用训练好的分类器进行预测时，将$\frac{1-y^{\prime }}{y^{\prime }}=\frac{1-y}{y}\times \frac{m^{-}}{m^{+}}$嵌入决策过程中。

  需注意的是，欠采样法的时间开销通常远小于过采样法，因为前者丢弃了很多反例，使得分类器训练集远小于初始训练集，而过采样法增加了很多正例，其训练集大于初始训练集，过采样法也不能简单地对初始正例样本进行重复来样，否则会招致严重的过拟合。

3.7 逻辑回归为什么使用交叉熵而不是用均方差作为损失函数

  可以参考这篇文章【逻辑回归】，讲的很好！值得学习！