核主元分析 KPCA及matlab代码
前言
发现一篇很好的分享KPCA代码的文章
转载链接:
f核主元分析 (Kernel Principal Component Analysis , KPCA) – MATLAB中文论坛 (ilovematlab.cn)
原博主处有打包matlab代码
对于简单的数据降维,可参考:
用matlab实现kpca(核主成分分析法)_Bbei的博客-CSDN博客_matlabkpca
kpca思路和pca很像,可以了解 MATLAB实例:PCA(主成成分分析)详解_FDA_sq的博客-CSDN博客_matlab pca
KPCA简介
KPCA、PCA应用:
- 降维
- 特征提取
- 去噪
- 故障检测
假设训练数据由矩阵×表示,代表训练数据的大小,代表训练数据中特征向量的维度,KPCA具体实现过程如下:
Step1:利用核函数计算核矩阵=[]×
Step2:核矩阵的中心化
Step3:对中心化核矩阵进行特征值分解
Step4:特征向量的标准化
Step5:提取训练数据的主成分
Step6:提取测试数据的主成分KPCA的性能取决于核函数、核参数的选择。常用的核函数有线性核函数(Linear)、径向基(Radial Basis Function, RBF)和积分径向基(The Integrated Radial Basis Function, IRBF)核函数。当使用线性核函数时,KPCA退化为PCA。
主要功能
- 易于使用的 API
- 支持基于 KPCA 的数据降维、特征提取、数据重构
- 支持基于 KPCA 的故障检测和故障诊断
- 支持多种核函数 (linear, gaussian, polynomial, sigmoid, laplacian)
- 支持基于主元贡献率或给定数字的降维维度/主元个数选取
注意
- 仅支持基于高斯核函数的故障诊断
- 核函数的参数对KPCA 模型的性能影响很大
- 此代码仅供参考
使用说明
1. KPCA的建模过程(故障检测):
(1)获取训练数据(工业过程数据需要进行标准化处理)
(2)计算核矩阵
(3)核矩阵中心化
(4)特征值分解
(5)特征向量的标准化处理
(6)主元个数的选取
(7)计算非线性主成分(即降维结果或者特征提取结果)
(8)SPE和T2统计量的控制限计算
function model = kpca_train(X,options)
% DESCRIPTION
% Kernel principal component analysis (KPCA)
%
% mappedX = kpca_train(X,options)
%
% INPUT
% X Training samples (N*d)
% N: number of samples
% d: number of features
% options Parameters setting
%
% OUTPUT
% model KPCA model
%
%
% Created on 9th November, 2018, by Kepeng Qiu.
% number of training samples
L = size(X,1);
% Compute the kernel matrix
K = computeKM(X,X,options.sigma);
% Centralize the kernel matrix
unit = ones(L,L)/L;
K_c = K-unit*K-K*unit+unit*K*unit;
% Solve the eigenvalue problem
[V_s,D] = eigs(K_c/L);
lambda = diag(D);
% Normalize the eigenvalue
% V_s = V ./ sqrt(L*lambda)';
% Compute the numbers of principal component
% Extract the nonlinear component
if options.type == 1 % fault detection
dims = find(cumsum(lambda/sum(lambda)) >= 0.85,1, 'first');
else
dims = options.dims;
end
mappedX = K_c* V_s(:,1:dims) ;
% Store the results
model.mappedX = mappedX ;
model.V_s = V_s;
model.lambda = lambda;
model.K_c = K_c;
model.L = L;
model.dims = dims;
model.X = X;
model.K = K;
model.unit = unit;
model.sigma = options.sigma;
% Compute the threshold
model.beta = options.beta;% corresponding probabilities
[SPE_limit,T2_limit] = comtupeLimit(model);
model.SPE_limit = SPE_limit;
model.T2_limit = T2_limit;
end
2. KPCA的测试过程:
(1)获取测试数据(工业过程数据需要利用训练数据的均值和标准差进行标准化处理)
(2)计算核矩阵
(3)核矩阵中心化
(4)计算非线性主成分(即降维结果或者特征提取结果)
(5)SPE和T2统计量的计算
function [SPE,T2,mappedY] = kpca_test(model,Y)
% DESCRIPTION
% Compute the T2 statistic, SPE statistic,and the nonlinear component of Y
%
% [SPE,T2,mappedY] = kpca_test(model,Y)
%
% INPUT
% model KPCA model
% Y test data
%
% OUTPUT
% SPE the SPE statistic
% T2 the T2 statistic
% mappedY the nonlinear component of Y
%
% Created on 9th November, 2018, by Kepeng Qiu.
% Compute Hotelling's T2 statistic
% T2 = diag(model.mappedX/diag(model.lambda(1:model.dims))*model.mappedX');
% the number of test samples
L = size(Y,1);
% Compute the kernel matrix
Kt = computeKM(Y,model.X,model.sigma );
% Centralize the kernel matrix
unit = ones(L,model.L)/model.L;
Kt_c = Kt-unit*model.K-Kt*model.unit+unit*model.K*model.unit;
% Extract the nonlinear component
mappedY = Kt_c*model.V_s(:,1:model.dims);
% Compute Hotelling's T2 statistic
T2 = diag(mappedY/diag(model.lambda(1:model.dims))*mappedY');
% Compute the squared prediction error (SPE)
SPE = sum((Kt_c*model.V_s).^2,2)-sum(mappedY.^2 ,2);
end3. demo1: 降维、特征提取
(1) 源代码
% Demo1: dimensionality reduction or feature extraction
% ---------------------------------------------------------------------%
clc
clear all
close all
addpath(genpath(pwd))
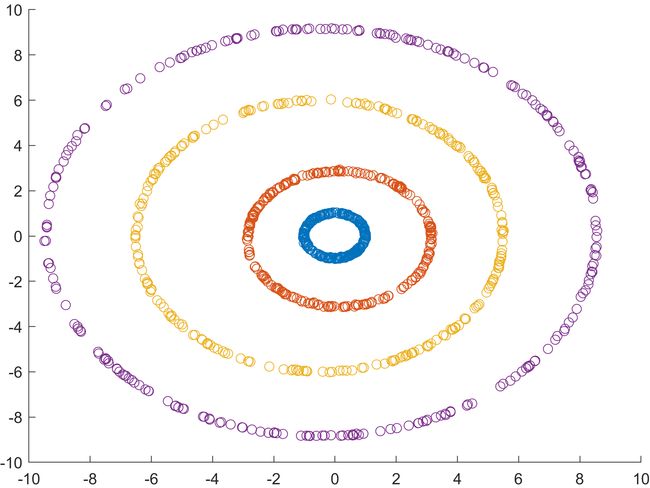
% 4 circles
load circledata
%
X = circledata;
for i = 1:4
scatter(X(1+250*(i-1):250*i,1),X(1+250*(i-1):250*i,2))
hold on
end
% Parameters setting
options.sigma = 5; % kernel width
options.dims = 2; % output dimension
options.type = 0; % 0:dimensionality reduction or feature extraction
% 1:fault detection
options.beta = 0.9; % corresponding probabilities (for ault detection)
options.cpc = 0.85; % Principal contribution rate (for ault detection)
% Train KPCA model
model = kpca_train(X,options);
figure
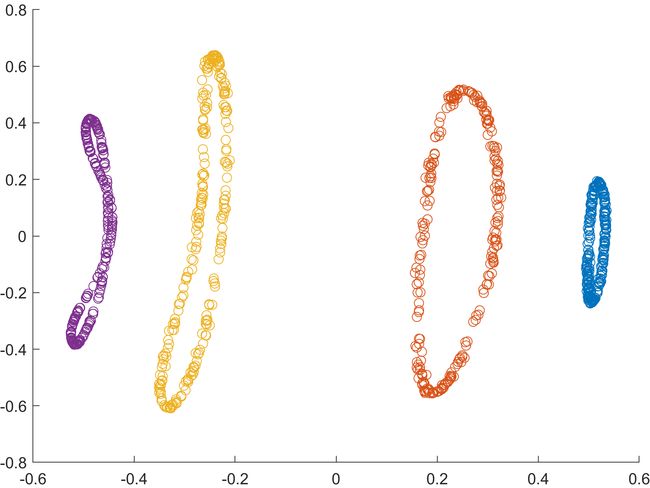
for i = 1:4
scatter(model.mappedX(1+250*(i-1):250*i,1), ...
model.mappedX(1+250*(i-1):250*i,2))
hold on
end
(2)结果 (分别为原图和特征提取后的图)
4. demo2: 故障检测(需要调节核宽度、主元贡献率和置信度等参数来提高故障检测效果)
(1)源代码
% Demo2: Fault detection
% X: training samples
% Y: test samples
% Improve the performance of fault detection by adjusting parameters
% 1. options.sigma = 16; % kernel width
% 2. options.beta % corresponding probabilities
% 3. options.cpc ; % principal contribution rate
% ---------------------------------------------------------------------%
clc
clear all
close all
addpath(genpath(pwd))
%
X = rand(200,10);
Y = rand(100,10);
Y(20:40,:) = rand(21,10)+3;
Y(60:80,:) = rand(21,10)*3;
% Normalization (if necessary)
% mu = mean(X);
% st = std(X);
% X = zscore(X);
% Y = bsxfun(@rdivide,bsxfun(@minus,Y,mu),st);
% Parameters setting
options.sigma = 16; % kernel width
options.dims = 2; % output dimension
options.type = 1; % 0:dimensionality reduction or feature extraction
% 1:fault detection
options.beta = 0.9; % corresponding probabilities (for ault detection)
options.cpc = 0.85; % principal contribution rate (for ault detection)
% Train KPCA model
model = kpca_train(X,options);
% Test a new sample Y (vector of matrix)
[SPE,T2,mappedY] = kpca_test(model,Y);
% Plot the result
plotResult(model.SPE_limit,SPE);
plotResult(model.T2_limit,T2);
(2)结果(分别是SPE统计量和T2统计量的结果图)
更新:
01 核函数
类 Kernel 用于计算核函数矩阵:
%{
type -
linear : k(x,y) = x'*y
polynomial : k(x,y) = (γ*x'*y+c)^d
gaussian : k(x,y) = exp(-γ*||x-y||^2)
sigmoid : k(x,y) = tanh(γ*x'*y+c)
laplacian : k(x,y) = exp(-γ*||x-y||)
degree - d
offset - c
gamma - γ
%}
kernel = Kernel('type', 'gaussian', 'gamma', value);
kernel = Kernel('type', 'polynomial', 'degree', value);
kernel = Kernel('type', 'linear');
kernel = Kernel('type', 'sigmoid', 'gamma', value);
kernel = Kernel('type', 'laplacian', 'gamma', value);例如,计算 X 和 Y 的高斯核函数矩阵:
X = rand(5, 2);
Y = rand(3, 2);
kernel = Kernel('type', 'gaussian', 'gamma', 2);
kernelMatrix = kernel.computeMatrix(X, Y);
>> kernelMatrix
kernelMatrix =
0.5684 0.5607 0.4007
0.4651 0.8383 0.5091
0.8392 0.7116 0.9834
0.4731 0.8816 0.8052
0.5034 0.9807 0.727402. 数据降维
以 helix 数据为例:
clc
clear all
close all
addpath(genpath(pwd))
load('.\data\helix.mat', 'data')
kernel = Kernel('type', 'gaussian', 'gamma', 2);
parameter = struct('numComponents', 2, ...
'kernelFunc', kernel);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(data);
% mapping data
mappingData = kpca.score;
% Visualization
kplot = KernelPCAVisualization();
% visulize the mapping data
kplot.score(kpca)训练结果为:
*** KPCA model training finished ***
running time = 0.2798 seconds
kernel function = gaussian
number of samples = 1000
number of features = 3
number of components = 2
number of T2 alarm = 135
number of SPE alarm = 0
accuracy of T2 = 86.5000%
accuracy of SPE = 100.0000%香蕉型数据的降维结果:
03. 数据重构
同心圆数据的重构结果:
clc
clear all
close all
addpath(genpath(pwd))
load('.\data\circle.mat', 'data')
kernel = Kernel('type', 'gaussian', 'gamma', 0.2);
parameter = struct('numComponents', 2, ...
'kernelFunc', kernel);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(data);
% reconstructed data
reconstructedData = kpca.newData;
% Visualization
kplot = KernelPCAVisualization();
kplot.reconstruction(kpca)04. 主元个数的确定
提供了两种方式来确定主元个数:主元贡献率和给定的数量
第一种:主元贡献率 (取值 0~1 之间)
通过键值对 'numComponents' - value 来设置。比如,将主元贡献率设置为 0.75:
clc
clear all
close all
addpath(genpath(pwd))
load('.\data\TE.mat', 'trainData')
kernel = Kernel('type', 'gaussian', 'gamma', 1/128^2);
parameter = struct('numComponents', 0.75, ...
'kernelFunc', kernel);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(trainData);
% Visualization
kplot = KernelPCAVisualization();
kplot.cumContribution(kpca)从上图可以看出,当主元个数为 21 的时候,主元贡献率为 75.2656%, 超过了给定的阈值(0.75)。
第二种:给定的数目
同样通过键值对 'numComponents' - value 来设置。比如,将主元个数设置为 24:
clc
clear all
close all
addpath(genpath(pwd))
load('.\data\TE.mat', 'trainData')
kernel = Kernel('type', 'gaussian', 'gamma', 1/128^2);
parameter = struct('numComponents', 24, ...
'kernelFunc', kernel);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(trainData);
% Visualization
kplot = KernelPCAVisualization();
kplot.cumContribution(kpca)从上图可以看出,当主元个数为 24 的时候,主元贡献率为 80.2539%。
05. 故障检测
数据来源于 TE 过程:
clc
clear all
close all
addpath(genpath(pwd))
load('.\data\TE.mat', 'trainData', 'testData')
kernel = Kernel('type', 'gaussian', 'gamma', 1/128^2);
parameter = struct('numComponents', 0.65, ...
'kernelFunc', kernel);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(trainData);
% test KPCA model
results = kpca.test(testData);
% Visualization
kplot = KernelPCAVisualization();
kplot.cumContribution(kpca)
kplot.trainResults(kpca)
kplot.testResults(kpca, results)训练的结果为
*** KPCA model training finished ***
running time = 0.0986 seconds
kernel function = gaussian
number of samples = 500
number of features = 52
number of components = 16
number of T2 alarm = 16
number of SPE alarm = 17
accuracy of T2 = 96.8000%
accuracy of SPE = 96.6000% 测试的结果为
*** KPCA model test finished ***
running time = 0.0312 seconds
number of test data = 960
number of T2 alarm = 799
number of SPE alarm = 851 06. 故障诊断
故障诊断通过键值对 'diganosis' - value 来进行设置。
比如对某个采样点(假设为500)出现的故障进行诊断,则: 'diagnosis', [500, 500]
比如对某个时间段(假设为300-500)出现的故障进行诊断,则: 'diagnosis', [300, 500]
具体代码为
clc
clear all
close all
addpath(genpath(pwd))
load('.\data\TE.mat', 'trainData', 'testData')
kernel = Kernel('type', 'gaussian', 'gamma', 1/128^2);
parameter = struct('numComponents', 0.65, ...
'kernelFunc', kernel,...
'diagnosis', [300, 500]);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(trainData);
% test KPCA model
results = kpca.test(testData);
% Visualization
kplot = KernelPCAVisualization();
kplot.cumContribution(kpca)
kplot.trainResults(kpca)
kplot.testResults(kpca, results)
kplot.diagnosis(results)故障诊断结果为
*** Fault diagnosis ***
Fault diagnosis start...
Fault diagnosis finished.
running time = 18.2738 seconds
start point = 300
ending point = 500
fault variables (T2) = 44 1 4
fault variables (SPE) = 1 44 18 可以看出,在300-500时间段,给出的故障变量参考为: 44,1(T2); 1,44(SPE)。