Batch Normalization与Layer Normalization的对比
文章目录
-
- 如何理解 Internal Covariate Shift(内部协变量漂移)?
-
- 白化的优缺点?
- Batch Normalization
-
- 请说明BN的原理,为什么要进行批归一化?
-
- 1. 原理
- 2. BN层的作用
-
- 2.1 加快网络的训练和收敛的速度
- 2.2 控制梯度爆炸防止梯度消失
- 2.3 防止过拟合
- 为什么BN层一般用在线性层和卷积层后面,而不是放在非线性单元后?
- Layer Normalization
- 对比BN和LN
- 为什么LN更适合于NLP?
如何理解 Internal Covariate Shift(内部协变量漂移)?
根本原因是神经网络每层之间,无法满足基本假设"独立同分布"。
在反向传播时,由于底层的参数随着训练更新,细微的变化通过层层叠加,也会导致顶层的输入分布发生巨大变化。
而机器学习中有个很重要的假设:IID独立同分布假设,就是假设训练数据和测试数据是满足相同分布的,这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。
那么,细化到神经网络的每一层间,每轮训练时分布都是不一致,那么相对的训练效果就得不到保障,所以称为层间的covariate shift。
解决方法:
- 白化
- PCA白化 - 均值为0,方差1
- ZCA白化 - 均值为0,方差相同
- Normalization
- Batch Normalization
- Layer Normalization
白化的优缺点?
优点:
-
- 使得输入特征分布具有相同的均值与方差;
-
- 去除了特征之间的相关性
缺点:
-
- 白化过程计算成本太高
-
- 白化过程由于改变了网络每一层的分布,因而改变了网络层中本身数据的表达能力,造成底层信息丢失
参考链接:Internal Covariate Shift(ICS)的理解 和 Batch Normalizaton的原理及优点
Batch Normalization
请说明BN的原理,为什么要进行批归一化?
1. 原理
在深度学习中,由于采用full batch的训练方式对内存要求较大,且每一轮训练时间过长;我们一般都会采用对数据做划分,用mini-batch对网络进行训练。因此,Batch Normalization也就在mini-batch的基础上进行计算。
按照传统白化的方法,整个数据集都会参与归一化的计算,但是这种过程无疑是非常耗时的。BN的归一化过程是以批量为单位的
BN一般置于每一层的激活层之前,通过如下公式,对数据进行规范化,保证数据变为均值为0、标准差为1的分布。这样使得激活输入值落在非线性函数对输入比较敏感的区域,网络的输出就不会很大,可以得到比较大的梯度,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
2. BN层的作用
BN层的作用主要有三个:
- 加快网络的训练和收敛的速度;
- 控制梯度爆炸防止梯度消失;
- 防止过拟合。
接下来就分析一下为什么BN层有着三个作用。
2.1 加快网络的训练和收敛的速度
在深度神经网络中中,如果每层的数据分布都不一样的话,将会导致网络非常难收敛和训练,而如果把 每层的数据都在转换在均值为零,方差为1 的状态下,这样每层数据的分布都是一样的训练会比较容易收敛。
2.2 控制梯度爆炸防止梯度消失
梯度消失:在深度神经网络中,如果网络的激活输出很大,其对应的梯度就会很小,导致网络的学习速率就会很慢,假设网络中每层的学习梯度都小于最大值0.25,网络中有n层,因为链式求导的原因,第一层的梯度将会小于0.25的n次方,所以学习速率相对来说会变的很慢,而对于网络的最后一层只需要对自身求导一次,梯度就大,学习速率就会比较快,这就会造成在一个很深的网络中,浅层基本不学习,权值变化小,而后面几层网络一直学习,后面的网络基本可以表征整个网络,这样失去了深度的意义。(使用BN层归一化后,网络的输出就不会很大,梯度就不会很小)
梯度爆炸:第一层偏移量的梯度=激活层斜率1x权值1x激活层斜率2x…激活层斜率(n-1)x权值(n-1)x激活层斜率n,假如激活层斜率均为最大值0.25,所有层的权值为100,这样梯度就会指数增加。使用bn层后权值的更新也不会很大。
2.3 防止过拟合
在网络的训练中,BN的使用使得一个minibatch中所有样本都被关联在了一起,因此网络不会从某一个训练样本中生成确定的结果,即同样一个样本的输出不再仅仅取决于样本的本身,也取决于跟这个样本同属一个batch的其他样本,而每次网络都是随机取batch,这样就会使得整个网络不会朝这一个方向使劲学习。一定程度上避免了过拟合。
为什么BN层一般用在线性层和卷积层后面,而不是放在非线性单元后?
原文中是这样解释的,因为非线性单元的输出分布形状会在训练过程中变化,归一化无法消除他的方差偏移,相反的,全连接和卷积层的输出一般是一个对称,非稀疏的一个分布,更加类似高斯分布,对他们进行归一化会产生更加稳定的分布。其实想想也是的,像relu这样的激活函数,如果你输入的数据是一个高斯分布,经过他变换出来的数据能是一个什么形状?小于0的被抑制了,也就是分布小于0的部分直接变成0了,这样不是很高斯了。
参考链接:神经网络中BN层的原理与作用
参考文献:Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Layer Normalization
LN来自Jimmy Lei Ba等人在2016年发表的论文Layer Normalization,为了解决BN的不足之处提出,相对BN的纵向标准化,LN可以称为横向标准化。
如上,LN根据单个样本计算该层的平均值及方差,之后用同一个再平移及缩放因子规范各位维度的输入,
如上,LN针对单个样本进行计算,避免了batch分布的影响,同时不需要保存每层的统计量,节省了存储空间。但是需要注意的是,相对BN标准化的是单一维度,LN是对所有维度同时进行标准化,假如各个维度表示的特征的纲量不一致(比如颜色和大小),那么会导致模型的表达能力下降。
对比BN和LN
Batch 顾名思义是对一个batch进行操作。假设我们有 10行 3列 的数据,即我们的batchsize = 10,每一行数据有三个特征,假设这三个特征是【身高、体重、年龄】。那么BN是针对每一列(特征)进行缩放,例如算出【身高】的均值与方差,再对身高这一列的10个数据进行缩放。体重和年龄同理。这是一种“列缩放”。
而layer方向相反,它针对的是每一行进行缩放。即只看一笔数据,算出这笔所有特征的均值与方差再缩放。这是一种“行缩放”。
细心的你已经看出来,layer normalization 对所有的特征进行缩放,这显得很没道理。我们算出一行这【身高、体重、年龄】三个特征的均值方差并对其进行缩放,事实上会因为特征的量纲不同而产生很大的影响。但是BN则没有这个影响,因为BN是对一列进行缩放,一列的量纲单位都是相同的。
那么我们为什么还要使用LN呢?因为NLP领域中,LN更为合适。
如果我们将一批文本组成一个batch,那么BN的操作方向是,对每句话的第一个词进行操作。但语言文本的复杂性是很高的,任何一个词都有可能放在初始位置,且词序可能并不影响我们对句子的理解。而BN是针对每个位置进行缩放,这不符合NLP的规律。
而LN则是针对一句话进行缩放的,且LN一般用在第三维度,如[batchsize, seq_len, dims]中的dims,一般为词向量的维度,或者是RNN的输出维度等等,这一维度各个特征的量纲应该相同。因此也不会遇到上面因为特征的量纲不同而导致的缩放问题。
如下图所示:
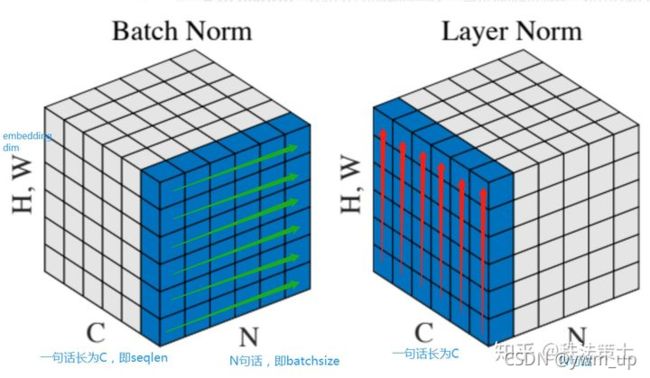
NLP中 batch normalization与 layer normalization
为什么LN更适合于NLP?
BN 感觉是对样本内部特征的缩放,LN 是样本直接之间所有特征的缩放。为啥BN不适合NLP,是因为NLP模型训练里的每次输入的句子都是多个句子,并且长度不一,那么,针对每一句的缩放才更加合理,才能表达每个句子之间代表不同的语义表示,这样让模型更加能捕捉句子之间的上下语义关系。如果要用BN,它首先要面临的长度不一的问题。有时候batch size 越小的BN效果更不好。


