【leetcode】接雨水问题
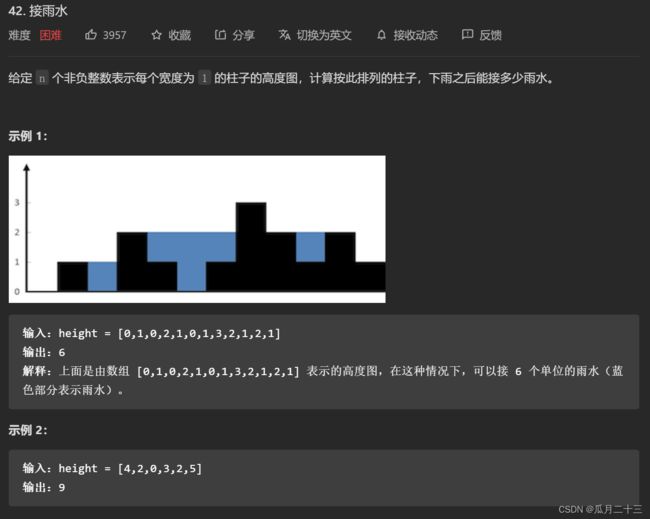
一、原题描述
二、解决方案
| 方法 | 时间复杂度 空间复杂度 |
|---|---|
| 暴力 | O(N^2) O(1) |
| 动态规划 | O(N) O(N) |
| 双指针 | O(N) O(1) |
| 单调栈 | O(N) O(N) |
三、方法详情
1、暴力 时间O(N^2) 空间O(1)
很明显每个柱子顶部可以储水的高度为:该柱子的左右两侧最大高度的较小者减去此柱子的高度。
因此我们只需要遍历每个柱子,累加每个柱子可以储水的高度即可。
此方法非常好理解,直接看下述代码中的注释即可。
class Solution {
public int trap(int[] height) {
int res = 0;
// 遍历每个柱子
for (int i = 1; i < height.length - 1; i++) {
int leftMax = 0, rightMax = 0;
// 计算当前柱子左侧的柱子中的最大高度
for (int j = 0; j <= i; j++) {
leftMax = Math.max(leftMax, height[j]);
}
// 计算当前柱子右侧的柱子中的最大高度
for (int j = i; j < height.length; j++) {
rightMax = Math.max(rightMax, height[j]);
}
// 结果中累加当前柱子顶部可以储水的高度,
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
res += (Math.min(leftMax, rightMax) - height[i]) > 0 ? Math.min(leftMax, rightMax) - height[i] : 0;
}
return res;
}
}
2、动态规划 时间O(N) 空间O(N)
在上述的暴力法中,对于每个柱子,我们都需要从两头重新遍历一遍求出左右两侧的最大高度,这里是有很多重复计算的,很明显最大高度是可以记忆化的,具体在这里可以用数组边递推边存储,也就是常说的动态规划DP。
具体做法:
- 定义二维dp数组 int[][] dp = new int[n][2]
- 其中,dp[i][0] 表示下标i的柱子左边的最大值
- dp[i][1] 表示下标i的柱子右边的最大值
- 分别从两头遍历height数组,为 dp[i][0]和 dp[i][1] 赋值
- 同方法1,遍历每个柱子,累加每个柱子可以储水的高度
源码:
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
// 定义二维dp数组
// dp[i][0] 表示下标i的柱子左边的最大值
// dp[i][1] 表示下标i的柱子右边的最大值
int[][] dp = new int[n][2];
dp[0][0] = height[0];
dp[n - 1][1] = height[n - 1];
for (int i = 1; i < n; i++) {
dp[i][0] = Math.max(height[i], dp[i - 1][0]);
}
for (int i = n - 2; i >= 0; i--) {
dp[i][1] = Math.max(height[i], dp[i + 1][1]);
}
// 遍历每个柱子,累加当前柱子顶部可以储水的高度,
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
int res = 0;
for (int i = 1; i < n - 1; i++) {
res += (Math.min(dp[i][0],dp[i][1]) - height[i]) > 0 ? Math.min(dp[i][0],dp[i][1]) - height[i] : 0;
}
return res;
}
}
3、双指针 时间O(N) 空间O(1)
在上述的动态规划方法中,我们用二维数组来存储每个柱子左右两侧的最大高度,但我们递推累加每个柱子的储水高度时其实只用到了 dp[i][0] 和 dp[i][1] 两个值,因此我们递推的时候只需要用 leftMax 和rightMax 两个变量就行了。
即将上述代码中的递推公式:
res += Math.min(dp[i][0], dp[i][1]) - height[i];
优化成:
res += Math.min(leftMax, rightMax) - height[i];
注意这里的 leftMax 是从左端开始递推得到的,而 rightMax 是从右端开始递推得到的。
因此遍历每个柱子,累加每个柱子的储水高度时,也需要用 left 和 right 两个指针从两端开始遍历。
class Solution {
public int trap(int[] height) {
int res = 0, leftMax = 0, rightMax = 0, left = 0, right = height.length - 1;
while (left <= right) {
if (leftMax <= rightMax) {
leftMax = Math.max(leftMax, height[left]);
res += leftMax - height[left++];
} else {
rightMax = Math.max(rightMax, height[right]);
res += rightMax - height[right--];
}
}
return res;
}
}
以上,就将空间复杂度从 O(N) 优化成了 O(1)。
4、单调栈 时间O(N) 空间O(N)
单调栈是本文想要重点说明的一个方法~
因为本题是一道典型的单调栈的应用题。
单调栈的处理逻辑:
先将下标0的柱子加入到栈中
stack.push(0)
然后开始从下标1开始遍历所有的柱子
for (int i = 1; i < height.size(); i++)
维护一个递减栈,如果当前遍历的元素(柱子)高度小于栈顶元素的高度,直接入栈;如果等于的话,那么要更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度;如果当前遍历的元素大于栈顶元素的高度,就出现凹槽了
先取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid]
此时的栈顶元素stack.peek(),就是凹槽的左边位置,下标为stack.peek(),对应的高度为height[stack.top()]
当前遍历的元素i,即,新插入的柱子,就是凹槽右边的位置,下标为i,对应的高度为height[i]
相当于就是栈顶和栈顶的下一个元素以及要入栈的三个元素来接水!
雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:
int h = min(height[stack.peek()], height[i]) - height[mid]
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:
int w = i - stack.top() - 1
通过上图可以发现,遍历到某些柱子的时候,会由于和之前的某个柱子形成凹槽,接住雨水。
这道题目可以用单调栈来做。单调栈就是比普通的栈多一个性质,即维护栈内元素单调。
比如当前某个单调递减的栈的元素从栈底到栈顶分别是:[10, 9, 8, 3, 2],如果要入栈元素5,需要把栈顶元素pop出去,直到满足单调递减为止,即先变成[10, 9, 8],再入栈5,就是[10, 9, 8, 5]。
代码就很简单了,具体见注释~
class Solution {
public int trap(int[] height) {
Stack<Integer> stack = new Stack<>();
int res = 0;
// 遍历每个柱体
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[stack.peek()] < height[i]) {
int mid = stack.pop();
// 如果栈顶元素一直相等,那么全都pop出去,只留第一个。
while (!stack.isEmpty() && height[stack.peek()] == height[mid]) {
stack.pop();
}
if (!stack.isEmpty()) {
// stack.peek()是此次接住的雨水的左边界的位置,右边界是当前的柱体,即i。
// Math.min(height[stack.peek()], height[i]) 是左右柱子高度的min,减去height[mid]就是雨水的高度。
// i - stack.peek() - 1 是雨水的宽度。
res += (Math.min(height[stack.peek()], height[i]) - height[mid]) * (i - stack.peek() - 1);
}
}
stack.push(i);
}
return res;
}
}