BLS综述

BLS从2017年被陈俊龙教授提出后，发展时间不长且未被广泛使用，参考 《Research Review for Broad Learning System: Algorithms, Theory, and Applications》这篇最新提出的综述，可以捋一捋宽度学习的目前发展

宽度学习基础

关于宽度学习的基础介绍，主要参考陈俊龙教授的《Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture》，关于这篇论文的学习我在之前的博客里略有笔记link

RBLS&GBLS

在《Novel Efficient RNN and LSTM-Like Architectures: Recurrent and Gated Broad Learning Systems and Their Applications for Text Classification》这篇论文中，提出了类似RNN和LSTM的宽度学习系统R-BLS，G-BLS

在NLP问题中，两个句子因素较为关键，一个是序列信息，另一个是 单词重要性。而对于宽度学习而言，因为mapped feature都是同等对待，因此体现不出这两个因素。

这里我们想到改进方式，将特征节点作为时序变化的节点，增强层将作用于X提取信息的重要程度。（注意这里增强层作用的是X而非Z）这也就是R-BLS的结构：

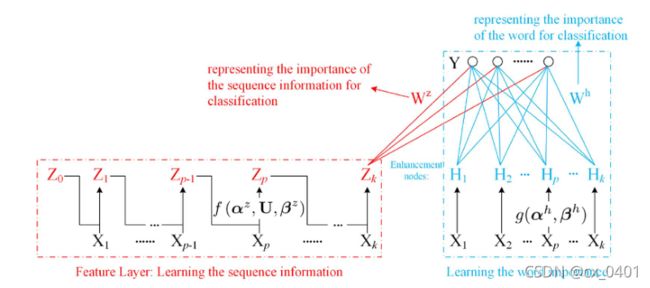
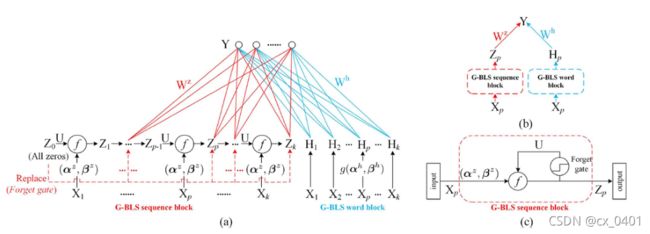
但我们观察这个结构发现，U作为原先RNN中训练的参数，这里作为了一个超参数。这也是我对这个结构优化性能持怀疑态度的地方

实际上，LSTM也就是在RNN的基础上增加了三个控制门，遗忘门、输入门、输出门，也就是在$Z_n$的迭代上不同

Convolutional BLS

有关BLS和CNN结合的工作较多，尚且还有些困惑

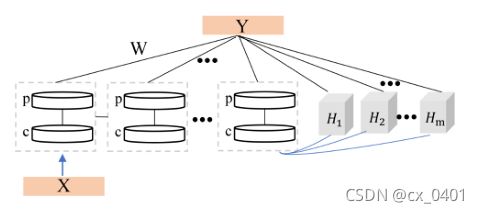
我们知道CNN实际上就是经过卷积、池化等操作的神经网络，可以用BLS中的mapped feature层来代替这个操作。

也比较类似于上文提到的R-BLS/G-BLS，实际上他们都属于一种层叠式的特征节点《Universal Approximation Capability of Broad
Learning System and Its Structural V ariations》，但这类节点间的参数都是随机确定的。

同时还有另一种BCNN的网络结构，参考《CNN-Based Broad Learning System》，在这篇论文中对于feature层使用Adam algorithm进行池化层和卷积层的参数优化。但是我没有很明白其中细节，这篇论文内容稍短只有5页。

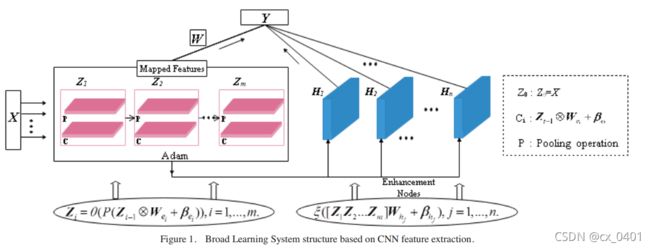
对于另外一篇《A CNN-Based Broad Learning System 》，在这篇论文中对于特征节点是用随机确定的卷积层和池化层来提取特征节点，增强层则是通过PCA方法获取。

实验部分是在手写字方面取得好的效果。

最后一篇关于CNN参考的论文是2020年发表的《Broad Convolutional Neural Network Based Industrial Process Fault Diagnosis With Incremental Learning Capability》，我还没有阅读到原文的内容，仅仅通过摘要和综述描写，判断它的结构应该是先建立一个普通的CNN，在这个基础上添加增强层，并可以通过增量学习逐步增加增强层节点来增强性能，将增强层的节点视为卷积和池化层。

对于这种结构我较为认可，因为这种条件下的增强层节点虽然是随机权值，但可以通过权值W控制是否采用或者变相提取信息。（！或许这也就是之前CNN卷积随机确认的证明）

Weighted BLS

参考《Weighted Broad Learning System and Its Application in Nonlinear Industrial Process Modeling》
在这篇论文中，主要是对输入的样本进行权值分配，努力排除一些噪声干扰。

这里设置一个新的变量$\theta$，初始化为单位矩阵。

最终的结束条件是$W_m$和$W_{m-1}$之间的差别在一定范围内。
那么这个问题的关键在于$\theta$的更新策略，文章使用了一些方法：
1）Huber Weight Function
2）Fair Weight Function
3）KED and PCA
（略，待填）

Fuzzy BLS

这里面涉及到一些模糊控制理论，这里主要是针对于大量高维数据，我们想通过一些模糊规则对数据进行降维处理，从而减少训练时间。文中提到的经典TS模糊系统，这里我们相当于在特征节点层用一些子模糊系统来代替之前的权值来进行特征提取。

Multiview BLS

《Multi-View Broad Learning System for Primate Oculomotor Decision Decoding》
这里引用的论文主要是将BLS应用在一个生物实验上，对于灵长类动物的眼球运动的决策。对于同一个数据源用不同的视图的数据，增强学习性能。

MvBLS结构

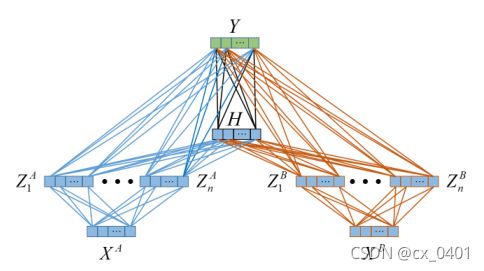
这里我们使用结构如上图：
输入两个视图数据$X^A$和$X^B$分别进行特征提取为$Z^A$和$Z^B$，然后共同建立增强层$H$，最后将$Z^A,Z^B,H$作为整体进行岭回归获取网络权值。

Manifold Learning

首先引用知乎上面一个非常形象化的定性解释：link

高维数据必然存在很多数据上的冗余，例如二维平面表示一个圆的时候，圆内部的空间是空的（冗余）。实际上我们只需要通过极坐标用半径就可以表示这个圆，这就是将二维数据表示成了一维数据。

另一个问题，例如三维空间内，地球。我们想得到上海到北京的距离，欧氏距离则是直接计算直线距离，而实际上我们需要的是将三维地球展开成平面后得到的距离。

流行学习关注的就是数据本身的流行结构，流形学习认为i我们观察到的数据实际上是由一个低维流形映射到高维空间上去的。所以针对上述的两个问题，我们通过流行学习对原始数据进行非线性+降维去冗余刻画事物的本质，并且能够得到更合理的“距离表示”。

比较常见的几种方法有
拉普拉斯特征映射 ，参考
这里应用了拉普拉斯矩阵$L=D-W$，目的是让之前保持近距离的数据仍然能保持近距离，具体的数学推导见链接。
…

在《Discriminative graph regularized broad learning system for image recognition》这篇论文中建立了一个新的GBLS，即在目标loss函数那里考虑到数据在变化维度时的一致性。

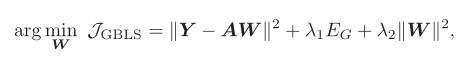
文中主要考虑了$E_G$的规划问题，并以此提出了新的权值公式

Ensemble Learning

关于集成学习，其实就是三个臭皮匠顶一个诸葛亮的故事，训练多个子系统综合考虑，这里不再赘述。