二叉树的遍历

二叉树的遍历方式

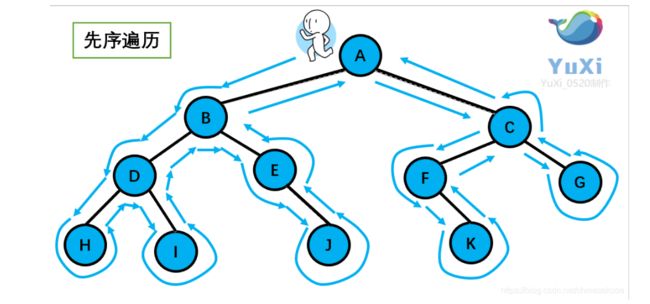
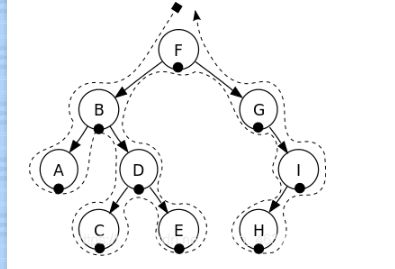
先序遍历

先序遍历指遍历顺序为根节点——》左节点——》右节点

代码实现：

	//存储遍历结果的数组
	vector v;
	//前序遍历函数
    vector preorderTraversal(TreeNode* root) {
        if(root==nullptr) return v;
        v.emplace_back(root->val); //输入数组语句
        preorderTraversal(root->left);
        preorderTraversal(root->right);
        return v;
    }

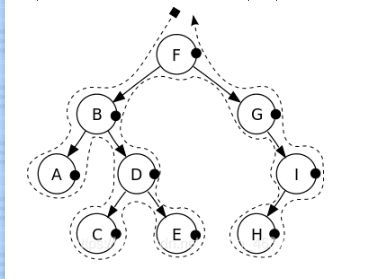
中序遍历

中序遍历指遍历顺序为左节点——》根节点——》右节点

	//存储遍历结果的数组
	vector v;
	//前序遍历函数
    vector preorderTraversal(TreeNode* root) {
        if(root==nullptr) return v;
        preorderTraversal(root->left);
         v.emplace_back(root->val); //输入数组语句
        preorderTraversal(root->right);
        return v;
    }

后序遍历

后序遍历指遍历顺序为左节点——》右节点——》根节点

	//存储遍历结果的数组
	vector v;
	//前序遍历函数
    vector preorderTraversal(TreeNode* root) {
        if(root==nullptr) return v;
        preorderTraversal(root->left);
        preorderTraversal(root->right);
        v.emplace_back(root->val); //输入数组语句
        return v;
    }

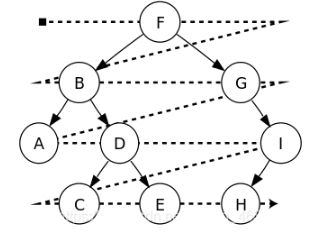
层序遍历

层序遍历指按各节点到根节点的最短距离（层数）来遍历

   vector> levelOrder(TreeNode* root) {
     vector> v;
     if(root == NULL) return v;  //特判
     queue q;  //队列
     TreeNode* temp = NULL;
     q.push(root);
     while(!q.empty()) //队列为空跳出循环
     {
         vector ans; //存放每一层的数字
         int n = q.size(); //每一层的个数
         for (int i=0;ival);
             if(temp->left != NULL) q.push(temp->left);
             if(temp->right != NULL) q.push(temp->right);
         }
         v.emplace_back(ans);
     }
     return v;
 }

类似bfs的过程

根据遍历过程构造二叉树

先序遍历的特点：第一个肯定是根节点

后序遍历的特点：最后一个肯定是根节点

中序遍历的特点：根节点的左侧都是左子树的节点，右侧都是右子树的节点

结合以上特点，我们可知根据先中遍历可以确定一颗二叉树，根据中后遍历也可以确定一颗二叉树。但是先后遍历因为无法确定根节点，所以无法确定二叉树。

根据先序和中序遍历建树

struct T{
	int l, r;
}a[N];

int build(int pl, int pr, int il, int ir)
{
	int root = pre[pl]; //root为先序中的第一个元素
	int k = mp[root]; //k为该子树根节点root在中序数列中的位置 
	if(k > il) a[root].l = build(pl+1, k-il+pl, il, k-1); 
	//k>il,中序数列中，根节点左边有位置，则说明有左子树，就更新 
	if(k < ir) a[root].r = build(k-il+pl+1, pr, k+1, ir);
	
	return root; //父节点的左孩子是左子树的根节点（或右孩子是右子树的根节点），故返回根节点 
}
int main(){
	cin >> n;
	for(int i=1;i<=n;i++) cin >> pre[i];
	for(int i=1;i<=n;i++){
		cin >> post[i];
		mp[post[i]] = i; //记录每个点在中序数列中的位置 
	}
	build(1, n, 1, n); //最大的树
	return 0;
}

build函数中的参数怎么记？

可以这样想象，前两个参数指的是在先序遍历中当前子树的范围l,r.后两个参数指的是在中序遍历中当前子树的范围L,R。

所以对于当前树来说，知道根节点在中序遍历的位置k

左子树的先序遍历范围l=l+1,r=k-L+l

左子树的中序遍历范围L=L,R=k-1

右子树的先序遍历范围l=k-L+l+1,r=r

右子树的中序遍历范围L=k+1,R=R

根据中序和后序遍历建树

struct T{
	int l, r;
}a[N];

int  build(int il, int ir, int pl, int pr)
{ 
	int root = post[pr];//该段后序中的最后一个元素就是该子树的根 
	int k = mp[root]; //找出此根在中序中的位置k 
	if(il < k) a[root].l = build(il, k-1, pl, k+pl-il-1); //k前面有数，说明有左子树，则其左节点为前面一段中，后序的最后一个（递归到下一段） 
	if(ir > k) a[root].r = build(k+1, ir, k+pl-il, pr-1);
	return root; //该树的根 
}
int main(){
	cin >> n;
	for(int i=1;i<=n;i++) cin >> post[i];
	for(int j=1;j<=n;j++) cin >> in[j], mp[in[j]] = j;
	
	build(1, n, 1, n);
	return 0;
} 

同理

所以对于当前树来说，知道根节点在中序遍历的位置k

左子树的后序遍历范围l=l,r=k-L+l-1

左子树的中序遍历范围L=L,R=k-1

右子树的后序遍历范围l=k-L+l,r=r-1

右子树的中序遍历范围L=k+1,R=R

已知前序(后序)中序输出后序(前序)

可以先构造树再按后序遍历的方法跑一边。

也可以直接将构造树的过程看做遍历，在构造树的时候就直接输出后序遍历。

为什么可以直接输出？

因为构造树的时候，我们每次找的是根节点，再找左右节点。

在遍历的时候也是每次从根节点下手开始递归。

关键就是你输出语句放的位置，会直接影响到你输出的是后序遍历还是先序遍历。

struct node{
    int l,r;
} tr[100];
int build(int l,int r,int L,int R)
{
	int root=back[r-1];
	int k=ma[root];
	if(k>L) tr[root].l=build(l,k-L+l-1,L,k-1);
	if(k

struct node{
    int l,r;
} tr[100];
int build(int l,int r,int L,int R)
{
	int root=back[r-1];
	int k=ma[root];
	cout<L) tr[root].l=build(l+1,k-L+l,L,k-1);
	if(k