线索二叉树的基本概念、构造过程、遍历过程详解及C++代码详细实现
线索二叉树
前置知识点如下:
树与二叉树的定义,性质。二叉树的顺序存储结构,链式存储结构。
二叉树的先序,中序,后序,层序遍历;由遍历序列构造二叉树详解及C++详细实现
1.线索二叉树的基本概念
遍历二叉树是以一定的规则将二叉树中的结点排列成一个线性序列,从而得到几种遍历序列,使得该序列中的每个结点(第一个和最后一个结点除外)都有一个直接前驱和直接后继。
传统的二叉链表存储仅能体现一种父子关系,不能直接得到结点在遍历中的前驱或后继。前面提到,在含 n {\rm n} n 个结点的二叉树中,有 n + 1 {\rm n+1} n+1 个空指针。这是因为每个叶结点有2个空指针,每个度为1的结点有1个空指针,空指针总数为 2 n 0 + n 1 {\rm 2n_0+n_1} 2n0+n1 ,又 n 0 = n 2 + 1 {\rm n_0=n_2+1} n0=n2+1,所以空指针总数为 n 0 + n 1 + n 2 + 1 = n + 1 {\rm n_0+n_1+n_2+1=n+1} n0+n1+n2+1=n+1。由此设想能否利用这些空指针来存放指向其前驱或后继的指针?这样就可以像遍历单链表那样方便地遍历二叉树。引入线索二叉树正是为了加快查找结点前驱和后继的速度。
规定:若无左子树,令lchild指向其前驱结点;若无右子树,令rchild指向其后继结点。 如下图所示,还需增加两个标志域标识指针域是指向左(右)孩子还是指向前驱(后继)。

其中,标志域的含义如下:

线索二叉树的存储结构描述如下:
template<typename T>
struct ThreadNode {
T data;
ThreadNode *lchild, *rchild; //左右孩子指针
int ltag, rtag; //左右线索标志
};
以这种结点结构构成的二叉链表作为二叉树的存储结构,称为线索链表,其中指向结点前驱和后继的指针称为线索。加上线索的二叉树称为线索二叉树。
2.中序线索二叉树的构造
二叉树的线索化是将二叉链表中的空指针改为指向前驱或后继的线索。而前驱或后继的信息只有在遍历时才能得到,因此线索化的实质就是遍历一次二叉树。
以中序线索二叉树的建立为例。附设指针 p r e {\rm pre} pre 指向刚刚访问过的结点,指针 p {\rm p} p 指向正在访问的结点,即 p r e {\rm pre} pre 指向 p {\rm p} p 的前驱。在中序遍历的过程中,检查 p {\rm p} p 的左指针是否为空,若为空就将它指向 p r e {\rm pre} pre ;检查 p r e {\rm pre} pre 的右指针是否为空,若为空就将它指向 p {\rm p} p ,如下图所示。

通过中序遍历对二叉树线索化的递归算法如下:
#include 为了方便,可以在二叉树的线索链表上也添加一个头结点,令其lchild域的指针指向二叉树的根结点,其rchild域的指针指向中序遍历时访问的最后一个结点;令二叉树中序序列中的第一个结点的lchild域指针和最后一个结点的rchild域指针均指向头结点。这好比为二叉树建立了一个双向线索链表,方便从前往后或从后往前对线索二叉树进行遍历,如下图所示。
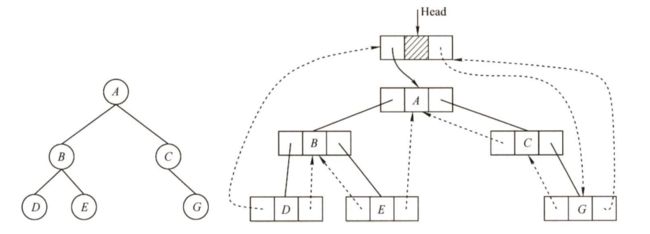
3.中序线索二叉树的遍历
中序线索二叉树的结点中隐含了线索二叉树的前驱和后继信息。在对其进行遍历时,只要先找到序列中的第一个结点,然后依次找结点的后继,直至其后继为空。在中序线索二叉树中找结点后继的规律是:若其右标志为"1”,则右链为线索,指示其后继,否则遍历右子树中第一个访问的结点(右子树中最左下的结点)为其后继。不含头结点的线索二叉树的遍历算法如下
template<typename T>
class ThreadTree {
private:
ThreadNode<T> *root;
//中序线索二叉树的遍历
ThreadNode<T> *FirstNode(ThreadNode<T> *p) {
while (p->ltag == 0)
p = p->lchild;//找到以p为根节点的子树的最左下结点(不一定是叶子结点)
return p;
}
ThreadNode<T> *InNextNode(ThreadNode<T> *p) {
if (p->rtag == 0) //当前结点右子树不为空,后继结点为右子树最左边的结点
return FirstNode(p->rchild);
else
return p->rchild; //当前结点右子树为空,右孩子存放的是后继线索
}
public:
//中序线索二叉树的中序遍历算法
void InOrderThread() {
cout << "InOrder:" << "\t";
if (root) {
//找到中序遍历序列的第一个结点,即整个二叉树的最左下的结点
ThreadNode<T> *p = FirstNode(root);
while (p) {
cout << p->data << "\t";
p = InNextNode(p);//寻找结点p的后继结点
}
}
}
};
中序线索二叉树的构造与遍历全部代码以及测试代码如下:
二叉树构造算法详解点击此处
输入:ABD##E##C#G##
#include 运行结果:
ABD##E##C#G## //输入
InOrder: D B E A C G
4.先序线索二叉树和后序线索二叉树
上面给出了建立中序线索二叉树的代码,建立先序线索二叉树和后序线索二叉树的代码类似,只需变动线索化改造的代码段与调用线索化左右子树递归函数的位置。

先序线索二叉树的构造
以图(a)所示的二叉树为例,给出手动求先序线索二叉树的过程:先序序列为 A B C D F {\rm ABCDF} ABCDF ,然后依次判断每个结点的左右链域,如果为空则将其改造为线索。
结点 A , B {\rm A,B} A,B 均有左右孩子;
结点 C {\rm C} C 无左孩子,将左链域指向前驱 B {\rm B} B ,无右孩子,将右链域指向后继 D {\rm D} D ;
结点 D {\rm D} D 无左孩子,将左链域指向前驱 C {\rm C} C ,无右孩子,将右链域指向后继 F {\rm F} F ;
结点 F {\rm F} F 无左孩子,将左链域指向前驱 D {\rm D} D ,无右孩子,也无后继故置空。
得到的先序线索二叉树如图(b)所示。
通过先序遍历对二叉树线索化的递归算法如下:
template<typename T>
class ThreadTree {
private:
//通过先序遍历线索化二叉树
void PreThread(ThreadNode<T> *p) {
if (p) {
if (p->lchild == NULL) { //左子树为空,建立前驱线索
p->lchild = pre;
p->ltag = 1;
}
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = p; //建立前驱结点的后继线索
pre->rtag = 1;
}
pre = p; //标记当前结点成为刚刚访问过的结点
if (p->ltag == 0) //保证左孩子存放的不是线索,才能继续递归遍历
PreThread(p->lchild);//递归,线索化左子树
if (p->rtag == 0) //保证右孩子存放的不是线索,才能继续递归遍历
PreThread(p->rchild);//递归,线索化右子树
}
}
public:
//通过先序遍历线索化二叉树
void CreatePreThread() {
pre = NULL;
PreThread(root); //线索化二叉树
pre->rchild = NULL; //处理遍历的最后一个结点
pre->rtag = 1;
}
};
先序线索二叉树的遍历
如何在先序线索二叉树中找结点的后继?
如果有左孩子,则左孩子就是其后继;
如果无左孩子但有右孩子,则右孩子就是其后继;
如果为叶结点,则右链域直接指示了结点的后继。
template<typename T>
class ThreadTree {
private:
//先序线索二叉树的遍历
ThreadNode<T> *PreNextNode(ThreadNode<T> *p) {
if (p->ltag == 0) //如果有左孩子,则左孩子就是其后继;
return p->lchild;
else if (p->ltag == 1 && p->rtag == 0) //如果无左孩子但有右孩子,则右孩子就是其后继;
return p->rchild;
else //如果为叶结点,则右链域直接指示了结点的后继。
return p->rchild;
}
public:
//先序线索二叉树的先序遍历算法
void PreOrderThread() {
cout << "PreOrder" << "\t";
if (root) {
//先序遍历的第一个结点就是根结点
ThreadNode<T> *p = root;
while (p) {
cout << p->data << "\t";
p = PreNextNode(p);
}
}
}
};
先序线索二叉树的构造与遍历全部代码以及测试代码如下:
二叉树构造算法详解点击此处
输入:ABC##D##F##
#include 运行结果:
ABC##D##F## //输入
PreOrder A B C D F
后序线索二叉树的构造
求后序线索二叉树的过程:
后序序列为 C D B F A {\rm CDBFA} CDBFA ,
结点 C {\rm C} C 无左孩子,也无前驱故置空,无右孩子,将右链域指向后继 D {\rm D} D ;
结点 D {\rm D} D 无左孩子,将左链域指向前驱 C {\rm C} C ,无右孩子,将右链域指向后继 B {\rm B} B ;
结点 F {\rm F} F 无左孩子,将左链域指向前驱 B {\rm B} B ,无右孩子,将右链域指向后继 A {\rm A} A 。
得到的后序线索二叉树如图©所示
后序线索二叉树的遍历
在后序线索二叉树中找结点的后继较为复杂,可分3种情况:
1)若结点 x {\rm x} x 是二叉树的根,则其后继为空;
2)若结点 x {\rm x} x 是其双亲的右孩子,或是其双亲的左孩子且其双亲没有右子树,则其后继即为双亲;
3)若结点 x {\rm x} x 是其双亲的左孩子,且其双亲有右子树,则其后继为双亲的右子树上按后序遍历列岀的第一个结点;
图©中找结点 B {\rm B} B 的后继无法通过链域找到,可见在后序线索二叉树上找后继时需知道结点双亲,即需采用带标志域的三叉链表作为存储结构。(有兴趣的下来自己实现,这里不再赘述)