[入门必看]数据结构4.2:串的模式匹配
[入门必看]数据结构4.2:串的模式匹配
- 第四章 串
- 4.2 串的模式匹配
-
- 知识总览
-
- 4.2.1_朴素模式匹配算法
- 4.2.2_1_KMP算法
- 4.2.2_2_求next数组
- 4.2.3_KMP算法的进一步优化
- 4.2.1_朴素模式匹配算法
-
- 什么是字符串的模式匹配
- 朴素模式匹配算法
- 通过数组下标实现朴素模式匹配算法
-
- 代码实现:
- 4.2.2_1_KMP算法
-
- 优化思路 - 模式串的最后一个位置不匹配
- 优化思路 - 其他位置不匹配
- 上节例子对比
- 对例子进行改造
- KMP算法
-
- 利用next数组进行匹配
- 朴素模式匹配 v.s. KMP算法
- 4.2.2_2_求next数组
-
- 练习1:
-
- 手算next数组
- 使⽤next数组进⾏模式匹配
- 练习2:
- 练习3:
- 4.2.3_KMP算法的进一步优化
-
- 例1:第三个位置失配
- 例2:第五个位置失配
- 练习1:
- 练习2:
- 优化KMP算法
-
- 优化前:
- 优化后:
- 知识回顾与重要考点
-
- 4.2.1_朴素模式匹配算法
- 4.2.2_1_KMP算法
- 4.2.2_2_求next数组
- 4.2.3_KMP算法的进一步优化
第四章 串
小题考频:2
大题考频:0
4.2 串的模式匹配
难度:☆☆☆☆☆
知识总览
4.2.1_朴素模式匹配算法
4.2.2_1_KMP算法
4.2.2_2_求next数组
4.2.3_KMP算法的进一步优化
4.2.1_朴素模式匹配算法
什么是字符串的模式匹配
查找功能
搜索引擎
- 字符串模式匹配:在主串中找到与模式串相同的⼦串,并返回其所在位置。
子串——主串的一部分,一定存在
模式串——不一定在主串中找到
朴素模式匹配算法
——暴力解决问题
在主串中找出所有有可能与模式串相匹配的子串,并将这些子串和模式串一一进行对比
![[入门必看]数据结构4.2:串的模式匹配_第5张图片](http://img.e-com-net.com/image/info8/8e564bf6a36b4d65b8b9a335ecfab5c2.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第6张图片](http://img.e-com-net.com/image/info8/ad7efd2e2f794d238c79729f66e171df.jpg)
朴素模式匹配算法:将主串中所有长度为m的子串依次与模式串对比,直到找到一个完全匹配的子串,或所有的子串都不匹配为止。
最多对比 n - m + 1 个子串
上一节中Index(S,T)函数的实现,采用的就是朴素模式匹配算法的思想。
1)int i=1 - 指明当前要匹配的子串是从哪个位置开始的;
2)(i<=n-m+1) - 表示最多对比n-m+1个子串;
3)SubString(sub,S,i,m); - 从主串S中,取出从位置i开始,长度为m的子串,放到sub里;
4)if(StrCompare(sub,T)!=0) ++i; - 子串和模式串对比,若不匹配,则匹配下一个子串
5)若能匹配,返回当前子串的起始位置i;
6)若都不能匹配,返回0
上述代码使用了:1)取子串的基本操作;2)对比两个字符串的基本操作
接下来:不使用字符串的基本操作,直接通过数组下标实现朴素模式匹配算法。
通过数组下标实现朴素模式匹配算法
设置两个扫描指针i和j,这两个指针指到哪就要把字符对比到哪。
Step1:
开始匹配第1个子串
对比主串和模式串的第1个字符
![[入门必看]数据结构4.2:串的模式匹配_第17张图片](http://img.e-com-net.com/image/info8/6fb0f38717874826bc9bcc2d62af08af.jpg)
Step2:
如果指向的字符相等,那么让指针i和j分别后移
![[入门必看]数据结构4.2:串的模式匹配_第18张图片](http://img.e-com-net.com/image/info8/adaf1e168bd94813a8dda1253228f306.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第19张图片](http://img.e-com-net.com/image/info8/d4a85440b2df46fe80ec104a32d12d8a.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第20张图片](http://img.e-com-net.com/image/info8/bc78dbfffedb4713877bc6172d4e4eb9.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第21张图片](http://img.e-com-net.com/image/info8/45b640aadc6947a89bbdaa888a2b4f03.jpg)
Step3:
到了第6个位置时,i和j所指向的字符不相等,则认为第一个子串匹配失败。
![[入门必看]数据结构4.2:串的模式匹配_第22张图片](http://img.e-com-net.com/image/info8/68774d93196c4a49abb1510517a44e85.jpg)
若当前⼦串匹配失败,则主串指针 i 指向下⼀个⼦串的第⼀个位置,模式串指针 j 回到模式串的第⼀个位置
i = i - j + 2
(i - j:指针指向当前子串的前一个位置;+2:指向下一个子串的起始位置)
j = 1
Step4:
第1个子串匹配失败后:
i的值回到2
j的值回到1
然后开始匹配第2个子串
![[入门必看]数据结构4.2:串的模式匹配_第23张图片](http://img.e-com-net.com/image/info8/6b04c8ea80244675850877b1768cfdde.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第24张图片](http://img.e-com-net.com/image/info8/57875ebc805649a1838802f6c5c7270e.jpg)
匹配失败,则主串指针 i 指向下⼀个⼦串的第⼀个位置,模式串指针 j 回到模式串的第⼀个位置
Step4:
匹配下一个子串
![[入门必看]数据结构4.2:串的模式匹配_第25张图片](http://img.e-com-net.com/image/info8/abccf35a0284451b8772a849bc363fb5.jpg)
失败,i 指向下一个子串的第一个位置,j 指向模式串第一个位置,开始匹配下一个子串。
Step5:
匹配成功!
![[入门必看]数据结构4.2:串的模式匹配_第26张图片](http://img.e-com-net.com/image/info8/96a80afeadcb4247bb356c0282fef902.jpg)
若 j 指针大于模式串长度,j > T.length(模式串字符全部匹配成功),则当前⼦串匹配成功,返回当前⼦串第⼀个字符的位置 —— i - T.length
代码实现:
![[入门必看]数据结构4.2:串的模式匹配_第27张图片](http://img.e-com-net.com/image/info8/7bb57a692fb84937b0fa4ae9c1e27d8e.jpg)
设主串⻓度为 n,模式串⻓度为 m,则
最坏时间复杂度 = O(nm)
![[入门必看]数据结构4.2:串的模式匹配_第28张图片](http://img.e-com-net.com/image/info8/3ee531cdbe5c4987a83d4d80f7f5fc96.jpg)
最坏的情况,每个⼦串都要对⽐ m 个字符,共 n-m+1 个⼦串,复杂度 = O((n-m+1)m) = O ( n m ) O(nm) O(nm)
注:很多时候,n >> m,
保留数量级更大的项,把 O ( n m − m 2 + m ) O(nm-m^2+m) O(nm−m2+m)简化为 O ( n m ) O(nm) O(nm)
4.2.2_1_KMP算法
——由D.E.Knuth,J.H.Morris和V.R.Pratt提出,因此称为KMP算法
对于朴素模式匹配算法,⼀旦发现当前这个⼦串中某个字符不匹配,就只能转⽽匹配下⼀个⼦串(从头开始)
![[入门必看]数据结构4.2:串的模式匹配_第29张图片](http://img.e-com-net.com/image/info8/f1da09e20cb642c8b41c9583f8212063.jpg)
因为我们并不知道主串里面这些字符到底是什么,所以我们必须从子串开头的第一个字符开始匹配。
如果匹配模式串时,在最后一个字符匹配失败,那么主串中之前这些字符就和模式串中的字符对应。
那么在主串中匹配失败的位置,的之前的字符,是已知的,和模式串时保持一致的。
![[入门必看]数据结构4.2:串的模式匹配_第30张图片](http://img.e-com-net.com/image/info8/3182fde57ac04cde9667e2d658ed3d3d.jpg)
不匹配的字符之前,一定是和模式串一致的
在朴素模式匹配算法中,匹配失败后只能从第2个子串开始重新匹配:
![[入门必看]数据结构4.2:串的模式匹配_第31张图片](http://img.e-com-net.com/image/info8/2ee19f61150941bab118041d02c27a97.jpg)
但是匹配第2个子串时,已知了主串中的前面这几个字符,发现刚开始就已经不匹配了,所以根本没有必要去检查和匹配。
![[入门必看]数据结构4.2:串的模式匹配_第32张图片](http://img.e-com-net.com/image/info8/96bf377ae0054a28a3d25ed2224474f0.jpg)
第3个子串一样,已经知道了主串前面的几个字符,对不上,也没有必要去检查和匹配了。
![[入门必看]数据结构4.2:串的模式匹配_第33张图片](http://img.e-com-net.com/image/info8/1d7e8516dc084ce1af2574dbb74987cd.jpg)
匹配第4个子串时,主串里已知部分和模式串是能够匹配的,其他部分能否匹配现在还不知道,那么在这个子串中,可以从未知部分往后进行检查和匹配:
![[入门必看]数据结构4.2:串的模式匹配_第34张图片](http://img.e-com-net.com/image/info8/48cc5d2eb0d94cdead2fb2a8c06a1f8d.jpg)
优化思路 - 模式串的最后一个位置不匹配
![[入门必看]数据结构4.2:串的模式匹配_第35张图片](http://img.e-com-net.com/image/info8/86059c9ddd1e402088b1f6e40cb647c2.jpg)
①不匹配的字符之前,一定是和模式串一致的;
②所以没有必要检查已知部分和模式串不匹配的子串;
③已知部分和模式串相匹配的子串中,已经匹配的部分(已知部分)也不用再次对比;
④直接从【已知部分和模式串相匹配的子串】的未知部分开始匹配。
![[入门必看]数据结构4.2:串的模式匹配_第36张图片](http://img.e-com-net.com/image/info8/c5fa6b79756b4970931c9075df9dff87.jpg)
跳过了中间几个子串的对比,也调过了当前子串已知的部分的对比,提高了算法效率
对于模式串 T = ‘abaabc’,当第6个元素匹配失败时,可令主串指针 i 不变(指向当前失配的字符),模式串指针 j=3(从模式串的第3个字符向后依次匹配)
得到的结论只和模式串有关,与匹配到主串的哪个位置没有关系。
验证(从第5个位置开始匹配):
![[入门必看]数据结构4.2:串的模式匹配_第37张图片](http://img.e-com-net.com/image/info8/db8413b8ca2b4056bc8a59948a2fe64b.jpg)
匹配到当前子串的最后一个字符时,字符失配。
那么前面的字符就和模式串保持一致,即已知部分。
![[入门必看]数据结构4.2:串的模式匹配_第38张图片](http://img.e-com-net.com/image/info8/05edf44326ed4d6a9f0884a222d45eb8.jpg)
使用之前的结论:
对于模式串 T = ‘abaabc’,当第6个元素匹配失败时,可令主串指针 i 不变(指向当前失配的字符),模式串指针 j=3(从模式串的第3个字符向后依次匹配)
![[入门必看]数据结构4.2:串的模式匹配_第39张图片](http://img.e-com-net.com/image/info8/9ae65789468347f3a028e70077d4e8d7.jpg)
验证了该结论对模式串’abaabc’具有通⽤性,和主串没有半⽑钱关系。
以上是对于模式串T = ’abaabc’的第6个元素匹配失败的情况。
优化思路 - 其他位置不匹配
考虑其他位置的情况。
对于模式串 T = ‘abaabc’,当第5个元素匹配失败时? 怎么搞?
- 第5个元素匹配失败,可以知道主串中前面4个元素的信息,与模式串保持一致
此时可令主串指针i不变,模式串指针j = 2
从模式串的第二个元素开始匹配即可
- 第4个元素匹配失败,可以知道主串中前面3个元素的信息,与模式串保持一致
此时可令主串指针i不变,模式串指针j = 2
从模式串的第二个元素开始匹配即可
- 第3个元素匹配失败,可以知道主串中前面2个元素的信息,与模式串保持一致
此时可令主串指针i不变,模式串指针j = 1
从模式串的第一个元素开始匹配即可
- 第2个元素匹配失败,可以知道主串中前面1个元素的信息,与模式串保持一致
此时可令主串指针i不变,模式串指针j = 1
从模式串的第一个元素开始匹配即可
结论:
对于模式串 T = ‘abaabc’
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
上节例子对比
朴素模式匹配算法,此时应令i = i - j + 3,j = 1;
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
优化之后,主串指针不需要回溯。
采用这种策略,效率大幅度提高。
对例子进行改造
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当#pic_center第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
最终因为指针j超出模式串的范围而停止:
![[入门必看]数据结构4.2:串的模式匹配_第69张图片](http://img.e-com-net.com/image/info8/ed4ce5e3f55d4b3e87076f5f847706e1.jpg)
完成匹配工作。
整个过程中i不用回溯。
怎么⽤代码实现这个处理逻辑?
对于模式串T = ‘abaabc’
用数组来表示模式串指针需要修改的信息
![[入门必看]数据结构4.2:串的模式匹配_第70张图片](http://img.e-com-net.com/image/info8/c91ddccd590e428f98b4b9c9df285bd8.jpg)
特别地,第1个元素失配时,要将j = 0 再让 i++, j++
if (S[i] != T[j]) //模式串在第几个位置失配时,使用第几个位置的指针修改信息
j = next[j];
if(j == 0) {i++; j++} //第1个位置时,匹配下一个相邻子串
KMP算法
是的,这就是KMP算法。
![[入门必看]数据结构4.2:串的模式匹配_第71张图片](http://img.e-com-net.com/image/info8/75d8b118805e4062904a6c32c11360b1.jpg)
KMP算法的整体流程就是在进行模式匹配之前,需要先进行一个预处理:
- 分析模式串,求出和模式串相对应的这个next数组。
- 然后再利用next数组来进行模式匹配,整个匹配的过程主串的指针i是不需要回溯的。
利用next数组进行匹配
传入主串的值S、模式串的值T、和模式串相对应的这个next数组;
从主串的1和模式串的1位置开始往后匹配;
如果,主串的当前元素和模式串的当前元素相等的话,即匹配成功,i和j同时++;
并且当j == 0时,也需要让i和j同时++
否则,说明i和j所指元素不匹配,失配时让j = next[j]即可。
朴素模式匹配 v.s. KMP算法
![[入门必看]数据结构4.2:串的模式匹配_第73张图片](http://img.e-com-net.com/image/info8/2f8cd113a6fb4964bf8f2bc30785e31b.jpg)
对比发现,其实修改的部分即黄色框所框出部分,和需要传入一个next数组。
有了next数组后,当主串和模式串发生失配时,不需要再修改主串的指针i让其回溯,只需要修改模式串的j指针即可。
朴素模式匹配算法,最坏的时间复杂度 O ( m n ) O(mn) O(mn)
KMP算法,最坏的时间复杂度 O ( m + n ) O(m+n) O(m+n)
其中,求 next 数组时间复杂度 O(m)
模式匹配过程最坏时间复杂度 O(n)
需要掌握手算next数组的方法。
4.2.2_2_求next数组
——(⼿算练习)
next数组的作⽤:当模式串的第 j 个字符失配时,从模式串的第 next[j] 继续往后匹配
练习1:
手算next数组
 的next数组:
的next数组:
![[入门必看]数据结构4.2:串的模式匹配_第74张图片](http://img.e-com-net.com/image/info8/aadd1bf58ec646a6b979b8b7eaf0a61a.jpg)
next数组的下标与字符串的下标一一对应,1~6。
- next[1]:
【当模式串的第一个字符匹配失败时,模式串指针j应该指向什么位置】
![[入门必看]数据结构4.2:串的模式匹配_第75张图片](http://img.e-com-net.com/image/info8/91f1383143e748aaab784cc5b2e5d5d7.jpg)
当第一个字符匹配失败时,直接让i++,j++,即开始匹配后一个子串和模式串:
![[入门必看]数据结构4.2:串的模式匹配_第76张图片](http://img.e-com-net.com/image/info8/e9ae5e36a72c4ba8bebba12dc76c1292.jpg)
该逻辑对于任何一个模式串都是一样的,只要第1个字符发生了不匹配的情况,只能让他匹配下一个子串。
所以所有的模式串next[1]肯定都是0。
该逻辑对于任何一个模式串都是一样的,只要第2个字符发生了不匹配的情况,应尝试匹配模式串的第1个字符。
所以所有的模式串next[2]肯定都是1。
- next[3]:
【当模式串的第三个字符匹配失败时,模式串指针j应该指向什么位置】
在不匹配的位置前划出分界线,左边的部分是已知的,右边是未知的。
尝试让模式串一步一步往右移,过程中,观察分界线左边部分能否匹配上。
直到分界线之前“能对上”,或模式串完全跨过分界线为止。
此时j指向哪儿,next数组值就是多少。
往右移动一步:![[入门必看]数据结构4.2:串的模式匹配_第82张图片](http://img.e-com-net.com/image/info8/83cbabffd1f948b0a99d6263a0d54064.jpg)
发现分界线左边的g和o失配,说明模式串右移一步不够。
继续往右移动一步:
![[入门必看]数据结构4.2:串的模式匹配_第83张图片](http://img.e-com-net.com/image/info8/022501bb72614ed389f4cd476c1afb46.jpg)
此时整个模式串跨过了分界线,此时要继续向后检查模式串的j和右边位置未知元素i是否匹配。
此时j的值为1,那么next[3] = 1
- next[4]:
【当模式串的第四个字符匹配失败时,模式串指针j应该指向什么位置】
分界线左边的值是可以确定的,逐步向右移动模式串看是否匹配,或者模式串跨过分界线。
Step4:右移三步
![]()
- next[5]:
【当模式串的第五个字符匹配失败时,模式串指针j应该指向什么位置】
最终找到了分界线左边的匹配部分,接下来检查右边i和j是否匹配:
![[入门必看]数据结构4.2:串的模式匹配_第91张图片](http://img.e-com-net.com/image/info8/760ff54c983647ed9494605d702bc171.jpg)
- next[6]:
【当模式串的第六个字符匹配失败时,模式串指针j应该指向什么位置】
最终模式串跨过分界线,之后需要检查i和模式串第1个字符能否匹配:
![[入门必看]数据结构4.2:串的模式匹配_第94张图片](http://img.e-com-net.com/image/info8/944e44392b1a480c9eb58ab3374765c8.jpg)
使⽤next数组进⾏模式匹配
给出主串S为googlo goo google,在其中找到模式串google:
![[入门必看]数据结构4.2:串的模式匹配_第96张图片](http://img.e-com-net.com/image/info8/8bcd7258b08f436ebb690d94ce5907da.jpg)
已经手算得到next数组:
![[入门必看]数据结构4.2:串的模式匹配_第97张图片](http://img.e-com-net.com/image/info8/3ebe0a88ef1948e5bedd8f5c1b69900d.jpg)
j = 6 时失配,此时让 j = next[j],即 j = next[6],
接下来让 j = 1
j = 1 时失配,此时让 j = next[j],即 j = next[1],
接下来让 j = 0
j = 5 时失配,此时让 j = next[j],即 j = next[5],
接下来让 j = 2
练习2:
求模式串T = ababaa的next数组
模式串长度是6,next组数有next[1]~next[6]![[入门必看]数据结构4.2:串的模式匹配_第105张图片](http://img.e-com-net.com/image/info8/f166b694cffb4707bf57d39b824eaed8.jpg)
总结规则:
![[入门必看]数据结构4.2:串的模式匹配_第106张图片](http://img.e-com-net.com/image/info8/dc1411828dd84c3cb52e5419cb4ae861.jpg)
Step1:next[1]=0和next[2]=1
![[入门必看]数据结构4.2:串的模式匹配_第107张图片](http://img.e-com-net.com/image/info8/8fb78d4e26b0445598d01867d8c52b2c.jpg)
Step2:求next[3]
![[入门必看]数据结构4.2:串的模式匹配_第108张图片](http://img.e-com-net.com/image/info8/cb2ecc4c21e14bab93746c2eb232ff19.jpg)
练习3:
4.2.3_KMP算法的进一步优化
——求nextval数组
KMP算法优化的思路:
以之前小节中的模式串abaabc为例,已经求出了这个模式串的next数组。
![[入门必看]数据结构4.2:串的模式匹配_第115张图片](http://img.e-com-net.com/image/info8/52506c5d849a476589221ee455553d2b.jpg)
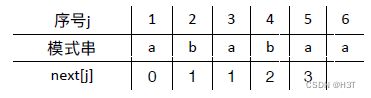
模式串abaabc的next数组:
![[入门必看]数据结构4.2:串的模式匹配_第116张图片](http://img.e-com-net.com/image/info8/ea32e71fc60c4d3aafcbcca328531836.jpg)
例1:第三个位置失配
如果第三个位置发生失配时,让j指针指回next[3]
![[入门必看]数据结构4.2:串的模式匹配_第117张图片](http://img.e-com-net.com/image/info8/b99ea9233692420db24a744cb1299a3d.jpg)
此时说明主串中第三个字符和模式串的第三个字符a是肯定不相等的。
即主串中第三个字符肯定不是a。
![[入门必看]数据结构4.2:串的模式匹配_第118张图片](http://img.e-com-net.com/image/info8/a046b1fd7e074f679ab81c881891bdaf.jpg)
如果此时按照next数组中 next[3] = 1,来进行匹配,那么这一次匹配也一定是失败的。
next[3] = 1,来进行匹配,那么这一次匹配也一定是失败的。
因为模式串中的第一个字符为a,而且已经知道了主串中的第三个字符不为a
这次匹配失败后,那么应该让j指针等于next[j],也就是等于0。
所以当第3个字符匹配失败的时候,让j = 0,即next[3] = 0。
那么下一个匹配的位置就会直接跳过这个字符,因为会让i和j同时++
![[入门必看]数据结构4.2:串的模式匹配_第122张图片](http://img.e-com-net.com/image/info8/7680832855ad45ed9c138fe16603b6a2.jpg)
例2:第五个位置失配
假设模式串在第5个位置失配,那么KMP算法会让j = next[5] = 2。
![[入门必看]数据结构4.2:串的模式匹配_第123张图片](http://img.e-com-net.com/image/info8/c1f4effd5b2e4e00aef8f43e39651cd7.jpg)
虽然暂时不知道主串i指针所指位置的字符是什么,但是肯定不是b。
![[入门必看]数据结构4.2:串的模式匹配_第124张图片](http://img.e-com-net.com/image/info8/32f8e5d19ce541b185154f862abbd4ec.jpg)
所以如果按照刚才让j指针指向2位置,接下来的这次匹配一定是失败的,因为字符2和字符5都是b,然后还需要让j = next[2] = 1。
所以干脆就一步到位,让next[5] =next[2]的值:
即j = next[5] = 1:
此时回到上面的情况,如果字符5发生失配,j = next[5],直接就j = 1,节约了一个步骤,没有必要再让next[5] = 2,即比较第二个字符,因为肯定匹配不上。
这就是优化。
当然不是所有next数组都可以优化,优化思路为:
需要判断next数组所指的字符和原本失配的字符是否相等。
- 如果这两个字符不相等,那么next数组保持不变;
- 如果这两个字符相等,那么next数组就可以进行优化。
![[入门必看]数据结构4.2:串的模式匹配_第125张图片](http://img.e-com-net.com/image/info8/6fc08cd9dc29450b98ff313e38a4dc72.jpg)
将next数组优化成nextval,然后再KMP算法匹配的时候,用nextval数组替代next数组,其他一样。
练习1:
![[入门必看]数据结构4.2:串的模式匹配_第126张图片](http://img.e-com-net.com/image/info8/a463638b2e544cbb81c24d3dfc2f36ef.jpg)
然后手算其nextval数组:
![[入门必看]数据结构4.2:串的模式匹配_第127张图片](http://img.e-com-net.com/image/info8/d32d366c099f41529384556f777eba27.jpg)
首先,nextval[1]的值直接写=0;
然后,如果当前的next[j]所指字符,和目前j所指的字符不相等,就让nextval的值等于next的值,所以nextval[2]应该等于1。
- 如,next[2] = 1,所指字符为第1个,即a,和目前j所指的第2个字符b不相等,那么nextval[1] = next[1] = 1
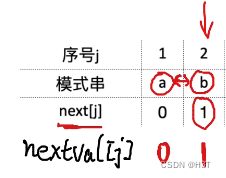
- 如,next[3] = 1,所指字符为第1个,即a,但是目前j所指第3个字符为a相等,那么就让nextval[3] = nextval[next[3]] = nextval[1] = 0,即跳到1对比失败的那个next,即next[1] = 0。
也就是说直接把next[3]的值优化为next[1]的值,即0。
![[入门必看]数据结构4.2:串的模式匹配_第128张图片](http://img.e-com-net.com/image/info8/c0065737eb8f4708915bd1476e7428ad.jpg)
同样的,第四个字符b失配时,next[4] = 2,跳到第二个字符b时相等,那么
nextval[4] = nextval[next[4]] = nextval[2] = 1
![[入门必看]数据结构4.2:串的模式匹配_第129张图片](http://img.e-com-net.com/image/info8/5a99dc61aeed40b09b9dedc73fc3e60d.jpg)
第五个字符a失配时,next[5] = 3,跳到第三个字符a时相等,那么
nextval[5] = nextval[next[5]] = nexvalt[3] = 0
第六个字符a失配时,next[6] = 4,跳到第四个字符b时不相等,那么
nextval[6] = next[6] = 4
![[入门必看]数据结构4.2:串的模式匹配_第130张图片](http://img.e-com-net.com/image/info8/7e9e48dc8edf4c64a0e1209283ae8be9.jpg)
最终求出了nextval数组:
![[入门必看]数据结构4.2:串的模式匹配_第131张图片](http://img.e-com-net.com/image/info8/d2a62f55868a47c4ad0d6ee4f212e45f.png)
练习2:
对于模式串:
![[入门必看]数据结构4.2:串的模式匹配_第132张图片](http://img.e-com-net.com/image/info8/face97d1dded46ebb4685aaedf07d001.jpg)
其next数组是:
![[入门必看]数据结构4.2:串的模式匹配_第133张图片](http://img.e-com-net.com/image/info8/5e812012917a4915b469cec1ff240776.jpg)
nextval[1] = 0;
第二个字符和next[2]所指字符相等,nextval[2] = nextval[next[2]] = 0;
第三个字符和next[3]所指字符相等,nextval[3] = nextval[next[3]] = 0;
第四个字符和next[4]所指字符相等,nextval[4] = nextval[next[4]] = 0;
第五个字符和next[5]所指字符不相等,nextval[5] = [next[5] = 4。
所以求得其nextval数组为:
优化KMP算法
——感受一下优化的力量
优化前:
![[入门必看]数据结构4.2:串的模式匹配_第135张图片](http://img.e-com-net.com/image/info8/ee9fd176f3fb4ce18fce99c24746caa0.jpg)
此时匹配到第4个字符,失配。到next[4] = 3:
![[入门必看]数据结构4.2:串的模式匹配_第136张图片](http://img.e-com-net.com/image/info8/f4b4850d2f2940c5a7146d80119003d2.jpg)
此时第3个字符依然失配。到next[3] = 2:
![[入门必看]数据结构4.2:串的模式匹配_第137张图片](http://img.e-com-net.com/image/info8/c11a2273fefa4749a8b74d0cabadfaf3.jpg)
此时第2个字符依然失配。到next[2] = 1:
![[入门必看]数据结构4.2:串的模式匹配_第138张图片](http://img.e-com-net.com/image/info8/3c189d63da8747ba9e179d7b2b449540.jpg)
此时第1个字符依然失配。到next[1] = 0:
![[入门必看]数据结构4.2:串的模式匹配_第139张图片](http://img.e-com-net.com/image/info8/c2ec2d51373e4cd0b5f848ad11b082e4.jpg)
j = 0时,i和j同时++:
![[入门必看]数据结构4.2:串的模式匹配_第140张图片](http://img.e-com-net.com/image/info8/3c87e9f0f9db402b855b1af45d1caf5a.jpg)
此时匹配成功:
![]()
优化后:
![[入门必看]数据结构4.2:串的模式匹配_第141张图片](http://img.e-com-net.com/image/info8/11d9f851f80e400694a25d8621225f31.jpg)
此时匹配到第4个字符,失配。到nextval[4] = 0:
![[入门必看]数据结构4.2:串的模式匹配_第142张图片](http://img.e-com-net.com/image/info8/daa59704ab4c4e1d909f3056c86da4a7.jpg)
j = 0时,i和j同时++:
![[入门必看]数据结构4.2:串的模式匹配_第143张图片](http://img.e-com-net.com/image/info8/cd0b22a948fa45bf934bb4861eab8b2d.jpg)
此时就跳过了刚才中间部分的对比。
把next数组优化为nextval数组之后,中间减少了很多没有必要的对比。
知识回顾与重要考点
4.2.1_朴素模式匹配算法
- 暴力解法:把所有有可能的子串遍历一遍
- 最坏时间复杂度 = O ( n m ) O(nm) O(nm)
——每一个子串前面所有元素都和模式串匹配,只有最后一个元素和模式串不匹配
4.2.2_1_KMP算法
- 需要掌握手算next数组的方法
- 记住KMP算法的整体时间复杂度 O ( m + n ) O(m+n) O(m+n)
——预处理(next数组)时间复杂度 O ( m ) O(m) O(m);模式匹配时间复杂度 O ( n ) O(n) O(n)
4.2.2_2_求next数组
4.2.3_KMP算法的进一步优化
- 串在考试中的地位
![[入门必看]数据结构4.2:串的模式匹配_第1张图片](http://img.e-com-net.com/image/info8/ffe0d5a57c204d78bb27c7c8df2c67d5.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第2张图片](http://img.e-com-net.com/image/info8/64711cad16774f3da463d48d3a7d610b.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第3张图片](http://img.e-com-net.com/image/info8/5c9679603520466885ef9cbcd729ac8e.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第4张图片](http://img.e-com-net.com/image/info8/b8aaaa5046ee4957974da38c3ceb8563.jpg)

![[入门必看]数据结构4.2:串的模式匹配_第7张图片](http://img.e-com-net.com/image/info8/3519c6eff707478e8d6cccca1ea58d2c.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第8张图片](http://img.e-com-net.com/image/info8/7f4ee5730fd24018a61ba514df484822.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第9张图片](http://img.e-com-net.com/image/info8/82b3976647dd425087a84cf508e2dc22.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第10张图片](http://img.e-com-net.com/image/info8/6447aac6b10c47c38f8f04c913619f3a.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第11张图片](http://img.e-com-net.com/image/info8/4c6cf6ff3b2446258f82ee4a5fd76bfb.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第12张图片](http://img.e-com-net.com/image/info8/5bf7e612aa1d4b72901c6659300df9a3.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第13张图片](http://img.e-com-net.com/image/info8/89f4d12e6092471aa22152cf5802188d.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第14张图片](http://img.e-com-net.com/image/info8/50a6a96575174a7f9a7287fcbbd6ff36.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第15张图片](http://img.e-com-net.com/image/info8/e78319ea65f8432298be38a9d950b406.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第16张图片](http://img.e-com-net.com/image/info8/40cacd1b537b40dda4a43a2dfef33a48.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第40张图片](http://img.e-com-net.com/image/info8/c9a117aaed9a46829cc04e434fc31ca0.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第41张图片](http://img.e-com-net.com/image/info8/43252d91f2b54478b25c0b0a29e72341.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第42张图片](http://img.e-com-net.com/image/info8/8f6b7b4962b84e3c9687a4fb58c9cf84.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第43张图片](http://img.e-com-net.com/image/info8/1595be94d2214f2597202fb39792b614.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第44张图片](http://img.e-com-net.com/image/info8/09b01a3be2cd4d6a91265cf2714e6853.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第45张图片](http://img.e-com-net.com/image/info8/938a9354b76f433c9017d5bdb7ef7e75.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第46张图片](http://img.e-com-net.com/image/info8/253dd29c1a4645eaa85affef81671665.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第47张图片](http://img.e-com-net.com/image/info8/6532241967264934a5c9b585c2d0597d.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第48张图片](http://img.e-com-net.com/image/info8/4dc2cf01d3244ca18bacb6fcbedca49c.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第49张图片](http://img.e-com-net.com/image/info8/5a4df16231394aae8e35a160d9ed4e1e.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第50张图片](http://img.e-com-net.com/image/info8/b89fc7055d034e5a9eee9de683223189.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第51张图片](http://img.e-com-net.com/image/info8/1208bd8dc8e1409d93a07fd724a64ce0.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第52张图片](http://img.e-com-net.com/image/info8/e87433b10db04c2b84141baca9f2006a.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第53张图片](http://img.e-com-net.com/image/info8/b029c1739872477bbebd129d429c21fe.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第54张图片](http://img.e-com-net.com/image/info8/97e7d74108d444469ce15866c387fb7e.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第55张图片](http://img.e-com-net.com/image/info8/b18ea06209b94b42805573db17bafdf1.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第56张图片](http://img.e-com-net.com/image/info8/5a766255ad574295b19d1e983b444332.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第57张图片](http://img.e-com-net.com/image/info8/877491eca247400fb63704fa1388857a.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第58张图片](http://img.e-com-net.com/image/info8/4c4fd94e01d845af806cca7ddbd883aa.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第59张图片](http://img.e-com-net.com/image/info8/311406135e4240da8f11b436087c37cf.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第60张图片](http://img.e-com-net.com/image/info8/821697c7a7e840f1bd61b0c61507e492.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第61张图片](http://img.e-com-net.com/image/info8/7797853561e54d44a535efa4a487b856.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第62张图片](http://img.e-com-net.com/image/info8/1314bb80d63147b8920b4f7e7e00baff.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第63张图片](http://img.e-com-net.com/image/info8/79928007e74f45d6a2dde6d8231da5a3.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第64张图片](http://img.e-com-net.com/image/info8/ddb3ddd0a78d46c0b4f9282f6905a424.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第65张图片](http://img.e-com-net.com/image/info8/4c57cb7db3b449fab57289b9601d0479.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第66张图片](http://img.e-com-net.com/image/info8/1af2bc4d60db4f9784f549e35ad6efb6.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第67张图片](http://img.e-com-net.com/image/info8/5f95044fc8b54684ad703106039d92ff.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第68张图片](http://img.e-com-net.com/image/info8/744716c493b2416d916552bf259d2a5a.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第72张图片](http://img.e-com-net.com/image/info8/e84b0256a6dd4ae8ad7253214ae80b23.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第77张图片](http://img.e-com-net.com/image/info8/cac9d946ca724f18b76c3c1cc3da407d.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第78张图片](http://img.e-com-net.com/image/info8/00d9bf681c65403c829273eee323a608.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第79张图片](http://img.e-com-net.com/image/info8/6903b073973249d681f4fb8a5cdea55e.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第80张图片](http://img.e-com-net.com/image/info8/28947ba7a1534deba1f22890f754b6de.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第81张图片](http://img.e-com-net.com/image/info8/547c46630941428b9c8aec2a2a037aea.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第84张图片](http://img.e-com-net.com/image/info8/d27584d9880c4266b313b929d949a95f.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第85张图片](http://img.e-com-net.com/image/info8/336967dda3c847d2979a2bd3e51a629a.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第86张图片](http://img.e-com-net.com/image/info8/aa0402e83211456087b3d61c6d57531b.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第87张图片](http://img.e-com-net.com/image/info8/c49ace790b3f4ab9962300543138c438.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第88张图片](http://img.e-com-net.com/image/info8/351f3ecd0e8f41bd84821042f86c641e.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第89张图片](http://img.e-com-net.com/image/info8/bd3133ab21c24de0a462db709d4f98b2.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第90张图片](http://img.e-com-net.com/image/info8/06a516bd305d43e283f0c3f58a934c6d.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第92张图片](http://img.e-com-net.com/image/info8/ba7ced13ec4e42928072d80cd5ecef24.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第93张图片](http://img.e-com-net.com/image/info8/bc4fc405fa6144e1a503104d803a0e3f.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第98张图片](http://img.e-com-net.com/image/info8/fb524fa091b149eabcdba5bca80adf5a.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第99张图片](http://img.e-com-net.com/image/info8/bc653071be724481ba860e57acb85b73.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第100张图片](http://img.e-com-net.com/image/info8/419df41e90434c5580b04a7eab56cc91.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第101张图片](http://img.e-com-net.com/image/info8/33242ddae38c4dc381ac10fbf295a7ce.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第102张图片](http://img.e-com-net.com/image/info8/4a880dbedb6644639e672e1fc5aecb71.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第103张图片](http://img.e-com-net.com/image/info8/8b49a2faf96b43df9b123cdc42f554b7.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第104张图片](http://img.e-com-net.com/image/info8/5bb97204db4e47a0ad6b746cf87bbab4.jpg)

![[入门必看]数据结构4.2:串的模式匹配_第109张图片](http://img.e-com-net.com/image/info8/dfb030731fcd47c2851a26b88d2335bc.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第110张图片](http://img.e-com-net.com/image/info8/84ad1d5605244f649da0fcc76652abd7.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第111张图片](http://img.e-com-net.com/image/info8/afba4d9f372f43f087fbd4cfd247ca99.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第112张图片](http://img.e-com-net.com/image/info8/af54e39dafd84ac2b77d9e26b0a55471.jpg)

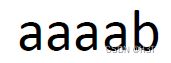
![[入门必看]数据结构4.2:串的模式匹配_第113张图片](http://img.e-com-net.com/image/info8/d0641e815eb64fa08303e6eb2fee44ff.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第114张图片](http://img.e-com-net.com/image/info8/93cf9b0258f641fdbe955a2891a9f3d3.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第119张图片](http://img.e-com-net.com/image/info8/bded384795934947a2ab5499477157ce.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第120张图片](http://img.e-com-net.com/image/info8/46e306eb030840dd8da79c3afb7e0228.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第121张图片](http://img.e-com-net.com/image/info8/0f3cade5b6e24333b817f3f018b4bc22.jpg)
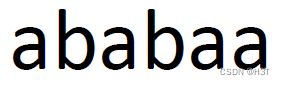
![[入门必看]数据结构4.2:串的模式匹配_第134张图片](http://img.e-com-net.com/image/info8/dbaba0e5d29f4b5cb6f52b0733f28fd6.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第144张图片](http://img.e-com-net.com/image/info8/620e5eb284844805999ab6eccdc5ae1f.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第145张图片](http://img.e-com-net.com/image/info8/b5c66ebd945e43e4868733674373f699.jpg)
![[入门必看]数据结构4.2:串的模式匹配_第147张图片](http://img.e-com-net.com/image/info8/b665b56f85b448dca09073c9b41507e9.jpg)