NeurIPS 2017 | GraphSAGE:大型图的归纳表示学习
目录
- 前言
- 1. 引言
- 2. GraphSAGE
-
- 2.1 嵌入生成算法
- 2.2 聚合器
- 2.3 泛化到新节点
- 2.4 GraphSAGE的参数学习
- 3. 后记
前言

题目: Inductive Representation Learning on Large Graphs
会议: NeurIPS 2017
论文地址:Inductive Representation Learning on Large Graphs
关于图嵌入算法前面讲过很多了:
- KDD 2016 | node2vec:Scalable Feature Learning for Networks
- KDD 2014 | DeepWalk: 社会表征的在线学习
- WWW 2015 | LINE:大规模信息网络的嵌入
- KDD 2016 | SDNE:结构化深层网络嵌入
从论文题目可以看出,GraphSAGE是一种归纳(Inductive)学习的模型,而前面讲的几种算法属于Transductive learning,也就是直推式学习。
所谓归纳学习,是指我们在得到一个新节点时,可以直接根据其邻接关系来计算出其嵌入表示。比如在GraphSAGE中,我们可以根据聚合函数来算出新节点的嵌入表示。
而在直推学习中,我们需要将新节点的信息经过网络重新训练,然后才能得到其嵌入表示。也就是说,直推式学习只能够在一张固定的图上来学习节点的嵌入表示,并不能直接泛化到未知节点,也不能够跨图进行节点表示学习。
GraphSAGE是对上一篇提到的GCN的扩展,其主要有两个方面的改进:
- 通过一种采样策略改善了GCN中的full batch,变成了mini batch,减少了计算量,这使得大图的分布式训练成为可能。
- 引入了聚合函数,对卷积进行了扩展。
1. 引言
大型图中节点的低维嵌入表示对各种图任务有着很重要的作用。节点嵌入方法的基本思想是使用降维技术将节点图邻域的高维信息提取到稠密向量嵌入中。然后,这些节点嵌入可以反馈给下游机器学习系统,并帮助完成节点分类、聚类和链接预测等任务。
前面我们讲到了GCN,GCN结合了每个节点的特征信息和其邻居节点的信息来对学习节点的嵌入表示,并且相比传统图卷积,GCN增加了自环,这可以使得节点向量在更新过程中还可以考虑自己的特征信息。但GCN有一个问题:无法直接泛化到训练过程中没有出现过的节点,属于一种直推式(transductive)的学习。也就是说,如果出现一个新的节点,并且其邻居关系也确定了,那我们需要重新训练以得到新节点的嵌入表示。
然而,许多实际应用需要为看不见的节点或全新(子)图快速生成嵌入。这种归纳能力对于高通量生产型机器学习系统至关重要。生成节点嵌入的归纳方法也有助于在具有相同特征形式的图之间进行泛化:例如可以在从模型生物衍生的蛋白质-蛋白质相互作用图上训练嵌入生成器,然后使用经过训练的模型,轻松地为收集到的新生物体数据生成节点嵌入。
本文的贡献就是提出了一个具有归纳能力的图表示学习框架GraphSAGE(SAmple and aggreGatE),将GCN扩展到归纳无监督学习的任务。
2. GraphSAGE
本节分为三部分:第一部分描述了如何生成节点的嵌入表示,第二部分描述了如何使用SGD和反向传播来学习模型的参数,第三部分描述了如何将结果泛化到新节点。
2.1 嵌入生成算法
嵌入生成算法也就是前向传播,算法伪代码描述如下:

输入:图 G ( V , E ) G(V,E) G(V,E);每个节点的特征向量 x v x_v xv;深度 K K K;第k层权重矩阵 W k W^k Wk;非线性激活函数 σ \sigma σ;可微聚合函数 A G G R E G A T E k AGGREGATE_k AGGREGATEk;邻居函数 N N N。
输出:每个节点的嵌入表示。
算法1的主要思想:在每次迭代时,节点都会聚合来自其局部邻居的信息,并且随着该过程的迭代,节点会逐渐从图的更远处获得越来越多的信息。
首先初始时,每个节点的表示向量就是其特征向量 x v x_v xv。然后我们一共迭代 K K K次(K层神经网络),其中每一层迭代:
- 每一个节点都首先聚合其邻居节点上一层迭代结束时得到的表示向量,以得到一个single vector。
- 每一个节点将聚合得到的向量和自己上一层迭代结束时得到的表示向量进行concat操作,然后乘上本层的参数 W k W^k Wk,再经过一个激活函数,最终得到本层迭代结束后该节点的表示向量。
经过 K K K次迭代后,每个节点都得到了最终的表示向量,也就是其嵌入向量。
为了将上述算法扩展到mini batch,给定一组输入节点,我们首先需要向前采样所需的邻域集(深度K),然后再进行聚合。 也就是说,算法中的 N ( v ) N(v) N(v)并不是传统意义上节点 v v v的邻居,而是经过采样得到的邻居,这也是处于计算效率的考虑,因为在一些大型图中可能某些节点有上百万个邻居。当然,把所有邻居都考虑到当然是最好的,不过为了推广到大型图,考虑所有邻居显然是不现实的。
我们首先回忆一下GCN的原理:

在GCN中,对于某一个中心节点,其经过第一层卷积时,只需要提取其一阶邻居的信息;当经过第二层卷积时,其同样提取其邻居节点的信息,但此时其邻居节点由于同样经过了第一层卷积,此时其表示向量中也包含了其邻居节点的信息,也就是说中心节点此时提取了其邻居的邻居的信息。
假设图中节点的平均度是 d d d,一共需要经过 K K K个GCN层,那么一共需要纳入的节点数量为: 1 + d + d 2 + . . . + d K 1+d+d^2+...+d^K 1+d+d2+...+dK。可以发现,随着层数加深,需要纳入的节点数呈指数级增长,导致计算复杂度极高,同时会存在某些节点的度非常大,就会进一步放大指数问题,导致高阶的特征计算成本昂贵。
与GCN不同,在GraphSAGE中,我们会对每一层节点采样设置采样倍率 S k S_k Sk,比如 S 1 = 3 , S 2 = 5 S_1=3,S_2=5 S1=3,S2=5,那么每一个节点在进行第一层迭代时,采样的节点数量为3个,在进行第二层迭代时,采样的节点数量为5个。如下所示:

上图中GraphSAGE在第一层采样时只选择了3个邻居节点,第二层选择了5个邻居节点。
具体来讲,对于一个节点,我们首先列出与之关联的所有节点,然后从这些节点中进行采样(可允许重复),直到得到我们想要的节点数量。
2.2 聚合器
由于节点的邻居没有自然的顺序,因此算法1中的聚合器函数必须能有效地在一组无序的向量上运行。理想情况下,聚合器函数应该是对称的(即对输入的排列不变),同时仍然是可训练的,并保持较高的表示能力。聚合函数的对称性确保了神经网络模型可以训练并应用于任意顺序的节点邻域特征集。
本文主要研究了三个聚合器函数:
(1)Mean aggregator
未经扩展的均值聚合:先将节点的邻居节点取平均,然后再与该节点的向量进行concat操作,然后再来一个非线性转换。
作者将均值聚合进行改进:
![]()
可以发现,改进后的均值聚合不再将邻居节点的平均值和节点向量concat,而是直接对该节点和其邻居节点求平均。文章中称这种改进的基于均值的聚合器为卷积,因为它是局部光谱卷积的粗略线性近似。该卷积聚合器与本文提出的其他聚合器之间的一个重要区别:均值聚合不执行算法1第5行中的concat操作。
(2)LSTM aggregator:LSTM是处理顺序数据的,不具备排列不变性。在利用LSTM聚合器对邻居节点进行聚合前,简单地将其随机打乱,来使LSTM适应于在无序集上操作 。
(3)Pooling aggregator:与前面两个聚合器不同,池化聚合器同时具有对称和可训练的性质。其操作如下:
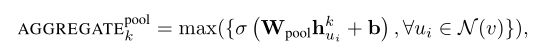
节点的所有邻居的向量首先通过一个神经网络得到输出,然后再求这些输出的最大值。
2.3 泛化到新节点
在LINE中,我们对新节点的处理方式为:对于一个新的节点 i i i,如果我们已知它和其它已有节点的连接情况,那么我们就可以得到经验分布 p 1 ^ ( ⋅ , v i ) \hat{p_1}(\cdot,v_i) p1^(⋅,vi)和 p 2 ^ ( ⋅ ∣ v i ) \hat{p_2}(\cdot|v_i) p2^(⋅∣vi),然后我们就可以优化 O 1 O_1 O1或者 O 2 O_2 O2:
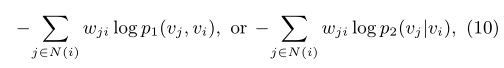
通过更新新节点的嵌入,保持已有节点的嵌入,我们就能得到新节点的嵌入表示。
如果我们无法观察到新节点与其他节点的连接情况,我们就必须依靠其他信息,比如节点的文本信息。
而在GraphSAGE中,我们可以直接根据聚合函数和新节点邻居节点的嵌入表示来计算得到新节点的嵌入表示。
2.4 GraphSAGE的参数学习
在节点通过多层迭代后得到了每个节点的嵌入表示后,我们就可以计算损失了。损失函数根据具体应用场景,可以分为基于图的无监督损失和有监督损失。
首先是基于图的无监督损失:
![]()
其中 z u z_u zu是节点 u u u的嵌入表示,节点 v v v是节点 u u u进行random walk访问到的节点。
有监督损失:比如在分类任务中可以使用交叉熵损失。
有了损失函数后就可以反向对参数求梯度,然后更新参数,进行新一轮的迭代。
3. 后记
实验部分就不再详细讲了,有兴趣可以自己钻研一下。代码也不复现了,PyG上有GraphSAGE的封装实现,可以直接调包。