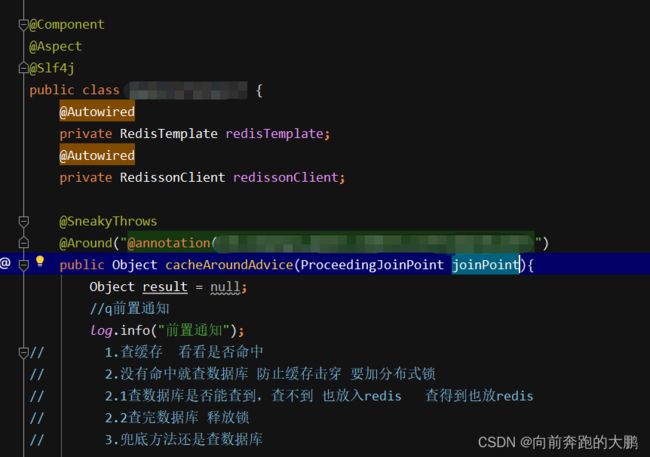
分布式锁 + AOP实现缓存
随着业务中缓存及分布式锁的加入,业务代码变的复杂起来,除了需要考虑业务逻辑本身,还要考虑缓存及分布式锁的问题,增加了程序员的工作量及开发难度。而缓存的玩法套路特别类似于事务,而声明式事务就是用了aop的思想实现的。
一、思路
创建一个自定义注解,创建一个切面类。
在切面类中切入点的判断用
"@annotation(注解全类名)"
二、缓存的实现
在切面类中,实现对切入点的方法增强,这也是aop的重要思想(对原有代码只做增强,不做修改)。被修饰的方法是直接查询数据库的,这样产生的问题就有很多,例如 缓存穿透、缓存雪崩、缓存击穿。因此要用分布式锁,对查询数据库做一个保障。
思路:
// 1.查缓存 看看是否命中 // 2.没有命中就查数据库 防止缓存击穿 要加分布式锁 // 2.1查数据库是否能查到,查不到 也放入redis 查得到也放redis // 2.2查完数据库 释放锁 // 3.兜底方法还是查数据库
分布式锁,可以解决缓存击穿的问题,布隆过滤器可以解决缓存穿透问题。
分布式锁,简单来讲就是在redis缓存中创建一个键,键名就是锁名,如果缓存中存在,就不能创建,这就是没获取到锁。锁创建成功,拿到锁以后,再做数据库的查询,查完释放锁(就是删除键名)
分布式锁的实现一般用RedissonClient创建。
RLock lock = redissonClient.getLock(键名)
lock.lock()
lock.unlock()
三、AOP
横向提取,动态织入
5、布隆过滤器
5.1 布隆过滤器原理
5.1.1 什么是布隆过滤器
布隆过滤器(Bloom Filter),是1970年,由一个叫布隆的小伙子提出的,距今已经五十年了。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。二进制大家应该都清楚,存储的数据不是0就是1,默认是0。
主要用于判断一个元素是否在一个集合中,0代表不存在某个数据,1代表存在某个数据。
总结: 判断一个元素一定不存在 或者 可能存在! 存在一定的误判率{通过代码调节}
Bit 数组:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|
5.1.2 布隆过滤器使用场景
大数据量的时候, 判断一个元素是否在一个集合中。解决缓存穿透问题
5.1.3 原理
存入过程
布隆过滤器上面说了,就是一个二进制数据的集合。当一个数据加入这个集合时,经历如下:
通过K个哈希函数计算该数据,返回K个计算出的hash值
这些K个hash值映射到对应的K个二进制的数组下标
将K个下标对应的二进制数据改成1。
如图所示:
查询过程
布隆过滤器主要作用就是查询一个数据,在不在这个二进制的集合中,查询过程如下:
1、通过K个哈希函数计算该数据,对应计算出的K个hash值
2、通过hash值找到对应的二进制的数组下标
3、判断:如果存在一处位置的二进制数据是0,那么该数据不存在。如果都是1,该数据可能存在集合中。
5.1.4 布隆过滤器的优缺点
优点
-
由于存储的是二进制数据,所以占用的空间很小
-
它的插入和查询速度是非常快的,时间复杂度是O(K),空间复杂度:O (M)。
-
K: 是哈希函数的个数
-
M: 是二进制位的个数
-
-
保密性很好,因为本身不存储任何原始数据,只有二进制数据
缺点
-
添加数据是通过计算数据的hash值,那么很有可能存在这种情况:两个不同的数据计算得到相同的hash值。
例如图中的“张三”和“张三丰”,假如最终算出hash值相同,那么他们会将同一个下标的二进制数据改为1。
这个时候,你就不知道下标为1的二进制,到底是代表“张三”还是“张三丰”。
由此得出如下缺点:
一、存在误判
假如上面的图没有存 "张三",只存了 "张三丰",那么用"张三"来查询的时候,会判断"张三"存在集合中。
因为“张三”和“张三丰”的hash值是相同的,通过相同的hash值,找到的二进制数据也是一样的,都是1。
误判率:
受三个因素影响: 二进制位的个数m, 哈希函数的个数k, 数据规模n (添加到布隆过滤器中的函数)
已知误判率p, 数据规模n, 求二进制的个数m,哈希函数的个数k {m,k 程序会自动计算 ,你只需要告诉我数据规模,误判率就可以了}
ln: 自然对数是以常数e为底数的对数,记作lnN(N>0)。在物理学,生物学等自然科学中有重要的意义,一般表示方法为lnx。数学中也常见以logx表示自然对数。
二、删除困难
还是用上面的举例,因为“张三”和“张三丰”的hash值相同,对应的数组下标也是一样的。
如果你想去删除“张三”,将下标为1里的二进制数据,由1改成了0。
那么你是不是连“张三丰”都一起删了呀。