KMP字符串匹配算法

如有错误，感谢不吝赐教、交流

一、问题引入:

leetcode28
给你两个字符串 txt 和 pat ，请你在 txt 字符串中找出 pat 字符串的第一个匹配项的下标（下标从 0 开始）。如果 pat 不是 txt 的一部分，则返回 -1 ，后面统一用这种方式的记号。

问题示例一：

假设对于文本串txt：“aabaabaaf” 长度为n
模式串pat：“aabaaf” 长度为m
求模式串pat出现在文本串txt中的位置?

问题示例二：

假设对于文本串txt：“mississippi” 长度为n
模式串pat：“issipi” 长度为m
求模式串pat出现在文本串txt中的位置?

问题示例三：

假设对于文本串txt：“aaaaaac” 长度为n
模式串pat：“aaaaac” 长度为m
求模式串pat出现在文本串txt中的位置?

问题示例四：txt长度小于pat长度

假设对于文本串txt：“aaaaaac” 长度为n
模式串pat：“aaaaacaaaa” 长度为m
求模式串pat出现在文本串txt中的位置?
直接返回-1

Java实现BruteForce

public static int solution(String txt, String pat) {
        // txt是搜索串
        // pat是模式串
        int txt_length = txt.length();
        int pat_length = pat.length();
        if (txt_length < pat_length) {
            return -1;
        }
		// 长度超了直接就不匹配了
        for (int i = 0; i <= txt_length - pat_length; i++) {

            for (int j = 0; j < pat_length; j++) {
                if (txt.charAt(i + j) != pat.charAt(j)) {
                    break;  // 跳出内循环
                }

                // 匹配成功
                if (j == pat_length - 1) {
                    return i;  // 匹配成功，返回此时txt字符串中的起始位置
                }
            }

        }
        return -1;
    }

相对于暴力匹配，我们发现，有些已经匹配的信息是可以利用的，只是需要确定模式串跳转到哪个位置，于是乎，见KMP算法。

KMP

Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串P 的出现位置。

前缀表（next数组）

核心是记录在模式串和文本串不匹配之后，模式串应该跳转到那个位置开始继续匹配。
有不同求next数组的方法，核心都是一样的，只要理解核心，就能解题。

怎么求next数组

什么是前缀：模式串P中最后一个字符串之前的字符串的顺序组合
如对于模式串P：“aabaaf”
前缀为：“a”、“aa”、“aab”、“aaba”、“aabaa”
什么是后缀：模式串P中第一个字符串之后的字符串的顺序组合
后缀为：“f”、“af”、“aaf”、“baaf”、“abaaf”

求最长相等前后缀
这里直接看图说话吧，会更加清晰，看了还不会，那应该是我没有描述清楚，但我相信看了一定会，因为我就是这样理解了的。

示例一：模式串“aaaaac”的next数组

定义next数组长度为：“aaaaac”.length() - 1; 如下图所示：

“aaaaac”的前缀：
“a”:

即如果模式串第0个字符与文本串就不相等，那么下一次用文本串的下一个位置与模式串的0号位置匹配判断
“aa”:

即如果模式串第1个字符与文本串就不相等，那么下一次用文本串的当前位置与模式串的1号位置匹配判断
“aaa”:

这张图，更能说明如何求最长相等前后缀，即对于“aaa”来说，它的最长相等前后缀长度为2，如蓝线框所示。
“aaaa”:

同理可得
“aaaaa”:

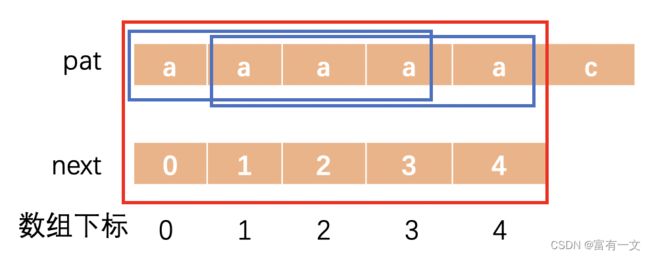
第一个例子看了，可能有点懵，不急，多看几个就知道怎么求了。

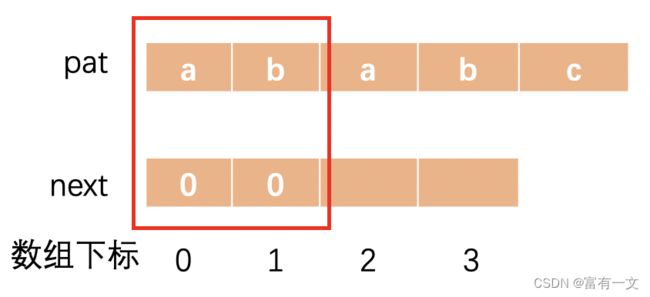
示例二：模式串“ababc”的next数组

初始化next数组：

对于前缀：
“a”:

“ab”:

“aba”:

“abab”:

通过示例二是不是更加清楚了，再看示例三

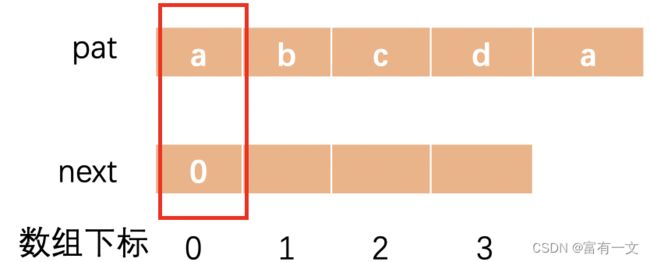
示例三:模式串“abcda”的next数组

初始化next:

所有前缀：
“a”:

“ab”:

“abc”:

“abcd”:

是不是有一点奇怪，为什么模式串中又两个’a’为什么next数组全是0，这里我们思考一下，如果是判断到第二个’a’匹配成功则返回，不匹配，是不是应该从第一个’a’重新匹配判断。
不同的计算方式求得next数组结果不一样，有的右移有的左移，选择一种自己容易理解就行，而且只是在匹配逻辑判断后的跳转方式略微不同。
接下来我们看看如何利用计算得出来的next数组进行解答。

如何使用前缀表求解问题

示例：txt=“aabaabaaf”，pat=“aabaaf”

如图，第一次判断到txt的‘b’和pat的’f’时，两者不相等，记pat的索引为pat_index = pat.length() - 1;此时，修改pat_index = next[pat_index - 1]，即相当于判断pat的‘b’字符与txt的’b’字符，因为已经记录他们前面的"aa"是相等的，这就是next数组的魅力，在匹配不成功是给出跳转到哪里重新开始匹配。在上面的暴力方法中，我们是模式串回到最开始的位置进行判断，kmp妙就在这里。

问题解决。不清楚的话，多画几个例子就知道了。

代码示例：

求next数组：

很傻的一种求next数组的方式，但是很好理解

// 很傻的一种求next数组的方式
        for (int i = 1; i < next_length; i++) {
            p_r = i+1;  // p_r 等于最右边，这里为了方便java获取字符串比较，故加1
            for (int j = 1; j <= i; j++) {
                if (pat.substring(p_l, p_l+j).equals(pat.substring(p_r - j, p_r))) {
                    next[i] = j;
                }
            }
        }

换一种更优的方法，有一点需要理解是怎么转换的过程，多搞几个例子画一下

        for(int i = 1, j = 0; i < next_length; i++) {
            while (j >0 && pat.charAt(i) != pat.charAt(j)) {
                j = next[j-1];
            }
            if (pat.charAt(i) == pat.charAt(j)) {
                j++;
            }
            next[i] = j;
        }

leetcode28

leetcode28

public int strStr(String haystack, String needle) {
        int n = haystack.length(), m = needle.length();
        if (m == 0) {
            return 0;
        }
        int[] pi = new int[m];
        for (int i = 1, j = 0; i < m; i++) {
            while (j > 0 && needle.charAt(i) != needle.charAt(j)) {
                j = pi[j - 1];
            }
            if (needle.charAt(i) == needle.charAt(j)) {
                j++;
            }
            pi[i] = j;
        }
        for (int i = 0, j = 0; i < n; i++) {
            while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
                j = pi[j - 1];
            }
            if (haystack.charAt(i) == needle.charAt(j)) {
                j++;
            }
            if (j == m) {
                return i - m + 1;
            }
        }
        return -1;
    }

leetcode459

leetcode459
核心想法：P + P + P。。。的一个以P重复组合构成
那么最长相等前后缀是不是应该是这样的一种情况
假如txt = P + P + P构成，那么最后相等前后缀就是P + P
假如txt = P + P + P+P构成，那么最后相等前后缀就是P + P+ P
假如txt = P + P + P+ P+ P构成，那么最后相等前后缀就是P + P+ P + P
即始终差着一个P，通过这样判断txt由P重复组成

如果是txt = P + a + P，那么最长相等前后缀为P,但是txt - P != P ，还差着一个a，所以返回false 代码如下，很简单

public boolean repeatedSubstringPattern(String s) {
        int length = s.length();
        int [] next = new int[length];

        for (int i = 1, j = 0; i < length; i++) {
            while(j > 0 && s.charAt(i) != s.charAt(j)) {
                j = next[j -1];
            }

            if (s.charAt(i) == s.charAt(j)) {
                j++;
            }  

            next[i] = j;
        }

        if (next[length-1] != 0 && length %(length - next[length-1])  == 0) {
            return true;
        }
        return false;
    }

ps:计划每日更新一篇博客，今日2023-04-19，日更第三天，昨日更新：深度学习优化方法。