C/C++数据结构（九） —— 链式二叉树

---

前言

我们前面已经学习了 树 的基本概念，以及 二叉堆 的实现，那么今天我们将进行 二叉树 的基本操作。

1. 存储结构

顺序存储

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，也就是数组的下标要能体现结点之间的逻辑关系，比如双亲与孩子的关系，左右兄弟的关系等。

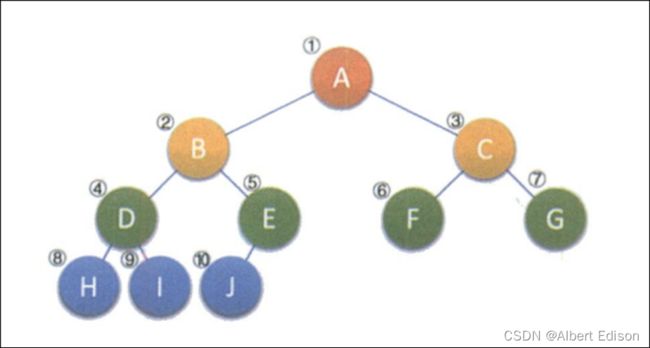
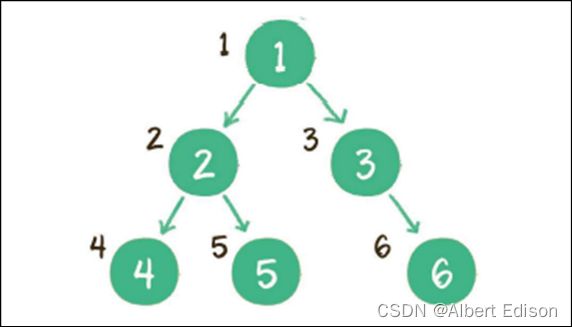
先来看看完全二叉树的顺序存储，一棵完全二叉树如下图所示。

将这棵二叉树存入数组中，相应的下标对应其同样的位置，如下图所示。

由于它定义的严格，所以用顺序结构也可以表现出二叉树的结构来。

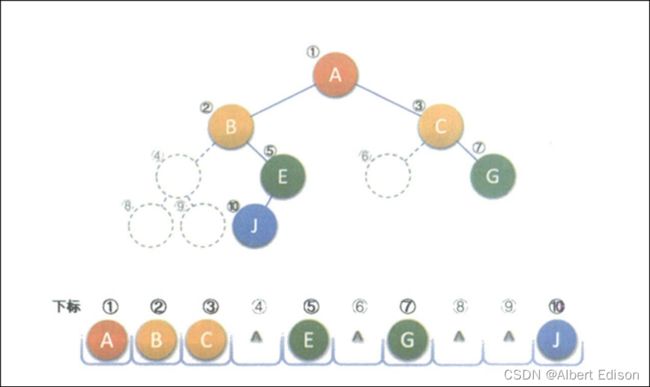
当然对于一般的二叉树，尽管层序编号不能反映逻辑关系，但是可以将其按完全二叉树编号，只不过，把不存在的结点设置为 “NULL” 而已。如下图，注意虚线结点表示不存在。

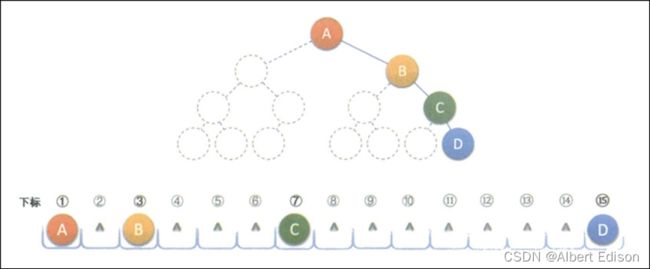
考虑一种极端的情况，一棵深度为 k 的右斜树，它只有 k 个结点，却需要分配 $2^k-1$ 个存储单元空间，这显然是对存储空间的浪费，例如下图所示。所以，顺序存储结构一般只用于完全二叉树。

链式存储

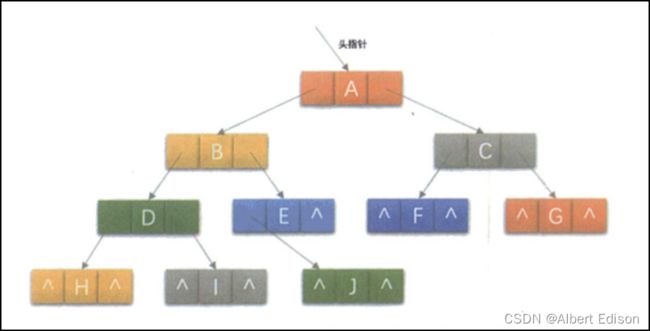
既然顺序存储适用性不强，我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域 是比较自然的想法，我们称这样的链表叫做二叉链表。

结点结构图如下表所示。

其中，data 是数据域；left 和 right 都是指针域，分别存放指向左孩子和右孩子的指针。

所以我们定义的二叉树链式结构的代码如下

typedef int BTDataType; //默认存储的是int类型的数据

//二叉树的链式节点结构定义
typedef struct BinaryTreeNode
{
	BTDataType data; //数据域
	struct BinaryTreeNode* left; //指向左孩子的指针
	struct BinaryTreeNode* right; //指向右孩子的指针
}BTNode;

逻辑图如下：

2. 构建一颗二叉树

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

代码示例：

typedef int BTDataType;

//二叉树的链式节点结构定义
typedef struct BinaryTreeNode
{
	BTDataType data; //数据域
	struct BinaryTreeNode* left; //指向左孩子的指针
	struct BinaryTreeNode* right; //指向右孩子的指针
}BTNode;

//创建一个节点
BTNode* BuyBTNode(BTDataType x) {
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL) {
		printf("malloc fail\n");
		exit(-1);
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

//构建一颗二叉树
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyBTNode(1);
	BTNode* node2 = BuyBTNode(2);
	BTNode* node3 = BuyBTNode(3);
	BTNode* node4 = BuyBTNode(4);
	BTNode* node5 = BuyBTNode(5);
	BTNode* node6 = BuyBTNode(6);

	//手动链接每个节点： 1->2->4->3->5->6
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	//根节点
	return node1;
}

再学习二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1）空树。
 
2）非空树：根节点，根节点的左子树、根节点的右子树组成的。
 

3. 二叉树的遍历

在计算机程序中，遍历本⾝是⼀个线性操作。所以遍历同样具有线性结构的数组或链表，是⼀件轻⽽易举的事情。

对于⼆叉树来说，是典型的⾮线性数据结构，遍历时需要把⾮线性关联的节点转化成⼀个线性的序列，以不同的⽅式来遍历，遍历出的序列顺序也不同

那么二叉树有那些遍历方式呢？

从节点之间位置关系的⾓度来看，⼆叉树的遍历分为 4 种：

1）前序遍历
 
2）中序遍历
 
3）后序遍历
 
4）层序遍历

从宏观的⾓度来看，⼆叉树的遍历归结为两⼤类：

1）深度优先遍历 （前序遍历、中序遍历、后序遍历）。
 
2）⼴度优先遍历 （层序遍历）。

4. 深度优先遍历

深度优先和⼴度优先这两个概念不⽌局限于⼆叉树，它们更是⼀种抽象的算法思想，决定了访问某些复杂数据结构的顺序。在访问树、图，或其他⼀些复杂数据结构时，这两个概念常常被使⽤到。

所谓深度优先，顾名思义，就是偏向于纵深，“⼀头扎到底” 的访问⽅式。可能这种说法有些抽象，下⾯就通过⼆叉树的前序遍历、中序遍历、后序遍历 ，来看⼀看深度优先是怎么回事吧。

前序遍历

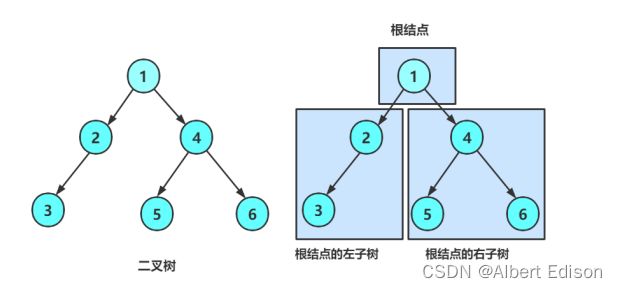
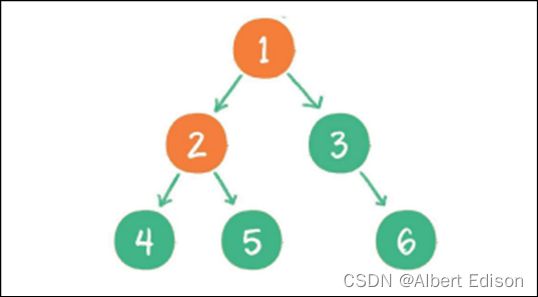
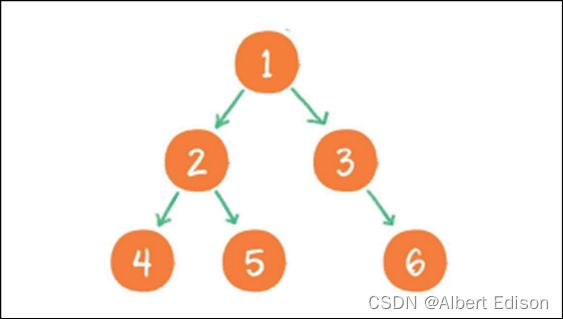
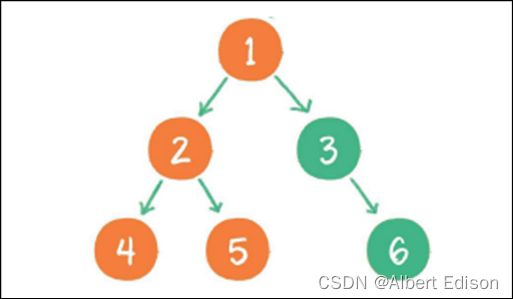
⼆叉树的前序遍历，输出顺序是：根节点、左⼦树、右⼦树。

规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

上图就是⼀个⼆叉树的前序遍历，每个节点左侧的序号代表该节点的输出顺序，详细步骤如下。

（1）首先输出的是根节点 1

（2）由于根节点 1 存在左孩子，输出左孩子节点 2

（3）由于节点 2 也存在左孩子，输出左孩子节点 4

（4）节点 4 既没有左孩子，也没有右孩子，那么回到节点 2，输出节点 2 的右孩子节点 5

（5） 节点 5 既没有左孩子，也没有右孩子，那么回到节点 1，输出节点 1 的右孩子节点 3

（6）节点 3 没有左孩子，但是有右孩子，因此输出节点 3 的右孩子节点 6

到此为止，所有的节点都遍历输出完毕。

代码示例

//前序遍历
void PrevOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL "); //可以把空节点也打印出来
		return;
	}
	
	//根 - 左子树 - 右子树
	printf("%d ", root->data); //显示节点数据
	PrevOrder(root->left); //先序遍历左子树
	PrevOrder(root->right); //先序遍历右子树
}

中序遍历

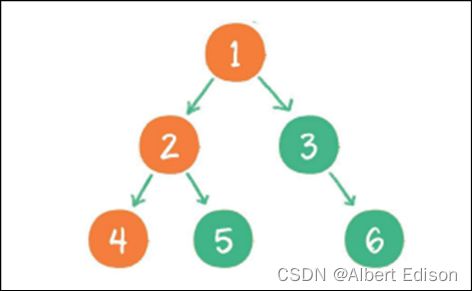
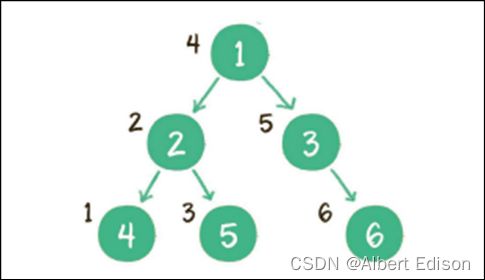
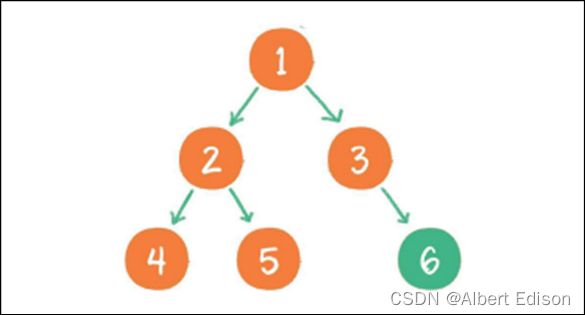
⼆叉树的中序遍历，输出顺序是：左⼦树、根节点、右⼦树。

规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。

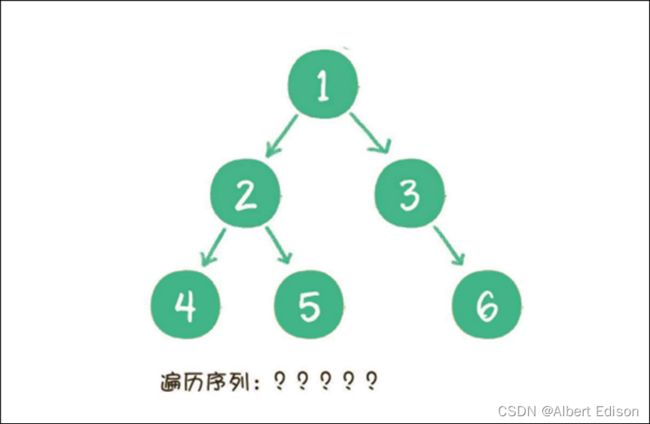
上图就是⼀个⼆叉树的中序遍历，每个节点左侧的序号代表该节点的输出顺序，详细步骤如下。

（1）⾸先访问根节点的左孩子，如果这个左孩子还拥有左孩子，则继续深⼊访问下去，⼀直找到不再有左孩子的节点，并输出该节点。显然，第⼀个没有左孩子的节点是节点 4

（2）依照中序遍历的次序，接下来输出节点 4 的父节点 2

（3）再输出节点 2 的右孩子节点 5

（4）以节点 2 为根的左⼦树已经输出完毕，这时再输出整个⼆叉树的根节点 1

（5） 由于节点 3 没有左孩子，所以直接输出根节点 1 的右孩子节点 3

（6） 最后输出节点 3 的右孩子节点 6

到此为止，所有的节点都遍历输出完毕。

代码示例

//中序遍历
void InOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	InOrder(root->left); //中序遍历左子树
	printf("%d ", root->data); //显示节点数据
	InOrder(root->right); //中序遍历右子树

}

后序遍历

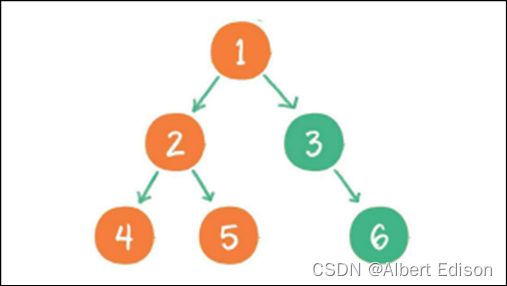
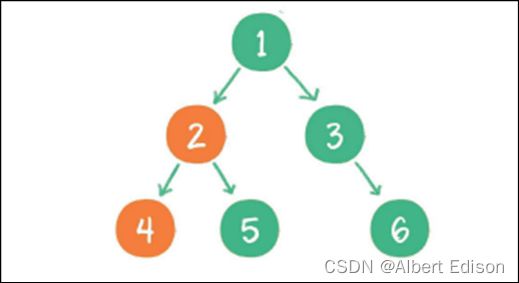
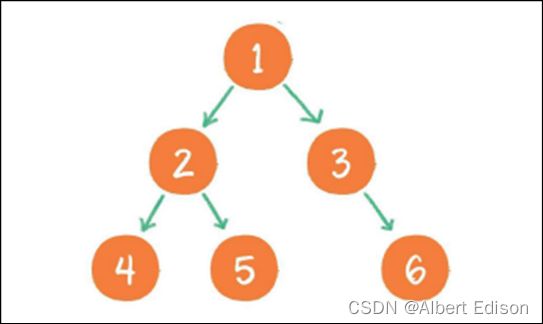
⼆叉树的后序遍历，输出顺序是：左子树、右子树、根节点。

规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点。

上图就是⼀个⼆叉树的后序遍历，每个节点左侧的序号代表该节点的输出顺序。

代码示例

//后序
void PostOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	PostOrder(root->left); //后序遍历左子树
	PostOrder(root->right); //后序遍历右子树
	printf("%d ", root->data); //显示节点数据
}

5. 广度优先遍历

如果说深度优先遍历是在一个方向上 “一头扎到底”，那么广度优先遍历则恰恰相反：先在各个方向上各走出 1 步，再在各个方向上走出第 2 步、第 3 步…一直到各个方向全部走完。

听起来有些抽象，下面让我们通过二叉树的层序遍历，来看一看广度优先是怎么回事。

层序遍历

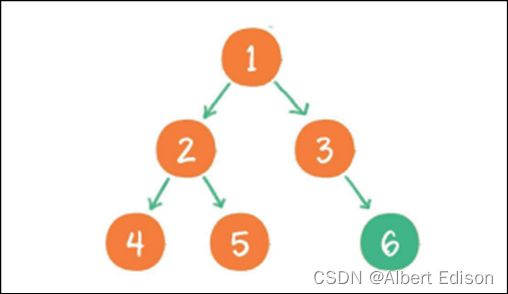
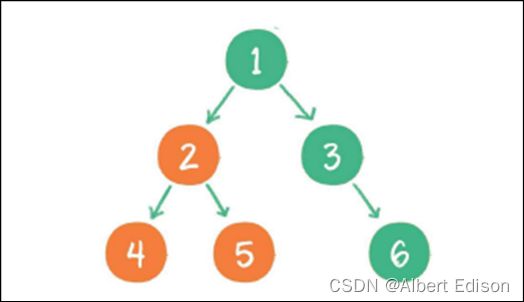
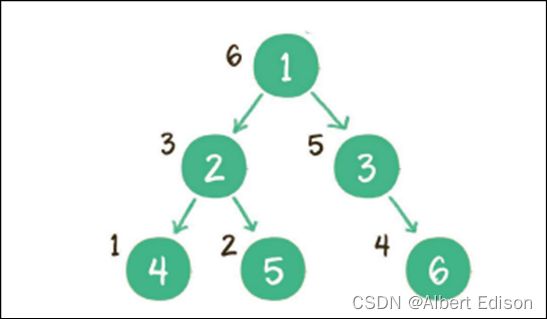
层序遍历，顾名思义，就是⼆叉树按照从根节点到叶⼦节点的层次关系，⼀层⼀层横向遍历各个节点。

规则是若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。

上图就是⼀个⼆叉树的层序遍历，每个节点左侧的序号代表该节点的输出顺序。

这里我们需要借助之前学过的一个数据结构 队列 来实现层序遍历。

1）先把根入队列，借助队列，先进先出的性质。
 
2）上一层的节点出的时候，带下一层的节点进去。
 
3）一直重复，直到队列为空。
 
先入根节点，此时队列里面是有一个节点的，判断队列不为空，把根节点的数据取出来，然后在把根节点的左孩子节点和右孩子入进去，依次循环。
 
注意：上一个节点出来以后，把它下面的左右节点带进去。

详细步骤如下：

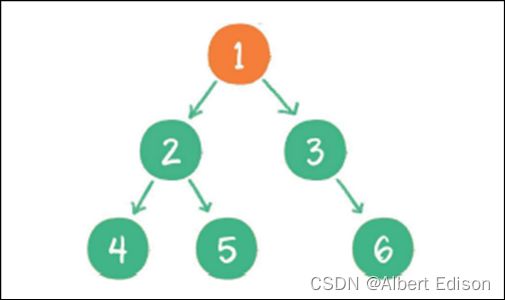
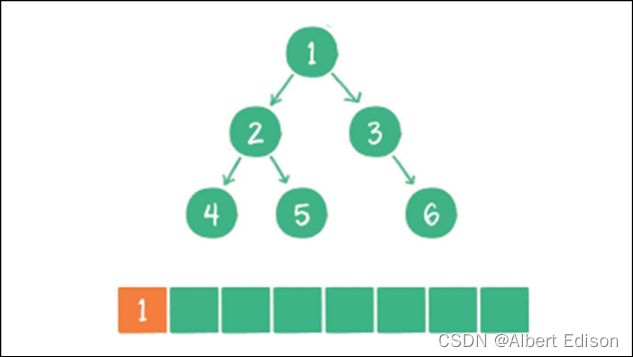
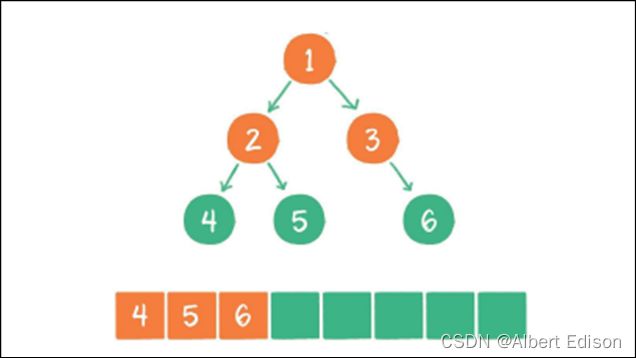
（1）根节点 1 进⼊队列

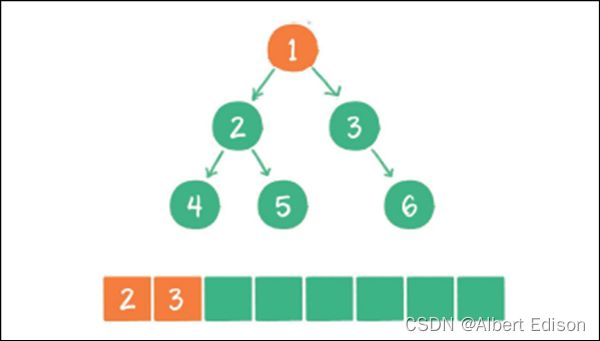
（2）节点 1 出队，输出节点 1，并得到节点 1 的左孩⼦节点 2、右孩⼦节点 3。让节点 2 和节点 3 ⼊队

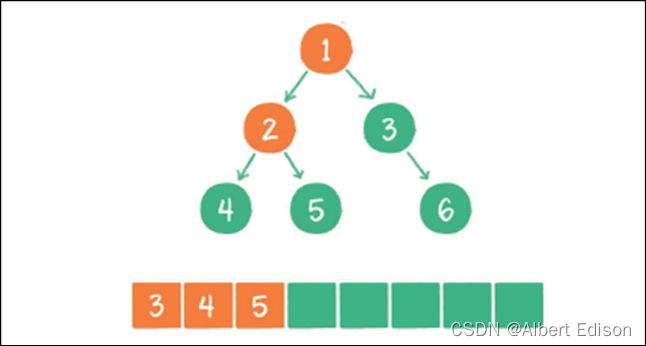
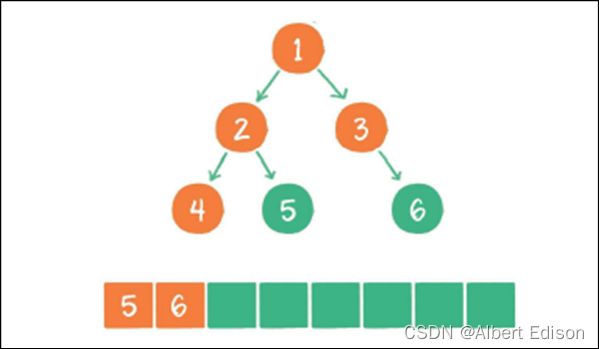
（3）节点 2 出队，输出节点 2，并得到节点 2 的左孩⼦节点 4、右孩⼦节点 5。让节点 4 和节点 5 ⼊队

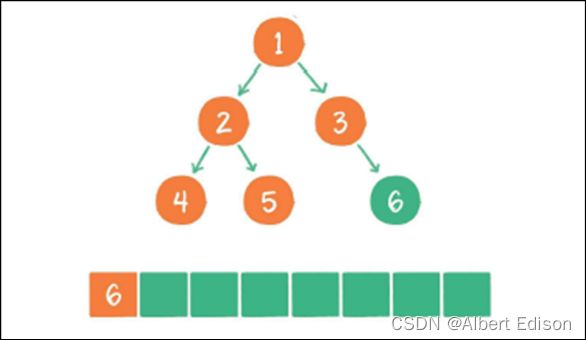
（4）节点 3 出队，输出节点 3，并得到节点 3 的右孩⼦节点 6。让节点 6 ⼊队

（5）节点 4 出队，输出节点 4，由于节点 4 没有孩⼦节点，所以没有新节点⼊队

（6）节点 5 出队，输出节点 5，由于节点 5 同样没有孩⼦节点，所以没有新节点⼊队

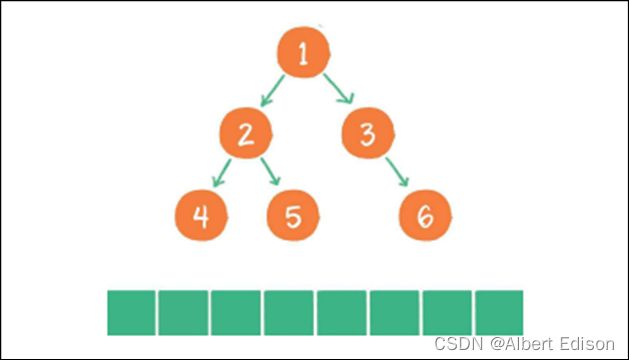
（7）节点 6 出队，输出节点 6，节点 6 没有孩⼦节点，没有新节点⼊队

到此为⽌，所有的节点都遍历输出完毕。

代码示例

//层序遍历
void LevelOrder(BTNode* root) {
	Queue q;
	QueueInit(&q);
	
	//队列不为空，入队列
	if (root) {
		QueuePush(&q, root);
	}

	//队列不为空,出队头的数据
	while (!QueueEmpty(&q)) {
		BTNode* front = QueueFront(&q); //取队头的数据
		QueuePop(&q); //然后Pop掉队列里面存的这个节点的指针

		printf("%d ", front->data); //然后访问data


		if (front->left) { //如果front的左子树不为空，那么就入队列
			QueuePush(&q, front->left);
		}

		if (front->right) { //如果front的右子树不为空，那么就入队列
			QueuePush(&q, front->right); 
		}
	}
}

6. 二叉树节点个数

我要求的是二叉树有值的结点的个数（空节点肯定不算）。

这里可以采用 分治思路， 把复杂的问题，分成更小规模的子问题，子问题再分成更小规模的子问题，直到子问题不可再分割，直接能出结果。

思路：

1）如果是空树，那么就返回 0。
 
2）如果不是空树，那么就等于：左子树节点个数+右子树节点个数+1（这个 1 就是自己）。

代码示例

//二叉树节点个数
int BTreeSize(BTNode* root) {
	return (root == NULL) ? (0) : (BTreeSize(root->left) + BTreeSize(root->right) + 1);
}

7. 二叉树叶子节点个数

所谓叶子节点，就是 没有任何 子节点 的节点称为叶子节点，也就是度为 0 的节点。

这里还是可以采用分治的思路：

1）若为空树，则叶子结点个数为 0。
 
2）若结点的左指针和右指针均为空，则叶子结点个数为 1（只剩一个根节点）。
 
3）除上述两种情况外，说明该树存在子树，其叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数。

代码示例

//二叉树叶子节点个数
int BTreeLeafSize(BTNode* root) {
	//1.只要我不是空，并且不是叶子，就会向下递归
	if (root == NULL) {
		return 0;
	}

	//2.如果我的左子树和右子树为空，那么我就是叶子节点
	if (root->left == NULL && root->right == NULL) {
		return 1;
	}

	//3.叶子结点的个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

8. 二叉树第 k 层节点个数

这里是求第 k 层的节点的个数，$k>=1$（k 从 1 开始的）

思路：

1）空树，返回 0。
 
2）不是空树，且 k==1，返回 1（求第一层的节点数，那么第一层只有一个根节点）。
 
3）不是空树，且 k>1，就转换成：左子树 k-1 层节点个数 + 右子树 k-1 层节点个数。

代码示例

//二叉树第 k 层节点个数
int BTreeKLevelSize(BTNode* root, int k) {
	assert(k >= 1);
	
	//空树，直接返回0
	if (root == NULL) {
		return 0;
	}
	
	//第一层节点个数
	if (root != NULL && k == 1) {
		return 1;
	}
	
	//相对于父结点的第k层的结点个数 = 相对于两个孩子结点的第k-1层的结点个数之和
	return BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1);
}

9. 二叉树查找值为 x 的节点

二叉树查找值为 x 的节点，然后返回节点的指针。

思路：

1）如果是空树，那么直接返回空。
 
2）先判断根节点的值是不是要查找的x，如果是，直接返回。
 
3）如果根节点不是，那么去左子树中查找。
 
4）如果左子树找不到，那么再去右子树中查找。

代码示例

//二叉树查找值为x的节点
BTNode* BTreeFind(BTNode* root, BTDataType x) {
	//如果根节点为空树，那么就直接返回空
	if (root == NULL) {
		return NULL;
	}

	//如果当前的data等于x，那么就返回当前节点指针
	if (root->data == x) {
		return root;
	}

	//如果当前节点不是，那么就去左边找，找到了就返回
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1) {
		return ret1;
	}

	//如果左边找不到，就去右边找，找到了就返回
	BTNode* ret2 = BTreeFind(root->right, x);
	if (ret2) {
		return ret2;
	}

	//如果左边和右边都没有找到，那么就返回空
	return NULL;
}

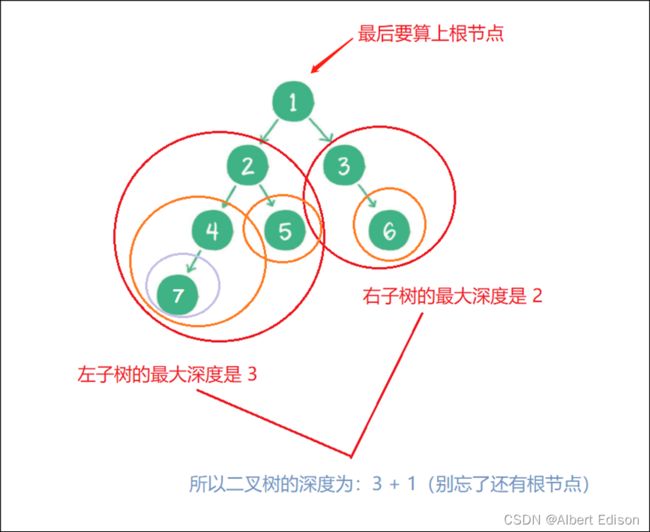
10. 二叉树的深度

求二叉树的深度，还是采用分治的思想：

1）若为空树，则深度为 0。
 
2）若不为空树，则深度 = 左右子树中深度最大的值 + 1（为什么要加1呢？因为还有第一层，也就是根节点这一层！）

如图所示：

代码示例

//二叉树的最大深度
int BTreeDepth(BTNode* root) {
	//空树高度为0
	if (root == NULL) {
		return 0;
	}
	
	//左子树的深度
	int leftDepth = BTreeDepth(root->left);
	
	//右子树的深度
	int rightDepth = BTreeDepth(root->right);
	
	//树的最大深度 = 左右子树中深度较大的值 + 1
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

11. 判断二叉树是否是完全二叉树

什么是完全二叉树？

前 n-1 层都是满的，最后一层不满，但是从左到右依次是连续的。

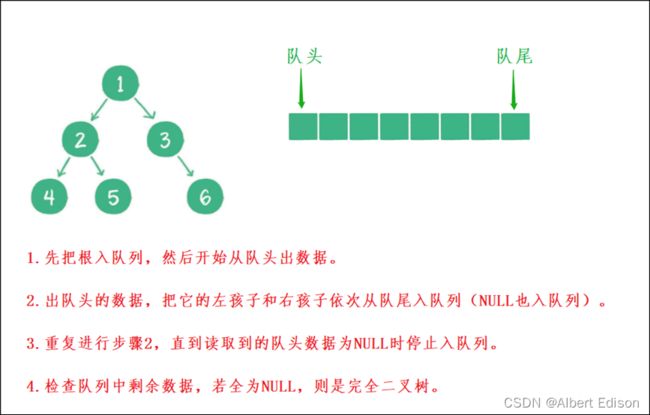
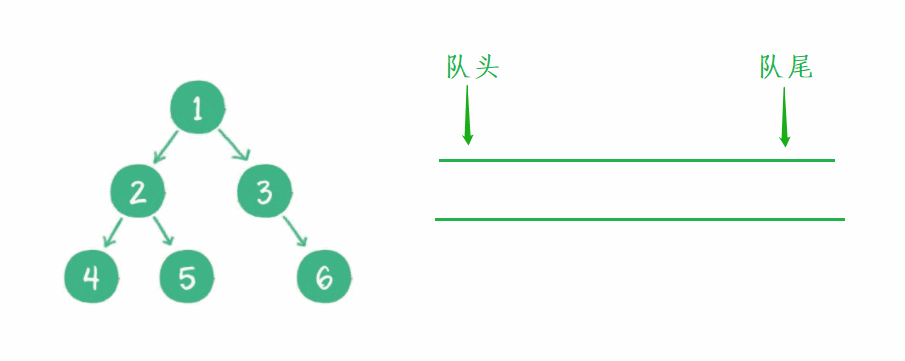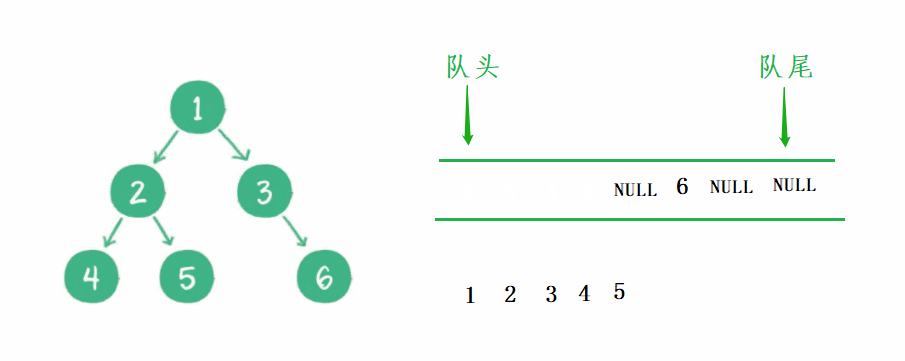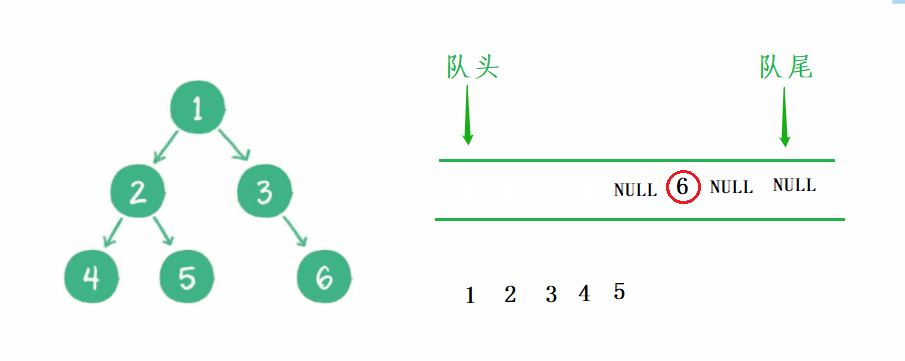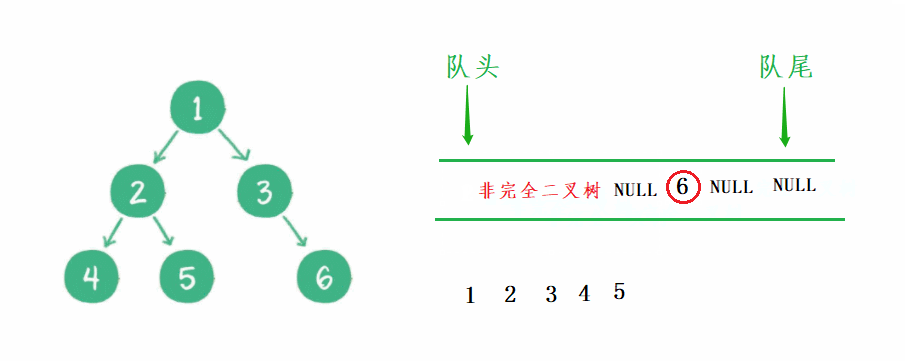
这里还是采用 队列 的思路：

1）层序遍历，空节点也进队列。
 
2）出到空节点以后，出队列中的所有数据，如果全是空，就是完全二叉树，如果有非空，就不是。

如图所示：

我这里用一个动图演示 非完全二叉树 的判断过程：

完全二叉树：非空节点都出完了，那么遇到空以后，队列后面肯定全是空。

代码示例

//判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root) {
	Queue q;
	QueueInit(&q);

	//队列不为空，入队列
	if (root) {
		QueuePush(&q, root);
	}

	//队列不为空,出队头的数据
	while (!QueueEmpty(&q)) {
		BTNode* front = QueueFront(&q); //取队头的数据
		QueuePop(&q);

		//如果出到空，那么就跳出循环，进入下一个循环，判断后面还有没有数据？
		if (front == NULL) {
			break;
		}
	
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}

	//出break以后，去判断
	while (!QueueEmpty(&q)) {
		BTNode* front = QueueFront(&q); //取队头的数据
		QueuePop(&q);

		//如果出到非空，那么说明不是完全二叉树
		if (front) {
			return false;
		}
	}

	//销毁队列
	QueueDestory(&q);
	return true;
}

12. 二叉树的销毁

二叉树需要注意销毁结点的顺序，遍历时我们选用后序遍历，也就是说，销毁顺序应该为：左子树、右子树、根。

我们必须先将左右子树销毁，最后再销毁根结点；若先销毁根结点，那么其左右子树就无法找到，也就无法销毁了。

代码示例

//二叉树销毁
void BTreeDestory(BTNode* root) {
	if (root == NULL) {
		return;
	}

	BTreeDestory(root->left); //先销毁左树
	BTreeDestory(root->right); //再销毁右树
	free(root); //释放根节点
}

总结

以上就是关于初阶二叉树的基本操作，那么这些的学习都是为了后面的二叉查找树、平衡二叉树、红黑树、B 树以及B+树打基础。

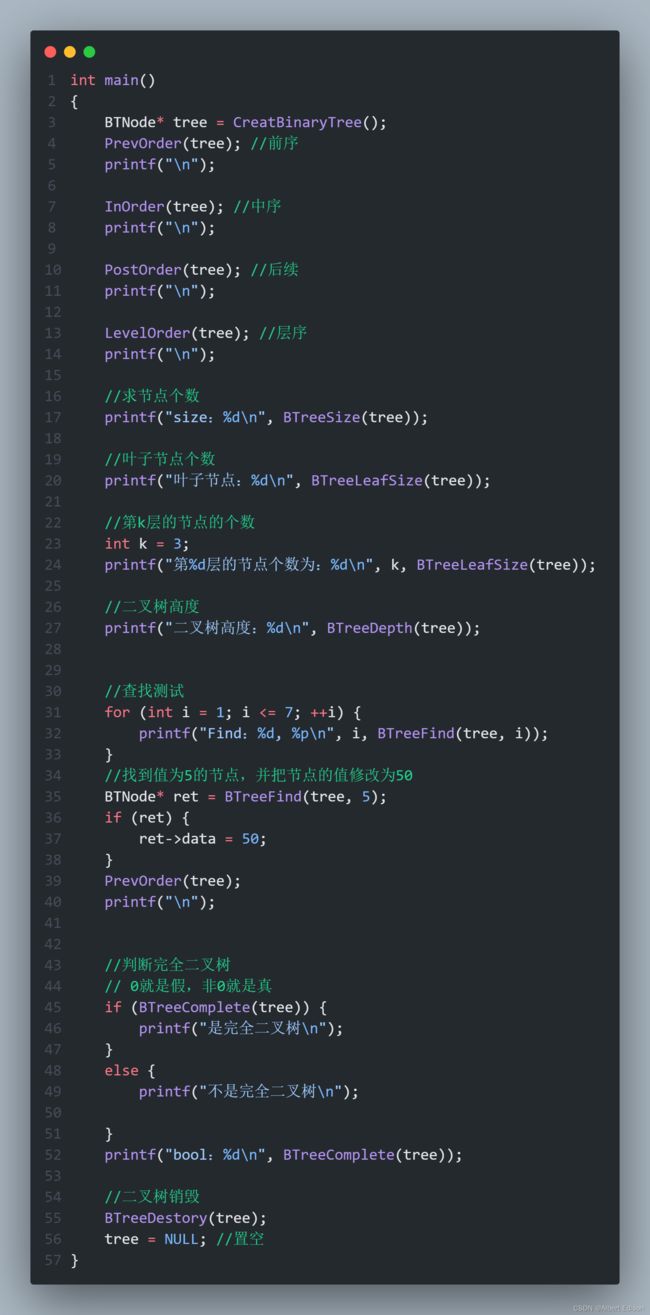
代码贴图

BinaryTree.c

Test.c