论文阅读笔记7——TransMOT: Spatial-Temporal Graph Transformer for MOT
论文:原文
没代码,离谱
被Graph transformer吸引,看看什么叫图transformer。
0.Abstract
TransMOT有效地对大数量的目标之间的关系进行了建模。它通过将已跟踪的目标作为稀疏带权图的集合来安排轨迹,并且构建一个空间的graph transformer的Encoder层,一个时域的graph transformer的Encoder层,一个空间的graph transformer的Decoder层。
为了提高精确度,提出了一个级联的关联结构,来处理低置信度的检测和长期遮挡。 但这个结构会消耗很大的计算资源。
在MOT15,16,17,20上都是SOTA。
\space
1.Introduction
在Introduction的开始,作者说了当前的基于Transformer的方法(引用的是TransTrack和TrackFormer)的缺陷:
1.一个视频包含了很多的目标。用Transformer对这些目标之间的关系进行时空建模是不太有效的,因为并没有将目标的时空结构纳入考虑。
2.要求比较大的计算资源和数据
3.不是SOTA
我不是很同意第一条。这些基于基本范式的Transformer的方法考虑到时空结构了。对于query-key机制,一般是一个query代表一个object,这些query作为transformer的输入,transformer是可以学习输入间的关系的,这考虑了空间结构。利用自回归的方式,这些query可以携带object的信息在帧间传输,这也考虑了时间结构。但是用graph的方式更直接,而已有的工作更含蓄。
对于第三点,不是SOTA问题也不大,我觉得,想法好就行了
\space
后面大概介绍了TransMOT的工作方式。
所有被跟踪的目标的轨迹都被弄成一系列稀疏的带权图,这些带权图是用目标的空间关系进行构建的,如下图所示:
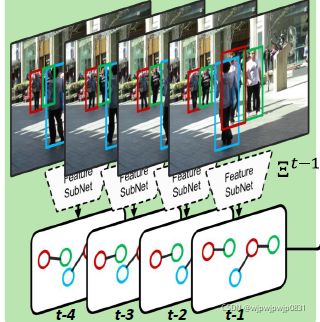
(如图,graph直接反映了目标在图片里的位置关系)
\space
基于这些稀疏图,TransMOT就建立了一个空间graph transformer Encoder,一个时域graph transformer Encoder,一个空间transformer decoder来建模。
由于图的稀疏性,计算起来更有效。
作者也建立了一个级联关联结构,来处理低置信度的检测和长时间遮挡。通过将TransMOT整合到这个级联关联结构中,不需要额外地学习关联的部分。
\space
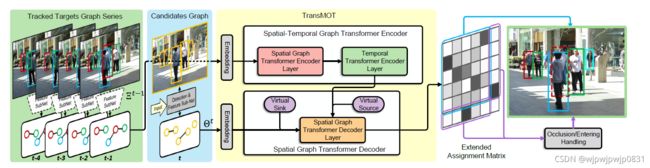
TransMOT整体结构如下图:
3.Overview
这部分大体介绍了TransMOT的工作方式。
在 t t t时刻,整个框架有 N t − 1 N_{t-1} Nt−1个tracklets,每个tracklet代表一个被追踪的目标。每个tracklet L i t − 1 \textbf{L}_i^{t-1} Lit−1维持一个状态的集合,比如说过去 T T T帧的位置 { x ^ t ′ i } t ′ = t − T t − 1 \{\hat{x}_{t'}^i\}_{t'=t-T}^{t-1} {x^t′i}t′=t−Tt−1外观特征 { f ^ t ′ i } t ′ = t − T t − 1 \{\hat{f}_{t'}^i\}_{t'=t-T}^{t-1} {f^t′i}t′=t−Tt−1.
现在有一个 t t t时刻的图像 I t I_t It,算法就估计退出界面的目标、决定哪个目标是被遮挡了的、计算现有目标的新位置 X ^ t = { x ^ i t } i = 1 N t \hat{\textbf{X}}_t=\{\hat{x}_{i}^t\}_{i=1}^{N_t} X^t={x^it}i=1Nt,并为新进入的目标创建tracklet。
\space
观察框架图,主要包含两部分,一是检测和特征提取的子网络,另一个就是时空graph transformer关联子网络。
这两个子网络的工作大体是:
- 在每一帧,检测和特征提取子网络(蓝色部分)产生 M t M_t Mt个候选检测目标建议,这个建议的集合记为 O t = { o j t } j = 1 M t \textbf{O}_t=\{o_j^t\}_{j=1}^{M_t} Ot={ojt}j=1Mt.这个网络也计算每个建议的外观特征。
- 时空graph transformer为每个tracklet找到最佳建议,并检测特殊事件,例如遮挡、退出、进入。
从这里看出来,TransMOT是将tracklet作为具体对象,有点类似于其他transformer方法中的query。
具体如何为买个tracklet找到最佳匹配呢?
将这个问题视作一个优化问题。设计一个affinity function,它用来估计 t − 1 t-1 t−1时刻的第 i i i个tracklet L i t − 1 \textbf{L}_i^{t-1} Lit−1和 t t t时刻建议候选中的 o j t o_j^t ojt的相似程度。
这实际上还是一个二部匹配问题,我们需要最小化一个cost。这个cost是所有匹配affinity的加权和,但我们希望权重以概率的形式来考虑,也就是对于一个 i i i,它属于 j j j的所有可能加起来应该是1。对于一个 j j j,也是同理。所以就有了下面的公式:
其中 A t = [ a i j t ] N t − 1 × M t A^t=[a_{ij}^t]_{N_{t-1}\times M_t} At=[aijt]Nt−1×Mt就代表了轨迹和候选的关联 (我认为也可以看成是affinity matrix)。
为了方便,将(1)(2)式改写为:
A t = Φ ( L t − 1 , O t ) A^t=\Phi(\mathcal{L}^{t-1},\mathcal{O}^t) At=Φ(Lt−1,Ot)
其中 L t − 1 \mathcal{L}^{t-1} Lt−1是 L i t − 1 \textbf{L}_i^{t-1} Lit−1的集合。
\space
为了进行时空建模,用稀疏带权图表示目标间的关系, 当前帧的图记为 Θ t \Theta^t Θt,之前 T T T帧的记为 E t − 1 = { ξ t − T , . . . , ξ t − 1 } E^{t-1}=\{\xi^{t-T},...,\xi^{t-1}\} Et−1={ξt−T,...,ξt−1}
(不知道为啥用不一样的字母)…
下面具体讲 Φ \Phi Φ是如何学习的,以及整个TransMOT具体是如何工作的。
\space
\space
4.TransMOT
为了学习出映射 Φ \Phi Φ进而计算出矩阵 A ‾ t \overline{A}^t At(Association的结果),作者用图中的橙色部分(两个Encoder,分别是时域Encoder和空间Encoder,和一个空间Decoder)来完成这个任务。
至于为什么用两个Encoder,作者在后文交代"可以更精确和有效地计算"。
下面对Encoders和decoder分别进行介绍。
\space
4.1 时域-空间的Graph Transformer Encoder
空间的graph Encoder是为了对轨迹之间的关系进行建模,时域的graph Encoder是为了进一步对轨迹间的时空信息进行混合和编码。
\space
4.1.1 空间Graph Transformer Encoder
观察框图,在 t t t时刻,过去 T T T帧的图的集合 E t − 1 = { ξ t − T , . . . , ξ t − 1 } E^{t-1}=\{\xi^{t-T},...,\xi^{t-1}\} Et−1={ξt−T,...,ξt−1}被输入到空间Encoder里。其中每个 ξ \xi ξ代表一个图,例如: ξ t − 1 = G ( x i t − 1 , E X t − 1 , ω X t − 1 ) \xi^{t-1}=G({x_i^{t-1}},E_X^{t-1},\omega_X^{t-1}) ξt−1=G(xit−1,EXt−1,ωXt−1)。其中 x , E , ω x,E,\omega x,E,ω分别表示顶点、边、权。
其中顶点的意义是第 i i i个轨迹的状态,应该和前面一样,指的是位置和外观。边的意义是两个轨迹间的空间关系,实际上就是用IoU来衡量的。 如果IoU大于0,就有边,否则就没有。权重的意义就是IoU的值。
因此权重矩阵 ω X t − 1 ∈ R N t − 1 × N t − 1 \omega_X^{t-1}\in\textbf{R}^{N_{t-1}\times N_{t-1}} ωXt−1∈RNt−1×Nt−1是一个稀疏矩阵。
\space
空间Encoder的工作流程如下:

\space
首先,输入图的集合 E t − 1 E^{t-1} Et−1,如图左侧所示,进行特征采集,得到特征张量 F s ∈ R N t − 1 × T × D \mathcal{F}_s\in\textbf{R}^{N_{t-1}\times T \times D} Fs∈RNt−1×T×D,其中 D D D是特征维度。实际上特征张量就保存了所有节点过去 T T T时刻的特征。每个节点的特征都经过一个线性层。
之后对输入的图进行自注意力计算,用多头图注意力(multi-head graph attention)机制,如下式:
其中 φ \varphi φ就是标准的scaled dot-product, i i i表示第i个head。 ∘ \circ ∘就是对应元素乘积。
这个式子的意义还有待理解。作者说:“它可以理解为独立地计算每个时间戳的空间图self-attention。”
多头注意力应该计算了目标间的关系,再与权重矩阵作用,确实也考虑了空间关系。但是“每个”时间戳是怎么来的?
\space
再看图右侧,作者采用了图卷积来对邻居节点的信息进行聚合。进行图卷积后,顶点特征的张量记为 F i V \mathcal{F}_i^V FiV 。和 F i A W \mathcal{F}_i^{AW} FiAW进行拼接 (?) ,再经过AddNorm,前馈网络等,得到最终的输出。
作者还说了一个图多头注意力权重特征张量,不知道这个量的意义在哪里,公式为:

意义就是先将多头的每个头得到的 F \mathcal{F} F做张量积再拼接,之后与 W O W^O WO做张量积。 W O W^O WO是什么也没交代。
\space
4.1.2 时域Graph Transformer Encoder
时域Encoder就比较简单了,它旨在在时间维度上独立地为每个tracklet使用标准Transformer 的Encoder层。所以在接受空间Encoder的输出后,首先将张量的前两个维度进行转置, 变为 F t m p e n ∈ R T × N t − 1 × D \mathcal{F}_{tmp}^{en} \in\textbf{R}^{T \times N_{t-1} \times D} Ftmpen∈RT×Nt−1×D.
它沿时间维度计算self-attention权重,并计算轨迹的时间注意加权特征张量。
\space
两个Encoder最后的输出记为 F o u t e n \mathcal{F}_{out}^{en} Fouten.
\space
4.2 空间的Graph Transformer Decoder

Encoders已经在时空上计算了过去 T T T帧轨迹间的联系,Decoder的作用就是基于Encoders的输出和当前帧的graph来做最终的预测。
Decoder接受两个输入,一是当前帧的graph Θ t = G ( { o j t } , E O t , ω O t ) \Theta^t=G(\{o_j^t\},E_O^t,\omega_O^t) Θt=G({ojt},EOt,ωOt),和前面一样,括号内分别是节点、边、权。二是Encoders输出的 F o u t e n \mathcal{F}_{out}^{en} Fouten.
构建当前帧graph的方式跟前面差不多,一个节点代表一个目标,IoU大于0的目标间才分配边,权值就是IoU值。
此外,还有一个添加虚拟节点(Virtual sink node) 的步骤。这个虚拟节点负责本帧当中退出的和遮挡的轨迹。这个虚拟节点和所有的节点相连,权值为0.5.
虚拟节点的做法和GNN中虚拟节点很像。虚拟节点也具有维度为 D D D的特征,是可学习的。
跟之前一样,仍旧吧节点的特征都汇聚起来。 由于加了一个虚拟节点,所以特征张量表示为 F t g t d e ∈ R ( M t + 1 ) × 1 × D \mathcal{F}_{tgt}^{de} \in\textbf{R}^{(M_{t}+1) \times 1\times D} Ftgtde∈R(Mt+1)×1×D。注意只有当前t时刻,因此时间维度是1.
这个张量经过图多头注意力,再Add&Norm后, 得到维度相同的输出 F a t t d e ∈ R ( M t + 1 ) × 1 × D \mathcal{F}_{att}^{de} \in\textbf{R}^{(M_{t}+1) \times 1\times D} Fattde∈R(Mt+1)×1×D
\space
对于从左边接收的 F o u t e n \mathcal{F}_{out}^{en} Fouten,为了应对本帧新出现的目标,所以加了一个虚拟源(Virtual source), 维度也是 D D D,是可学习的。这样就变成了 F o u t e n ′ ∈ R T × ( N t − 1 + 1 ) × D \mathcal{F}_{out}^{en'}\in\textbf{R}^{T \times (N_{t-1}+1)\times D} Fouten′∈RT×(Nt−1+1)×D.
作者说为什么只添加一个virtual source呢,因为发现添加多个和一个效果差不多。
为了将得到的两个张量融合,将 F a t t d e \mathcal{F}_{att}^{de} Fattde复制 ( N t − 1 + 1 ) (N_{t-1}+1) (Nt−1+1)次,得到 F a t t d e ′ ∈ R ( M t + 1 ) × ( N t − 1 + 1 ) × D \mathcal{F}_{att}^{de'}\in\textbf{R}^{(M_{t}+1) \times (N_{t-1}+1)\times D} Fattde′∈R(Mt+1)×(Nt−1+1)×D。
之后,将 F a t t d e ′ \mathcal{F}_{att}^{de'} Fattde′和 F o u t e n ′ \mathcal{F}_{out}^{en'} Fouten′再送入一个多头注意力机制,这时候就是交叉注意力了。得到输出,维度是 R ( M t + 1 ) × ( N t − 1 + 1 ) × D \textbf{R}^{(M_{t}+1) \times (N_{t-1}+1)\times D} R(Mt+1)×(Nt−1+1)×D.这个输出就反映了当前帧候选和已有轨迹的联系。
将输出经过线性层和softmax,把特征维度消掉,就得到了分配矩阵 A ‾ t ∈ R ( M t + 1 ) × ( N t − 1 + 1 ) \overline{A}^t\in \textbf{R}^{(M_{t}+1) \times (N_{t-1}+1)} At∈R(Mt+1)×(Nt−1+1)
\space
\space
4.3 Training
暂略。放宽了之前的约束条件,用类似于交叉熵的loss。
\space
4.4 级联数据关联框架
采用三阶段的数据关联。
第一阶段是对低置信度的候选进行匹配,用运动信息。
具体地,对于过去一定帧数都成功追踪的轨迹来说,用Kalman滤波去预测状态。将Kalman预测出的box和候选的box的IoU作为分数,然后用匈牙利算法去匹配。设定一个阈值,高于阈值就匹配,低于阈值就扔掉。
第二阶段是TransMOT计算剩余的轨迹和候选的拓展分配矩阵(为什么是剩余,有些低置信度的已经在第一阶段处理了。第一阶段处理的是简单的情况,所以也提高了速度)。就是用的二部匹配算法去做匹配。
第三个阶段是处理遮挡和重复。 对于连续T帧没有匹配的轨迹,用一种欧式的度量方式来重新匹配。
对于可能出现的重复检测,对于所有未匹配的候选,将其与所有关联对象匹配。还是计算bbox的重合程度。实际上应该是把重合程度高的删去了。
整个TransMOT的工作流程如下图所示:

\space
\space
5.Experiments
特征维度选1024,T选5. head数为8,用的普通的SGD,学习率0.0015.
感想:用的方法比较创新,结构也比较复杂。设计比较巧妙的地方是先用Kalman再用TransMOT,这样可以将简单情况先匹配,减少时间。文中数学表达很多,我觉得他是故意的。嗯。
没代码,没代码我知道你这瓜保熟吗(doge