2023.04.16 学习周报
文章目录
- 摘要
- 文献阅读
-
- 1.题目
- 2.摘要
- 3.简介
- 4.Dual-Stage Attention-Based RNN
-
- 4.1 问题定义
- 4.2 模型
-
- 4.2.1 Encoder with input attention
- 4.2.2 Decoder with temporal attention
- 4.2.3 Training procedure
- 5.实验
-
- 5.1 数据集
- 5.2 参数设置和评价指标
- 5.3 实验结果
- 6.结论
- MDS降维算法
- 梯度
-
- 1.基础知识
- 2.雅可比矩阵
- 3.海森矩阵
- 4.泰勒展开式
- 广义相对论
-
- 1.形象描述物体的位置
- 2.定义物体的速度
- 3.测地线方程
- 4.度规张量
- 5.黎曼曲率张量
- Navier-Stokes方程
-
- 1.NS方程的精髓
- 2.有限元法求解NS方程的步骤
- 3.加权残差法
- 总结
摘要
This week, I read a computer science about time series prediction. It is mentioned that few models can properly capture long-term temporal correlations and select relevant sequences for prediction. Therefore, it proposes a Dual-Stage Attention-Based Recurrent Neural Network to solve this problem. Firstly, an input attention mechanism is proposed, which can adaptively extract the features of each moment of the relevant node. Then, a temporal attention mechanism is used to select the implicit state of the relevant node across all time steps. The experimental results show that DA-RNN is superior to the most advanced time series prediction method. In addition, I learn MDS dimension reduction algorithm, gradient, general relativity and Navier-Stokes equations. For MDS dimension reduction algorithm, I try to use python to complete the algorithm implementation; For gradient, I learn Jacobian matrix and Hessian matrix to expand the understanding of gradient; For general relativity, I learn and comb the relevant knowledge; For NS equation, I learn Weighted Residual Method, which laid a foundation for learning Finite Element Method.
本周,我阅读了一篇与时间序列预测相关的文章。文章提到很少有模型可以适当地捕捉长期的时间相关性,并选择相关的序列进行预测。于是,文章提出了一种基于双阶段注意力的循环神经网络来解决这个问题。首先,提出了一个输入注意力机制,该机制可以自适应地提取相关节点每个时刻的特征。然后,使用了一个时间注意力机制,在所有时间步中选择相关节点的隐含状态。通过实验结果表明,DA-RNN 优于最先进的时间系列预测方法。此外,我学习了MDS降维算法、梯度、广义相对论和Navier-Stokes方程的相关内容。对于MDS降维算法,我尝试用python完成对算法的实现;对于梯度,我学习了雅可比矩阵和海森矩阵去扩展对梯度的认识;对于广义相对论,我学习并梳理了相关的知识;对于NS方程,我学习了加权残差法,为学习有限元法打下基础。
文献阅读
1.题目
文献链接:A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction
2.摘要
The Nonlinear autoregressive exogenous (NARX) model, which predicts the current value of a time series based upon its previous values as well as the current and past values of multiple driving (exogenous) series, has been studied for decades. Despite the fact that various NARX models have been developed, few of them can capture the long-term temporal dependencies appropriately and select the relevant driving series to make predictions. In this paper, we propose a dual-stage attention-based recurrent neural network (DA-RNN) to address these two issues. In the first stage, we introduce an input attention mechanism to adaptively extract relevant driving series (a.k.a., input features) at each time step by referring to the previous encoder hidden state. In the second stage, we use a temporal attention mechanism to select relevant encoder hidden states across all time steps. With this dual-stage attention scheme, our model can not only make predictions effectively, but can also be easily interpreted. Thorough empirical studies based upon the SML 2010 dataset and the NASDAQ 100 Stock dataset demonstrate that the DA-RNN can outperform state-of-the-art methods for time series prediction.
3.简介
背景:
1)时间序列预测算法已广泛应用于许多领域,如金融市场预测,天气预报,复杂动力系统分析等;
2)著名的自回归移动平均模型(ARMA)及其变体已经证明了它们在各种现实世界应用中的有效性,但它们不能建模非线性关系,也不能区分外生输入项;
3)为了解决这个问题,各种非线性自回归外生模型(NARX)已经被开发;
4)考虑最先进的 RNN 模型,例如编码器-解码器网络和基于注意力的编码器解码器网络,用于时间序列预测。
问题:
1)处理时间序列问题;
2)RNN 共享一组训练参数,因此梯度在反向传播过程中,不断连乘,数值不是越来越大,就是越来越小,即出现长序列训练过程中的梯度消失和梯度爆炸问题;
3)编码后的定长向量能力受到限制,无法存储众多时间步骤的信息,当序列长度增加时,性能将大幅下降。
亮点:
不仅在解码器的输入阶段引入注意力机制,还在编码器阶段引入注意力机制,编码器阶段的注意力机制实现了特征选取和把握时序依赖关系的作用。
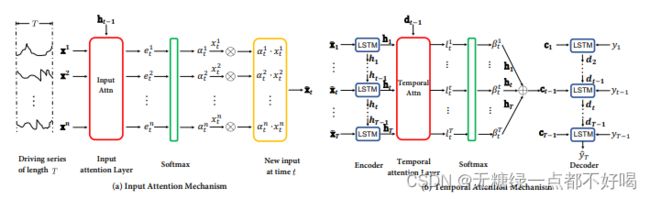
4.Dual-Stage Attention-Based RNN
针对目前非线性自回归模型难以捕捉长期时间依赖关系的问题,文章提出了基于双阶段注意力的循环神经网络(DA-RNN);第一步引入输入注意力机制去提取每个时间步的特征,第二步使用时间注意力机制去选择所有时间步长中相关的隐含状态;模型如下图所示:
4.1 问题定义
假定 n 维的时间序列表示为 X = (x^1, x^2, …, x^n)T = (x1, x2, …, xT) ∈ Rn*T,其中 T 表示序列长度。现给定一个目标序列 (y1, y2, …, yT-1) 以及其他序列 (x1, x2, …, xT) -> xt ∈ Rn,最终需要预测目标序列在 T 时刻的值,即学习得到一个映射函数F:

4.2 模型
4.2.1 Encoder with input attention
1)编码器采用 RNN 结构的 LSTM 模型,将每一个时间步的 n 维数据映射到 m 维,表示为:
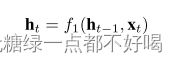
2)受到注意力机制的启发,提出input attention-based encoder,给定第k个序列 xk = (x1k, x2k, …, xTk)T ∈ RT,利用多层感知机构建注意力机制,表示为:
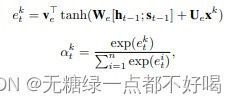
3)可以看出,首先在每一个单独的序列上计算 et^k,然后在不同的维度之间利用softmax计算 at^k,其表示第 k 个输入特征在时间 t 的重要性的注意力权重。因此,提取的序列特征以及每个时间步的隐含状态为:

4)模型使用输入注意力机制,编码器可以选择性地关注某些序列,而不是平等地对待所有序列。
4.2.2 Decoder with temporal attention
为了预测输出,使用基于 LSTM 的循环神经网络来作为编码输入信息的解码器;但是随着输入序列长度地增加,编码器-解码器网络的性能会迅速恶化;因此,在引入输入注意力的编码器后,在解码器中使用时间注意力机制来自适应地选择所有时间步长的相关编码器隐藏状态。
1)每个编码器隐藏状态在时刻 t 的注意力权重是根据前一个解码器隐藏状态 dt-1 和 LSTM 单元状态 s’t-1计算得到:
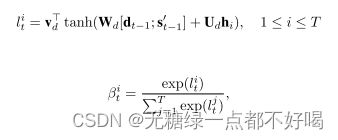
2)权重 βi,t 表示第 i 个编码器隐藏状态对t时刻值预测的重要性,即计算所有隐含状态的加权求和:

3) ct 在每个时刻是不一样的,然后与目标序列 (y1, y2, …, yT-1) 进行拼接,重新计算得到新的目标序列:
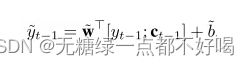
4)利用计算得到的 yt-1 hat,计算解码器在 t 时刻的隐含状态:
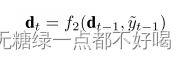
5)上图中 f2 是一个LSTM单元,最后估计预测输出 yT hat 为:
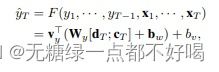
4.2.3 Training procedure
1)使用小批量随机梯度下降(SGD)和 Adam 优化器来训练模型;
2)minibatch 的大小是128,learning rate 从0.001开始,每 10000 次迭代后学习率降低10%;
3)DA-RNN 是光滑且可微的,因此参数可以通过均方误差作为目标函数的标准反向传播进行学习:

其中:N是训练样本的个数。
5.实验
5.1 数据集
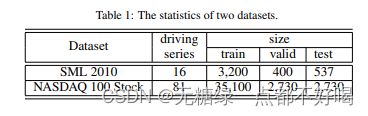
两个用于实证研究的数据集:
1)SML 2010 是一个用于室内温度预测的公共数据集;
2)NASDAQ 100 是一个用于股票预测的数据集。
5.2 参数设置和评价指标
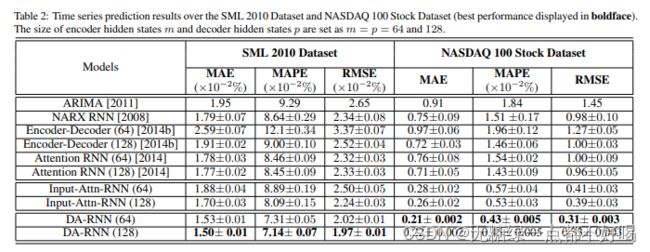
1)在 DA-RNN 中有三个参数,即窗口 T 的时间步长,编码器 m 的隐藏状态大小和解码器 p 的隐藏状态大小,其中分别设为 m = p = 64 和128。
2)为了衡量各种时间序列预测方法的有效性,考虑了三个不同的评估指标。
RMSE:

MAE:
![]()
MAPE:
![]()
5.3 实验结果
1)实验证明了输入注意力机制可以帮助 DA-RNN 选择相关的输入序列,抑制有噪声的输入序列:

2)实验证明了时间注意力机制可以在所有时间步中选择相关的编码器隐藏状态来捕获长期依赖关系:

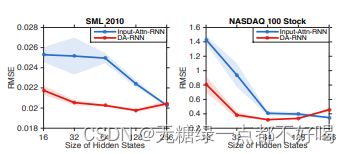
3)实验证明了 DA-RNN对参数的鲁棒性优于Input-Attn-RNN:
6.结论
1)作者提出了一种新型的基于注意力的双阶段循环神经网络(DA-RNN),该网络由具有输入注意力机制的编码器和具有时间注意力机制的解码器组成;
2)基于这两种注意力机制,DA-RNN 不仅可以自适应地选择最相关的输入特征,而且可以适当地捕获时间序列的长期时间依赖性;
3)作者提出的 DA-RNN 模型可用于时间序列预测,并有潜力作为计算机视觉任务中的通用特征学习工具;
4)在未来,作者将使用 DA-RNN 进行排序和二进制编码。
MDS降维算法
python实现MDS算法:
import numpy as np
from sklearn.datasets import load_iris
from sklearn.manifold import MDS
import matplotlib.pyplot as plt
# 1.计算两点间的距离
def cal_pairwise_dist(x):
sum_x = np.sum(np.square(x), 1)
dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)
return dist
# 2.MDS算法
def my_mds(data, n_dims):
n, d = data.shape
# 计算四个中间变量T1, T2, T3, T4
dist = cal_pairwise_dist(data)
dist[dist < 0] = 0
T1 = np.ones((n, n)) * np.sum(dist) / n ** 2
T2 = np.sum(dist, axis=1, keepdims=True) / n
T3 = np.sum(dist, axis=0, keepdims=True) / n
# 得到矩阵B
B = -(T1 - T2 - T3 + dist) / 2
# 对矩阵B进行特征分解
eig_val, eig_vector = np.linalg.eig(B)
index_ = np.argsort(-eig_val)[:n_dims]
picked_eig_val = eig_val[index_].real
picked_eig_vector = eig_vector[:, index_]
return picked_eig_vector * picked_eig_val ** 0.5
if __name__ == '__main__':
iris = load_iris()
data = iris.data
Y = iris.target
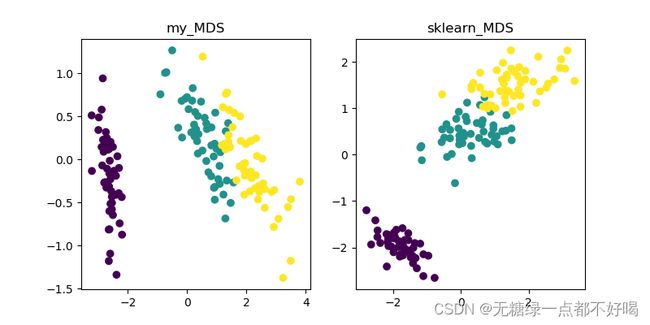
data_1 = my_mds(data, 2)
data_2 = MDS(n_components=2).fit_transform(data)
plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.title("my_MDS")
plt.scatter(data_1[:, 0], data_1[:, 1], c=Y)
plt.subplot(122)
plt.title("sklearn_MDS")
plt.scatter(data_2[:, 0], data_2[:, 1], c=Y)
plt.show()
梯度
1.基础知识
在空间中的每一个点都可以确定无限多个方向,一个多元函数在某个点也必然有无限多个方向。因此,在这无限多个方向中导数最大的一个是多少?它是沿什么方向达到的?描述这个最大方向导数及其所沿方向的矢量就是梯度,它直接反映了函数在这个点的变化率的数量级。因此,梯度的本质是一个矢量, 表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向变化最快,变化率最大。
雅可比矩阵和海森矩阵都和梯度相关,但是它们从不同的角度看待梯度。
2.雅可比矩阵
1)雅可比矩阵描述了相同维度的变量之间相互影响的程度;
2)假设 F:Rn → Rm 是一个从 n 维欧式空间映射到 m 维欧式空间的函数。这个函数由 m 个实函数组成:

如果这些函数的偏导数存在,则可以组成一个 m 行 n 列的矩阵,这个矩阵就是雅可比矩阵:
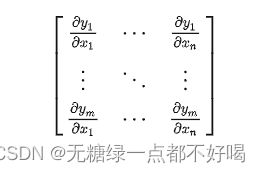
其中的每一个元素 Ji,j 对应的是 ∂yi/∂xj ,表示 xj 对 yi 的影响程度,可以表示为:
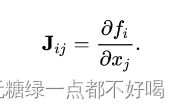
3)雅可比矩阵描述的是每个自变量变化时,函数值相应的变化情况,因此它是梯度的广度拓展;
4)我们可以发现雅可比矩阵不一定为方阵,它是一个有着矩阵外观的二阶张量;
5)梯度是雅可比矩阵的一种特殊形式,当 m=1 时函数的雅可比矩阵就是梯度。
3.海森矩阵
1)海森矩阵描述了梯度的变化率,即描述了函数曲面的弯曲程度和方向;
2)海森矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,假设有一个实数函数:

如果 f 的所有二阶偏导数都存在并在定义域内连续,那么函数 f 的海森矩阵为:

其中:第 i 行第 j 列的元素 Hi,j 表示函数曲面在 xi 和 xj 方向的弯曲程度。
3)因此,海森矩阵描述了梯度方向变化的程度,它是梯度的深度拓展。
综上所述,雅可比矩阵和海森矩阵从不同的角度描述了梯度的性质,前者描述了自变量变化对函数值的影响程度,后者描述了梯度在不同方向上的弯曲程度。这两个矩阵都是优化算法中的重要工具,可以用来决定梯度下降、牛顿法等优化算法的步长和方向。
4.泰勒展开式
1)n 阶泰勒展开式在 x = a 处展开:
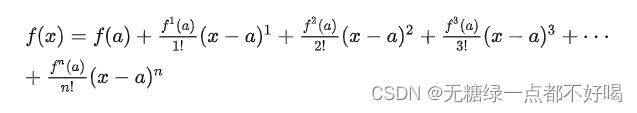
2)由泰勒展开式推导梯度下降:

因此,只需迭代 x 就可以让函数 f(x) 的值降低。
广义相对论
1.形象描述物体的位置
1)宇宙的时空具有四个维度,为了方便理解,我们把它简化为二维平面。在这个二维平面上画一条曲线去描述一个物体,这条曲线被称为物体的世界线。然后把这条世界线切分成多个具有相同间隙的线段,任选一个切点为原点,于是就可以对这些间隙进行编号,这样就把曲线转换成了一系列连续的点,这些就可以表示物体的轨迹,它代表了物体在时空中的运动。因此,这些编号被称为物体的原时τ。

2)为了表示物体在时空中的位置,于是在平面上建立一个二维坐标系,这个二维坐标系用网格表示,因此我们可以通过两个数字去表示物体的位置。需要注意的是,这些网格的形状和大小是不规则的,不具备任何物理意义。
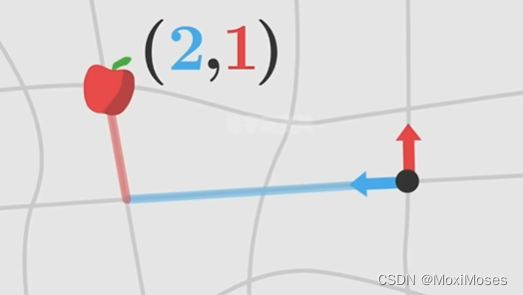
3)在真实的宇宙时空中,没有物体处于静止状态,尽管物体可以在空间中保持静止,但它仍会一直在时间的流逝中运动。当物体垂直地落向地面,我们可以准确地测量出物体到地心的距离,以及在测量物体下落时所花费的时间。因此,可以建立一个二维坐标系,横轴表示时间,纵轴表示物体的高度,随着原时的流逝,我们可以得到物体运动的轨迹。
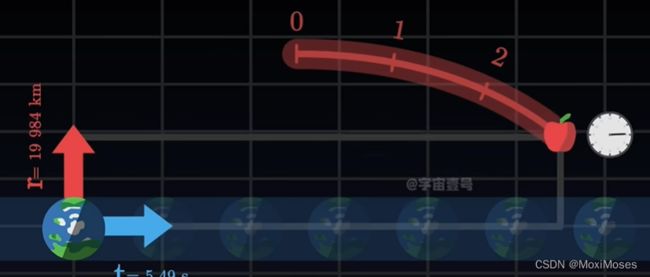
但需要注意的是,流逝的时间和物体的原时流逝速度不相同。
2.定义物体的速度
1)物体在时空中的速度是一个与世界线相切的向量,它的方向始终指向前方。物体的速度大小,即速率,在任何位置都是相同的。实际上,宇宙中所有物体都是以相同的速率在时空中运动,即光速c。因此可以得到第一个数学方程,宇宙中所有物体速度的大小始终等于光速:

2)考虑用坐标来表示物体的速度,在横轴和纵轴上分别有两个基向量,于是可以通过横轴和纵轴来分解速度。因此可以得到第二个数学方程,即速度等于各个维度速度分量的和,即爱因斯坦求和约定:

3)思考:在给定两个坐标值的前提下,是否可以通过勾股定理来求物体在时间线上的速度?其实是不可行的,因此两维平面上的坐标值不代表真实的物理距离,并且网格坐标是不规则的。
3.测地线方程
1)在宇宙中,物体在自然状态下会沿直线运动,当没有外力干扰时,物体在时空中的世界线趋向直线,即直线轨迹的平移对称性。因此,对于物体而言,我们用箭头表示物体的运动速度,就可以沿着箭头自身的平移来预测物体的运动,而这种平移速度形成的轨迹称为测地线。

2)在宇宙中,所有物体都倾向于沿着测地线运动,在侧地线上速度向量不会发生偏转,因此得到速度对原时的导数为0,于是把第二个方程带入到这个求导方程中并展开得到:

注意方程的左边,我们可以观察到速度分量随原时的变化以及基向量随原时的变化。
3)由于网格坐标系是不规则的,所以基向量是可以随着轨迹发生变化的,因此以纵轴方向上的基向量为例,它沿着世界线的变化可以被分解为沿着两个坐标维度的变化乘上物体的速率再求和,这是因为物体运动得越快,基向量变化得越快。
4)由此,我们可以用基向量对坐标维度的求导表示基向量是如何沿着坐标维度变化,于是得到的这个新向量可以用两个分向量Γ表示,而纵轴方向会有四个分向量Γ,因此对于整个二维平面会有8个Γ分向量,即克里斯托福弗符号。
5)克里斯托福弗符号表示网格如何沿着每个方向变化,将克里斯托福弗符号带入前面的方程中,就可以得到测地线方程,而我们可以通过测地线方程去预测物体的整个运动轨迹。

4.度规张量
1)由于网格坐标系的不规则性,因此无法提供坐标系中两点之间的真实距离以及夹角信息。
2)假设坐标系中有两个非常接近的点(在同一个网格中),考虑能否通过两个点抽象的坐标值反映两点间的真实距离?通常情况下,距离的平方总可以写成两条边所有可能的乘积组合再乘上系数,系数取决于网格的形状。于是,将这些系数放进两行两列的表格中,即度规张量g。

3)克里斯托福弗符号描述了基向量是如何随着网格变化,而基向量与网格的形状直接相关,网格的形状由度规张量表示。通过测量度规张量,就可以得到克里斯托福弗符号的具体数值。
4)度规张量只能计算近距离的两点距离,而对于远距离的两点距离,则需要沿着路径逐个计算度规张量,即 s = ∫ds。
5.黎曼曲率张量
1)实际上,时空不总是平坦的,它可以被弯曲,这会对物体的轨迹产生影响。例如,在一个平面上,有一个箭头,我们将它向上平移再向右平移或者向右平移再向上平移,会得到箭头的方向相同,但在一个球面上,有一个箭头,我们将它向上平移再向右平移或者向右平移再向上平移,会得到箭头的方向不相同,这表示表面的弯曲。
2)举例说明,在一个弯曲的平面上有一个基向量,经过上面两次不同的平移后,会得到两个方向不同的基向量,这两个基向量的差异用向量R表示,当其为0时,表示表面是平坦的。
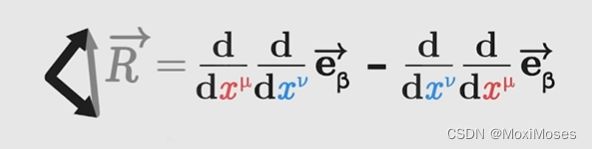
3)将克里斯托福弗符号带入上图公式,可得到向量R的最终表达式,并得到了分量的表示式,所有分量集合描述了沿表面平移基向量的每种可能性,即黎曼曲率张量(蕴含了一个表面在所有可能方向的曲率)。
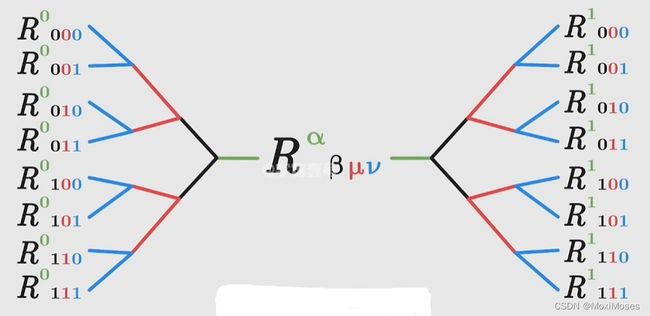
4)由于黎曼曲率张量的体量大,于是根据分量的数标将具有16个分量的黎曼曲率张量写成具有两行两列的里奇张量,而里奇张量描述了体积是如何沿着表面变化。
5)在球面上,两条平行测地线之间的体积随着我们在表面上前进而减少,而对于某些具有对称性的球面而言,它的曲率在所有方向上都是相同的,因此用数字R表示在所有方向上的平均曲率,即里奇标量。
Navier-Stokes方程
1.NS方程的精髓
1)NS方程是描述液体或气体运动行为的基本方程之一,可以用来解释热流、水流、空气流动等现象。
2)NS方程的主要含义是,液体或气体内部的每个微小元素都受到压力、摩擦力和重力的作用,从而产生推动力和阻力,进而引起流动运动。这些微小元素的运动状态可以用速度、压力和密度等参数来描述。
3)NS方程是偏微分方程,通常可以写成连续性方程和动量方程两个方程的形式。连续性方程描述了物质守恒,即质量在时间内的变化率等于质量流入减去质量流出。动量方程描述了运动守恒,即运动量在时间内的变化率等于运动量输入减去运动量输出,再考虑压力、摩擦力和重力的影响。
4)NS方程的精髓在于,它描述了流体作为一个整体的运动特性,涉及到许多微小元素的相互作用和运动状态。因此,对于实际应用中的流体流动问题,我们需要适当简化NS方程,并采用适当的边界条件和数值方法进行求解,以获得准确的结果。
2.有限元法求解NS方程的步骤
有限元法是一种求解偏微分方程的数值方法,其中NS方程是描述流体动力学的一类偏微分方程,可以用于分析流体的流动和行为。因此,使用FEM对NS方程进行求解,主要分为以下几个步骤:
1)建立几何模型:将流体区域离散化为有限数量的单元,形成一个计算网格。这些单元通常是三角形或四边形,具有良好的几何形状,并能够充分覆盖模型中的流体区域。
2)确定边界条件:在模型边界上指定流体的速度、温度、压力等边界条件,这些条件将影响NS方程的求解结果。
3)离散化NS方程:将NS方程离散为有限元方程组,这涉及将被求解变量分解成离散的节点,以及将偏微分方程转化成离散的代数方程。
4)求解节点位移:通过求解上述离散的代数方程组,确定每个节点的位移(速度和压力)。这些位移可以用于计算流体的速度场和压力场。
5)计算物理量:利用节点位移计算流体的物理量,如速度、压力、剪切应力等。
其中:在实际求解中,需要考虑如何选择单元类型、求解策略、网格剖分等方面的问题,以及如何确保数值稳定性和精度等问题。
3.加权残差法
问题:求解 x(t),使其满足微分方程 dx/dt + x = 0,初始条件为 x(0) = 1,求解区域 t ∈ [0, 1]。于是,得到这个方程的解析解是 e^-t。即:
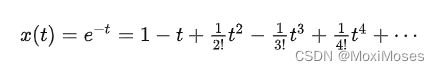
在计算机上展开到无穷阶,就能给出方程的精确解。但在现实中,只能考虑有限项,后面忽略的项称作截断误差。假设截断到二阶:
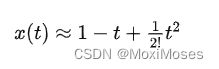
然后,代入原方程会产生残差 R,即 dx/dt + x = R,R ≠ 0,R 越接近于0,表示近似解越接近精确解。此时,我们可以明确知道精确解 e^-t 不在 (1, t, t^2 ) 这三个函数支撑起的函数空间中,于是我们可以做出改进。使用待定系数展开:
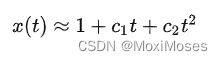
此时残差函数为:
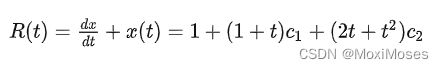
因此,通过调节 c1 和 c2,最小化 R(t) 的绝对值,就能得到比 1 - t + (1/2)*(t^2) 更好的解。
总结
本周,我用 python 实现 MDS 降维算法,根据上周的数学推导,实现起来难度不大并且代码简单易懂;对梯度的相关知识进行展开学习,试图去解释了为什么说雅可比矩阵是梯度的广度拓展,海森矩阵是梯度的深度扩展;整理学习了一些关于广义相对论的知识,对于里面的测地线方程、度规张量、黎曼曲率张量等,在下周会花时间学习并理解;加权残差法是有限元法的一个基础,而对于加权残差法,其最优情况是 R(t) 对任意 t 都等于零,但是这个做不到。因此,在下周我会学习四种不同的方法去减弱约束。