【程序员面试金典】面试题 02.07. 链表相交

题目描述

描述：给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

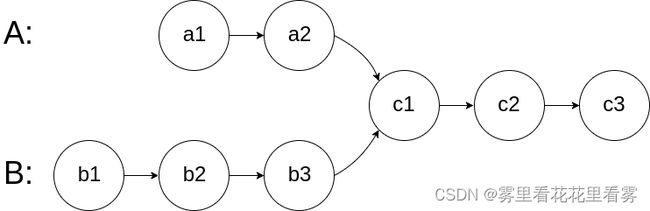
图示两个链表在节点 c1 开始相交：

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

listA 中节点数目为 m;
listB 中节点数目为 n;
0 <= m, n <= 3 * 104;
1 <= Node.val <= 105;
0 <= skipA <= m;
0 <= skipB <= n;
如果 listA 和 listB 没有交点，intersectVal 为 0;
如果 listA 和 listB 有交点，intersectVal == listA[skipA + 1] == listB[skipB + 1];

进阶：你能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案？

解题思路

思路1：最直观的想法是，计算两个链表的长度，然后较长长度的链表走两者长度之差步，接着两个链表一起走，走到相同即为相交处。

    int getLength(ListNode *head)
    {
        int num=0;
        while(head&&head->next)
        {
            num++;
            head=head->next;
        }
        return num;
    }
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* LA=new ListNode(0);
        LA->next=headA;
        ListNode* LB=new ListNode(0);
        LB->next=headB;
        int m=getLength(LA);
        cout<n)
        {
            while(diff>0&&p)
            {
                 p=p->next;
                 diff--;
            }
        }
        else if(m0&&q)
            {
                q=q->next;
                diff--;
            }
        }
        while(p&&q)
        {
            if(p->next==q->next)
            {
                return p->next;
            }
            p=p->next;
            q=q->next;
        }
        return NULL;
    }

思路2：假设p指向链表1的第一个节点，q指向链表2的第一个节点，并且使p和q一起走，当p结束则使p重新指向链表2的第一个节点，当q结束则使q重新指向链表1的第一个节点，当两者相等则是链表相交处。注意，p是指向p的下一个还是指向链表2的第一个节点是选择关系！q是指向q的下一个还是指向链表1的第一个节点也是选择关系！

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
   ListNode* p=headA;
   ListNode* q=headB;
   while(p!=q)
   {
       p=(p==NULL)?headB:p->next; //注意两者是选择关系
       q=(q==NULL)?headA:q->next; //注意两者是选择关系
   }
   return p; //相同点
}

总结：注意，思路2中，当p和q相等且为空，则表明没有相交喔！其中思路1的代码有点冗余喔！注意思路1中的创建头结点和不创建头结点的区别！