CRC校验
何为CRC
简介
CRC即循环冗余校验码(Cyclic Redundancy Check)是数据通信领域中最常用的一种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。
原理
CRC 算法的基本思想是将传输的数据[M(X)] 当做一个位数很长的数。将这个数除以另一个数[G(X)] ,得到的余数[R(X)] 作为校验数据附加到原数据后面,组成循环校验码。
M(X) 代表待编码的有效信息
G(X) 代表约定好的多项式
R(X) 代表代表检验位
由于,CRC的结构 = 信息位(N位) + 校验位(K位)
所以,CRC编码 = M(X) + R(X)
CRC编码方法
-
把待编码的N位有效信息位表示为多项式
M(X) -
把
M(X)左移K位,得到M(X)*X^K,这样就空出了K位,以便拼接K位余数,这里的K位是由多项式G(X)的最高位决定的 -
选取一个生成多项式
G(x),对M(X)*X^K做模二除 (多项式G(X)一般会直接给你,模二除看下面例子,实质是异或运算),以下是运算公式
( M(X) * X^K ) / G(X) = Q(X) + R(X) / G(X)
这里的Q(X)是商,它本身不重要,这里最重要的是求出余数R(X) -
将信息位
M(X)与余数R(X)拼接起来,构成CRC循环冗余校验码
CRC编码 = M(X) + R(X)
常见的校验
奇偶校验
为了解决数据传输过程中可能存在数据错误的问题,有人提出了一种比较简单的方式——奇偶校验法。
奇偶校验主要原理如下:
在原始数据流的头部或者末尾添加一位bit,此bit用于校验此数据包的正确与否。
例如
| 原始码 | 奇校验(奇数个1) | 偶校验(偶数个1) |
|---|---|---|
| 1011000 | 10110000 | 10110001 |
| 1010000 | 10100001 | 10100000 |
优缺点
奇偶校验法优点:
- 原理简单,实现方便。
奇偶校验法缺点:
- 奇偶校验的检错率只有50%,因为只有奇数个数据位发生变化能检测到,如果偶数个数据位发生变化,奇偶校验方式不能检测出错误。
- 奇偶校验每传输一个字节都需要加一位校验位,对传输效率影响很大。
- 奇偶校验只能发现错误,但不能纠正错误,也就是说它只能告诉你出错了,但不能告诉你怎么出错了,一旦发现错误,只好重发。
累加和校验
所谓的累加和校验有很多种,最常见的一种是在每次通信数据包最后都加一个字节的校验数据,这个校验字节里的数据是通信数据包里所有数据的不进位累加和。

比如下面的例子:
我们要传输的信息为: 6、23、4
加上校验和后的数据包:6、23、4、33
这里 33 为前三个字节的校验和。 接收方收到全部数据后对前三个数据进行同样的累加计算,如果累加和与最后一个字节相同的话就认为传输的数据没有错误。
累加和校验由于实现起来非常简单,也被广泛的采用。但是这种校验方式的检错能力也比较一般,对于单字节的校验和大概有1/256 的概率将原本是错误的通讯数据误判为正确数据。 之所以这里介绍这种校验,是因为CRC校验在传输数据的形式上与累加和校验是相同的,都可以表示为:通讯数据 校验字节(也可能是多个字节)
优缺点
- 实现起来方便简单,被广泛运用。
- 检错率一般,例如一个字节多1,一个字节少1,则会出现误判。
- 和奇偶校验一样,只能发现错误,但不能纠正错误。
海明码校验
你看得懂的海明码校验和纠错原理
CRC校验
模2除法
基于有限域GF(2)(即除以2的同余)的多项式环。
先说下什么是“模2除法”,我们知道模2加减是不进位、不借位的加减法,比如1+1=0,1+0=1,101+011=110,等于每一位的异或运算,相同bit加减为0,不同bit加减则为1。模2除法同理,即当部分余数首位是1时商取1,反之商取0。然后每一位的减法运算是按位减,不产生借位。余数的位数一定要是比除数位数只能少一位,哪怕前面位是0,甚至是全为0(附带好整除时)也都不能省略。举例如下图所示:
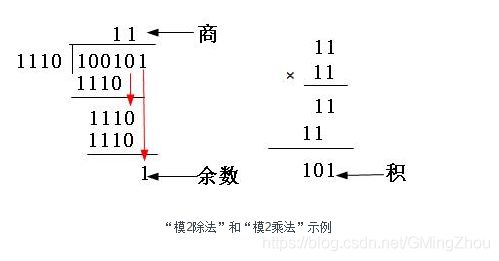
CRC校验码的计算示例
现假设选择的CRC生成多项式为G(X) = X4 + X3 + 1,要求出二进制序列10110011的CRC校验码。下面是具体的计算过程:
- 首先把生成多项式转换成二进制数,由G(X) = X4 + X3 + 1可以知道(,它一共是5位(总位数等于最高位的幂次加1,即4+1=5),然后根据多项式各项的含义(多项式只列出二进制值为1的位,也就是这个二进制的第4位、第3位、第0位的二进制均为1,其它位均为0)很快就可得到它的二进制比特串为11001。
- 因为生成多项式的位数为5,根据前面的介绍,得知CRC校验码的位数为4(校验码的位数比生成多项式的位数少1)。因为原数据帧10110011,在它后面再加4个0,得到101100110000,然后把这个数以“模2除法”方式除以生成多项式,得到的余数(即CRC码)为0100,如图5-10所示。注意参考前面介绍的“模2除法”运算法则。
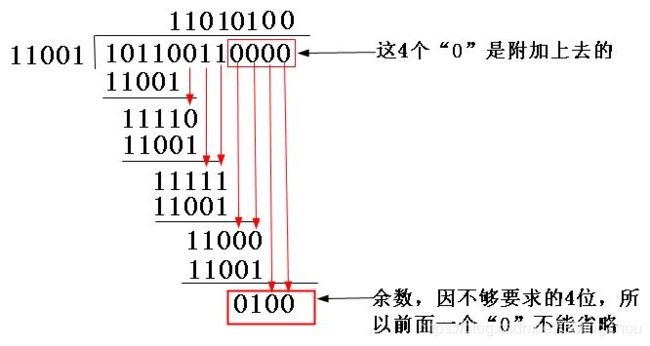
- 把上步计算得到的CRC校验0100替换原始帧101100110000后面的四个“0”,得到新帧101100110100。再把这个新帧发送到接收端。
- 当以上新帧到达接收端后,接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除,验证余数是否为0,如果为0,则证明该帧数据在传输过程中没有出现差错,否则出现了差错。
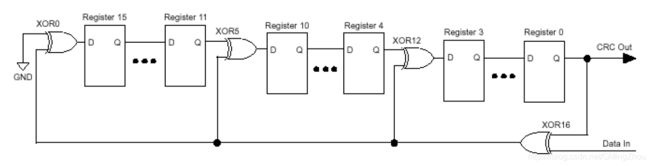
CRC校验电路原理图
常见CRC参数模型
| CRC算法名称 | 多项式公式 | 宽度 | 多项式 | 初始值 | 结果异或值 | 输入反转 | 输出反转 |
|---|---|---|---|---|---|---|---|
| CRC-4/ITU | x4 + x + 1 | 4 | 03 | 00 | 00 | true | true |
| CRC-5/EPC | x5 + x3 + 1 | 5 | 09 | 09 | 00 | false | false |
| CRC-5/ITU | x5 + x4 + x2 + 1 | 5 | 15 | 00 | 00 | true | true |
| CRC-5/USB | x5 + x2 + 1 | 5 | 05 | 1F | 1F | true | true |
| CRC-6/ITU | x6 + x + 1 | 6 | 03 | 00 | 00 | true | true |
| CRC-7/MMC | x7 + x3 + 1 | 7 | 09 | 00 | 00 | false | false |
| CRC-8 | x8 + x2 + x + 1 | 8 | 07 | 00 | 00 | false | false |
| CRC-8/ITU | x8 + x2 + x + 1 | 8 | 07 | 00 | 55 | false | false |
| CRC-8/ROHC | x8 + x2 + x + 1 | 8 | 07 | FF | 00 | true | true |
| CRC-8/MAXIM | x8 + x5 + x4 + 1 | 8 | 31 | 00 | 00 | true | true |
| CRC-16/IBM | x16 + x15 + x2 + 1 | 16 | 8005 | 0000 | 0000 | true | true |
| CRC-16/MAXIM | x16 + x15 + x2 + 1 | 16 | 8005 | 0000 | FFFF | true | true |
| CRC-16/USB | x16 + x15 + x2 + 1 | 16 | 8005 | FFFF | FFFF | true | true |
| CRC-16/MODBUS | x16 + x15 + x2 + 1 | 16 | 8005 | FFFF | 0000 | true | true |
| CRC-16/CCITT | x16 + x12 + x5 + 1 | 16 | 1021 | 0000 | 0000 | true | true |
| CRC-16/CCITT-FALSE | x16 + x12 + x5 + 1 | 16 | 1021 | FFFF | 0000 | false | false |
| CRC-16/X25 | x16 + x12 + x5 + 1 | 16 | 1021 | FFFF | FFFF | true | true |
| CRC-16/XMODEM | x16 + x12 + x5 + 1 | 16 | 1021 | 0000 | 0000 | false | false |
| CRC-16/DNP | x16 + x13 + x12 + x11 + x10 + x8 + x6 + x5 + x2 + 1 | 16 | 3D65 | 0000 | FFFF | true | true |
| CRC-32 | x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1 | 32 | 04C11DB7 | FFFFFFFF | FFFFFFFF | true | true |
| CRC-32/MPEG-2 | x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1 | 32 | 04C11DB7 | FFFFFFFF | 00000000 | false | false |
CRC算法参数模型解释
NAME:参数模型名称。
WIDTH:宽度,即CRC比特数。
POLY:生成项的简写,以16进制表示。例如:CRC-32即是0x04C11DB7,忽略了最高位的"1",即完整的生成项是0x104C11DB7。
INIT:这是算法开始时寄存器(crc)的初始化预置值,十六进制表示。
REFIN:待测数据的每个字节是否按位反转,True或False。
REFOUT:在计算后之后,异或输出之前,整个数据是否按位反转,True或False。
XOROUT:计算结果与此参数异或后得到最终的CRC值。
Java 实现参考
static int crc16tab[] = {
0x0000,0x1021,0x2042,0x3063,0x4084,0x50a5,0x60c6,0x70e7,
0x8108,0x9129,0xa14a,0xb16b,0xc18c,0xd1ad,0xe1ce,0xf1ef,
0x1231,0x0210,0x3273,0x2252,0x52b5,0x4294,0x72f7,0x62d6,
0x9339,0x8318,0xb37b,0xa35a,0xd3bd,0xc39c,0xf3ff,0xe3de,
0x2462,0x3443,0x0420,0x1401,0x64e6,0x74c7,0x44a4,0x5485,
0xa56a,0xb54b,0x8528,0x9509,0xe5ee,0xf5cf,0xc5ac,0xd58d,
0x3653,0x2672,0x1611,0x0630,0x76d7,0x66f6,0x5695,0x46b4,
0xb75b,0xa77a,0x9719,0x8738,0xf7df,0xe7fe,0xd79d,0xc7bc,
0x48c4,0x58e5,0x6886,0x78a7,0x0840,0x1861,0x2802,0x3823,
0xc9cc,0xd9ed,0xe98e,0xf9af,0x8948,0x9969,0xa90a,0xb92b,
0x5af5,0x4ad4,0x7ab7,0x6a96,0x1a71,0x0a50,0x3a33,0x2a12,
0xdbfd,0xcbdc,0xfbbf,0xeb9e,0x9b79,0x8b58,0xbb3b,0xab1a,
0x6ca6,0x7c87,0x4ce4,0x5cc5,0x2c22,0x3c03,0x0c60,0x1c41,
0xedae,0xfd8f,0xcdec,0xddcd,0xad2a,0xbd0b,0x8d68,0x9d49,
0x7e97,0x6eb6,0x5ed5,0x4ef4,0x3e13,0x2e32,0x1e51,0x0e70,
0xff9f,0xefbe,0xdfdd,0xcffc,0xbf1b,0xaf3a,0x9f59,0x8f78,
0x9188,0x81a9,0xb1ca,0xa1eb,0xd10c,0xc12d,0xf14e,0xe16f,
0x1080,0x00a1,0x30c2,0x20e3,0x5004,0x4025,0x7046,0x6067,
0x83b9,0x9398,0xa3fb,0xb3da,0xc33d,0xd31c,0xe37f,0xf35e,
0x02b1,0x1290,0x22f3,0x32d2,0x4235,0x5214,0x6277,0x7256,
0xb5ea,0xa5cb,0x95a8,0x8589,0xf56e,0xe54f,0xd52c,0xc50d,
0x34e2,0x24c3,0x14a0,0x0481,0x7466,0x6447,0x5424,0x4405,
0xa7db,0xb7fa,0x8799,0x97b8,0xe75f,0xf77e,0xc71d,0xd73c,
0x26d3,0x36f2,0x0691,0x16b0,0x6657,0x7676,0x4615,0x5634,
0xd94c,0xc96d,0xf90e,0xe92f,0x99c8,0x89e9,0xb98a,0xa9ab,
0x5844,0x4865,0x7806,0x6827,0x18c0,0x08e1,0x3882,0x28a3,
0xcb7d,0xdb5c,0xeb3f,0xfb1e,0x8bf9,0x9bd8,0xabbb,0xbb9a,
0x4a75,0x5a54,0x6a37,0x7a16,0x0af1,0x1ad0,0x2ab3,0x3a92,
0xfd2e,0xed0f,0xdd6c,0xcd4d,0xbdaa,0xad8b,0x9de8,0x8dc9,
0x7c26,0x6c07,0x5c64,0x4c45,0x3ca2,0x2c83,0x1ce0,0x0cc1,
0xef1f,0xff3e,0xcf5d,0xdf7c,0xaf9b,0xbfba,0x8fd9,0x9ff8,
0x6e17,0x7e36,0x4e55,0x5e74,0x2e93,0x3eb2,0x0ed1,0x1ef0
};
public static int crc16(String buf) {
int counter;
int crc = 0;
for (counter = 0; counter < buf.length(); counter++) {
int crcUnsign = (crc << 8) & 0xFFFF;
crc = crcUnsign ^ crc16tab[((crc >> 8) ^ (int) buf.charAt(counter)) & 0x00FF];
}
return crc;
}
public static int get(byte[] bytes) {
int[] table = {
0x0000, 0xC0C1, 0xC181, 0x0140, 0xC301, 0x03C0, 0x0280, 0xC241,
0xC601, 0x06C0, 0x0780, 0xC741, 0x0500, 0xC5C1, 0xC481, 0x0440,
0xCC01, 0x0CC0, 0x0D80, 0xCD41, 0x0F00, 0xCFC1, 0xCE81, 0x0E40,
0x0A00, 0xCAC1, 0xCB81, 0x0B40, 0xC901, 0x09C0, 0x0880, 0xC841,
0xD801, 0x18C0, 0x1980, 0xD941, 0x1B00, 0xDBC1, 0xDA81, 0x1A40,
0x1E00, 0xDEC1, 0xDF81, 0x1F40, 0xDD01, 0x1DC0, 0x1C80, 0xDC41,
0x1400, 0xD4C1, 0xD581, 0x1540, 0xD701, 0x17C0, 0x1680, 0xD641,
0xD201, 0x12C0, 0x1380, 0xD341, 0x1100, 0xD1C1, 0xD081, 0x1040,
0xF001, 0x30C0, 0x3180, 0xF141, 0x3300, 0xF3C1, 0xF281, 0x3240,
0x3600, 0xF6C1, 0xF781, 0x3740, 0xF501, 0x35C0, 0x3480, 0xF441,
0x3C00, 0xFCC1, 0xFD81, 0x3D40, 0xFF01, 0x3FC0, 0x3E80, 0xFE41,
0xFA01, 0x3AC0, 0x3B80, 0xFB41, 0x3900, 0xF9C1, 0xF881, 0x3840,
0x2800, 0xE8C1, 0xE981, 0x2940, 0xEB01, 0x2BC0, 0x2A80, 0xEA41,
0xEE01, 0x2EC0, 0x2F80, 0xEF41, 0x2D00, 0xEDC1, 0xEC81, 0x2C40,
0xE401, 0x24C0, 0x2580, 0xE541, 0x2700, 0xE7C1, 0xE681, 0x2640,
0x2200, 0xE2C1, 0xE381, 0x2340, 0xE101, 0x21C0, 0x2080, 0xE041,
0xA001, 0x60C0, 0x6180, 0xA141, 0x6300, 0xA3C1, 0xA281, 0x6240,
0x6600, 0xA6C1, 0xA781, 0x6740, 0xA501, 0x65C0, 0x6480, 0xA441,
0x6C00, 0xACC1, 0xAD81, 0x6D40, 0xAF01, 0x6FC0, 0x6E80, 0xAE41,
0xAA01, 0x6AC0, 0x6B80, 0xAB41, 0x6900, 0xA9C1, 0xA881, 0x6840,
0x7800, 0xB8C1, 0xB981, 0x7940, 0xBB01, 0x7BC0, 0x7A80, 0xBA41,
0xBE01, 0x7EC0, 0x7F80, 0xBF41, 0x7D00, 0xBDC1, 0xBC81, 0x7C40,
0xB401, 0x74C0, 0x7580, 0xB541, 0x7700, 0xB7C1, 0xB681, 0x7640,
0x7200, 0xB2C1, 0xB381, 0x7340, 0xB101, 0x71C0, 0x7080, 0xB041,
0x5000, 0x90C1, 0x9181, 0x5140, 0x9301, 0x53C0, 0x5280, 0x9241,
0x9601, 0x56C0, 0x5780, 0x9741, 0x5500, 0x95C1, 0x9481, 0x5440,
0x9C01, 0x5CC0, 0x5D80, 0x9D41, 0x5F00, 0x9FC1, 0x9E81, 0x5E40,
0x5A00, 0x9AC1, 0x9B81, 0x5B40, 0x9901, 0x59C0, 0x5880, 0x9841,
0x8801, 0x48C0, 0x4980, 0x8941, 0x4B00, 0x8BC1, 0x8A81, 0x4A40,
0x4E00, 0x8EC1, 0x8F81, 0x4F40, 0x8D01, 0x4DC0, 0x4C80, 0x8C41,
0x4400, 0x84C1, 0x8581, 0x4540, 0x8701, 0x47C0, 0x4680, 0x8641,
0x8201, 0x42C0, 0x4380, 0x8341, 0x4100, 0x81C1, 0x8081, 0x4040,
};
int crc = 0x0000;
for (byte b : bytes) {
crc = (crc >>> 8) ^ table[(crc ^ b) & 0xff];
}
return crc;
}
参考
- 最通俗的CRC校验原理剖析
- CRC校验原理及代码
- CRC(循环冗余校验)在线计算
- CRC检错技术原理
- 串口通信校验方式:奇偶校验、累加和校验
- 【基汤】关于CRC(循环冗余校验)