networkx 2-hop邻居(Ego graph)节点
1 Ego graph的简单介绍
自我网络(Ego graph)是一种特殊类型的网络,由一个中心节点和所有直接与之相连的其他节点组成。
中心节点被称为 自我(ego),而与之直接相连的其他周围节点被称为 分身( alters)。
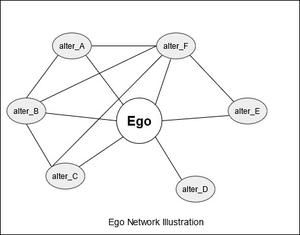
自我网络大多用于分析社会联系、链接和关系。下图所示的网络是自我网络的一个说明。中心节点(自我)显示为圆形,被邻近的节点(替代者)包围。
自我网络在社会网络分析中被广泛使用。关于自我网络的基本假设是,强关系是亲和性的。同源性是指在某种程度上有社会联系的个人显示出某些特质或相似性的倾向。简单地说,志同道合的人以某种方式紧密相连。自我网络帮助我们识别这些隐藏的联系。
可以下处理时经常会用到 Ego Network
- 信息的有效传播。
- 从链接中感知,例如 - 社会链接,关系。
- 获取资源,高效的连接路径生成。
- 社区检测,识别群体的形成。
- 分析社会支持的个人之间的联系。
2 networkx ego_graph api介绍
API介绍
ego_graph(G, n, radius=1, center=True, undirected=False, distance=None)
参数
- G (graph) : 一个 networkx构建的图
- n (node) : 单个节点,即要被计算的中心ego network node
- radius : 半径,以ego节点为圆心的半径,这个半径其实就是从ego节点出发的路径长度
- center (bool) : –是否包含ego 节点本身,默认是包含的,False为不包含
- undirected (bool) –默认为无向图,如果为 True则是有向图
- distance (key): 以边的什么属性作为距离度量,例如设置 distance=’weight’ 代表使用权重来作为 radius的距离度量。
3 实际构建
3.1 使用networkx 构建一个样本网络
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
G.add_edges_from([('A', 'B'), ('A', 'C'),('B', 'C'), ('E', 'F'),('D', 'E'), ('A', 'D'),('D', 'G'), ('C', 'F'),('D', 'F'), ('E', 'H')])
# Defining ego as large and red
# 定义 节点 A 作为 ego
ego = 'A'
pos = nx.spring_layout(G)
nx.draw(G, pos, node_color = "lavender",node_size = 800, with_labels = True)
options = {"node_size": 1200, "node_color": "r"}
nx.draw_networkx_nodes(G, pos, nodelist=[ego], **options)
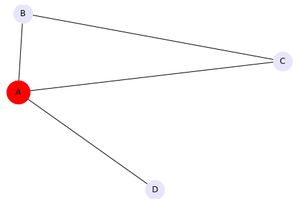
plt.show()3.2 在网络中单独抽取ego
这里的ego_graph 全部使用了默认参数,例如radius =1,默认是1-hop网络
hub_ego = nx.ego_graph(G, ego)
# 画出 ego 网络
nx.draw(hub_ego, pos, node_color="lavender",node_size = 800, with_labels = True)
nx.draw_networkx_nodes(hub_ego, pos, nodelist = [ego], **options)
plt.show()参考
Ego graph Using Networkx in Python - GeeksforGeeks
ego_graph — NetworkX 3.0 documentation