回归预测 | MATLAB实现GA-RF遗传算法优化随机森林的数据多输入单输出回归预测

回归预测 | MATLAB实现GA-RF遗传算法优化随机森林的数据多输入单输出回归预测

效果一览

基本介绍

1.Matlab实现GA-RF遗传算法优化随机森林多变量回归预测；
2.输入7个特征，输出1个，即多输入单输出；
3.运行环境Matlab2018及以上,运行主程序main即可，其余为函数文件无需运行，所有程序放在一个文件夹，data为数据集；
4.遗传算法优化随机森林树数目、最大深度，命令窗口输出RMSE、MAE、R2、MAPE等评价指标。

程序设计

• 完整程序和数据下载方式1(资源处直接下载)：MATLAB实现GA-RF遗传算法优化随机森林的数据多输入单输出回归预测
• 完整程序和数据下载方式2(订阅《RF随机森林》专栏，同时可阅读《RF随机森林》专栏收录的所有内容，数据订阅后私信我获取)：MATLAB实现GA-RF遗传算法优化随机森林的数据多输入单输出回归预测
• 完整程序和数据下载方式3(订阅《智能学习》专栏，同时获取《智能学习》专栏收录程序6份，数据订阅后私信我获取)：MATLAB实现GA-RF遗传算法优化随机森林的数据多输入单输出回归预测

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

%%  优化参数
dim    = 2;                         % 待优化的变量的个数
NIND   = 5;                         % 种群数目
MAXGEN = 10;                        % 最大迭代次数
PRECI  = 10;                        % 变量的二进制位数
GGAP   = 0.95;                      % 代沟
px     = 0.7;                       % 交叉概率
pm     = 0.01;                      % 变异概率
nu_min = [100,  1];                 % 参数范围最小值（决策树数目，最大深度） 
nu_max = [500, f_];                 % 参数范围最大值（最大深度小于特征数目） 

%%  种群初始化
trace = zeros(dim + 1, MAXGEN);      % 寻优结果的初始值
Chrom = crtbp(NIND, PRECI * dim);    % 初始种群
FieldD = [repmat(PRECI, 1, dim); ... % 区域描述器
    [nu_min; nu_max]; repmat([1; 0; 1; 1], 1, dim)];                       

%%  迭代优化
gen = 0;                                                        % 代计数器
pop = bs2rv(Chrom, FieldD);                                     % 计算初始种群的十进制转换
ObjV = Objfun(pop, p_train, t_train);                           % 计算目标函数值

while gen < MAXGEN
   FitnV = ranking(ObjV);                                       % 分配适应度值
   SelCh = select('sus', Chrom, FitnV, GGAP);                   % 选择
   SelCh = recombin('xovsp', SelCh, px);                        % 重组
   SelCh = mut(SelCh, pm);                                      % 变异
   pop = bs2rv(SelCh, FieldD);                                  % 子代个体的十进制转换
   ObjVSel = Objfun(pop, p_train, t_train);                     % 计算子代的目标函数值
   [Chrom, ObjV] = reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel);    % 重插入子代到父代，得到新种群
   pop = bs2rv(Chrom, FieldD);                                  % 解码种群
   gen = gen + 1;                                               % 代计数器增加

   % 获取每代的最优解及其序号,Y为最优解,I为个体的序号
   [Y, I] = min(ObjV);
   trace(1: dim, gen) = round(pop(I, :));                        % 记下每代的最优种群
   trace(end, gen) = Y;                                          % 记下每代的最优适应度
end

%%  获取最佳参数
max_tra(1) = trace(1, end);
max_tra(2) = trace(2, end);

%%  建立模型
model = regRF_train(p_train, t_train, max_tra(1), max_tra(2));

%%  仿真测试
t_sim1 = regRF_predict(p_train, model);
t_sim2 = regRF_predict(p_test , model);

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

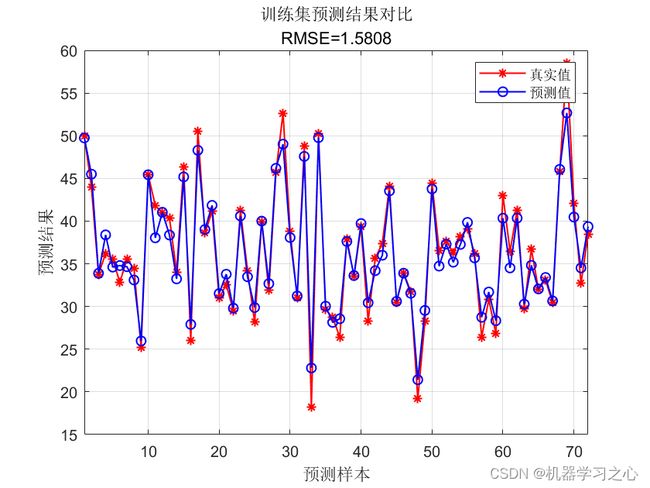
%%  均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
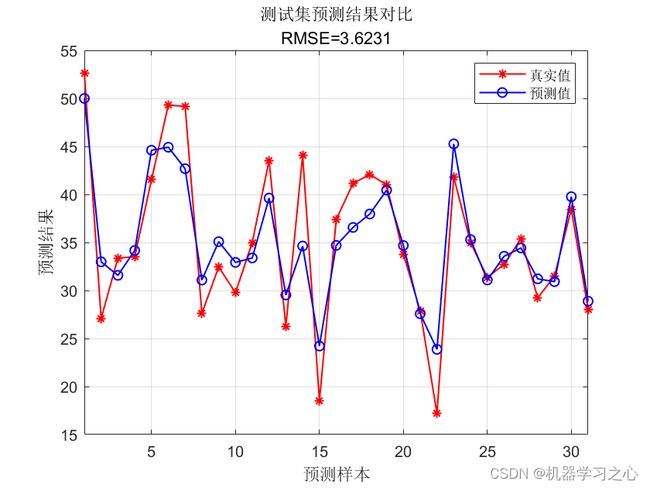
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);

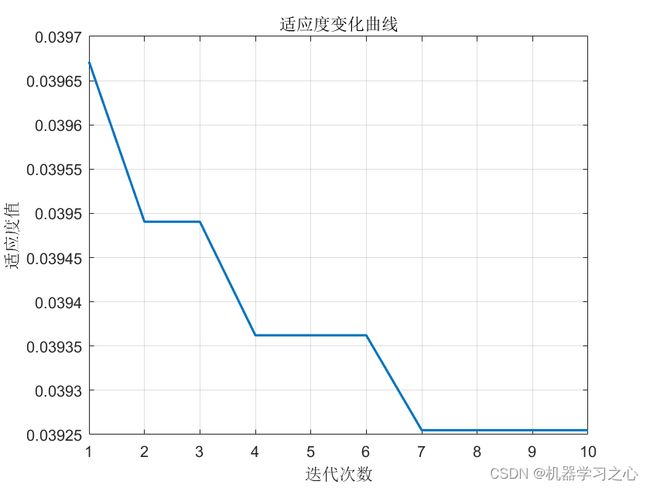
%%  优化迭代图
figure
plot(1: MAXGEN, trace(end, :), 'LineWidth', 1.5);
xlabel('迭代次数');
ylabel('适应度值');
string = {'适应度变化曲线'};
title(string)
grid on
%%  通用选择
% This function performs universal selection. The function handles
% multiple populations and calls the low level selection function
% for the actual selection process.

% Input parameters:
%    SEL_F     - Name of the selection function
%    Chrom     - Matrix containing the individuals (parents) of the current
%                population. Each row corresponds to one individual.
%    FitnV     - Column vector containing the fitness values of the
%                individuals in the population.
%    GGAP      - (optional) Rate of individuals to be selected
%                if omitted 1.0 is assumed
%    SUBPOP    - (optional) Number of subpopulations
%                if omitted 1 subpopulation is assumed
% Output parameters:
%    SelCh     - Matrix containing the selected individuals.

%%  检查参数一致性
if nargin < 3
    error('Not enough input parameter');
end

%%  确定种群规模 (Nind)
[NindCh, ~] = size(Chrom);
[NindF, VarF] = size(FitnV);

if NindCh ~= NindF
    error('Chrom and FitnV disagree');
end

if VarF ~= 1
    error('FitnV must be a column vector');
end
  
if nargin < 5
    SUBPOP = 1;
end

if nargin > 4
    if isempty(SUBPOP)
        SUBPOP = 1;
    elseif isnan(SUBPOP)
        SUBPOP = 1;
    elseif length(SUBPOP) ~= 1
        error('SUBPOP must be a scalar');
    end
end

if (NindCh / SUBPOP) ~= fix(NindCh / SUBPOP)
    error('Chrom and SUBPOP disagree');
end

%%  计算每个亚群的个体数量
Nind = NindCh / SUBPOP;

if nargin < 4
    GGAP = 1;
end

if nargin > 3
    if isempty(GGAP)
        GGAP = 1;
    elseif isnan(GGAP)
        GGAP = 1;
    elseif length(GGAP) ~= 1
        error('GGAP must be a scalar');
    elseif (GGAP < 0)
        error('GGAP must be a scalar bigger than 0');
    end
end

%%  计算新个体的数量（供选择）
NSel = max(floor(Nind * GGAP + 0.5), 2);

%%  从种群中选择个体
SelCh = [];
for irun = 1: SUBPOP
    FitnVSub = FitnV((irun - 1) * Nind + 1: irun * Nind);
    ChrIx = feval(SEL_F, FitnVSub, NSel) + (irun - 1) * Nind;
    SelCh = [SelCh; Chrom(ChrIx, :)];

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718