面试题思路分享以及延伸问题探讨三

---

1.前言

让我们紧接上文 单链表面试题分享二 ,这篇文章只给大家分享三道题.它们分别是:1.环形链表初阶 力扣141题-----2.环形链表进阶 力扣142题----- 3.复制带随机指针的链表 力扣138题 .值得注意的是这三道题的技巧性很强,是属于能想到方法实现起来很简单,想不到方法实现起来很复杂甚至不能实现的题.这里我提供给大家的思想和方法可能是我们之前出来没有遇见过也不好想到的方法,证明了这个地方我们已经开始上难度了,开始真正的在"玩"链表了.

---

---

---

2. 环形链表初阶

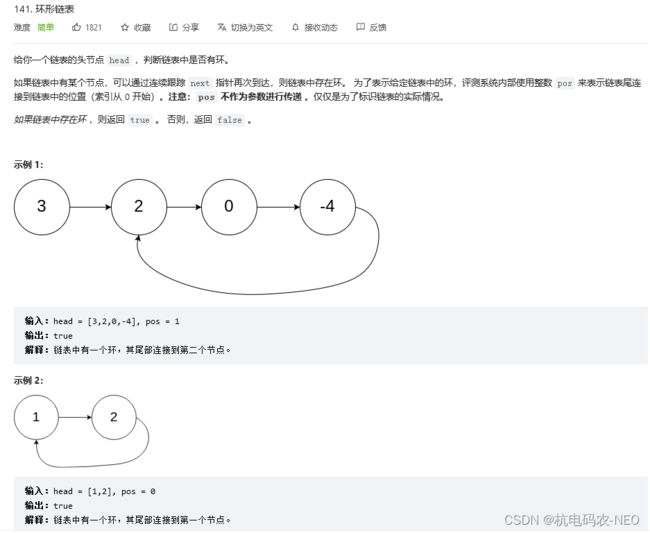
2.1 审题

先看题:

这个题我们不要去看它的pos之类的,容易误导我们的思维,这里的pos是是教我们自测输入的.这个题的意思就是,让我们判断一个链表是否存在环,如果如果就返回true,不存在返回false.当我们拿到这个题的时候会发现和别的链表题不同的是,如果链表存在环的话它是无法用NULL来作为我们循环结束的标志的,所以这个地方我们得另辟蹊径. 先给大家说结论,这个地方我们采用的方法叫做快慢指针法,顾名思义就是一个指针走得快一个指针走得慢, 我们通过画图来理解这个方法的第一步:

这个时候,fast刚好进入到我们的环中,如何进行我们的第二步, 那就是当slow指针也进入环时,这时fast指针在环中的某一个位置(不管slow指针进环前fast走了一圈还是多圈),这时我们设置slow和fast的距离(也就是它们两个之间的节点数)为N ,然后我们再来画图理解:

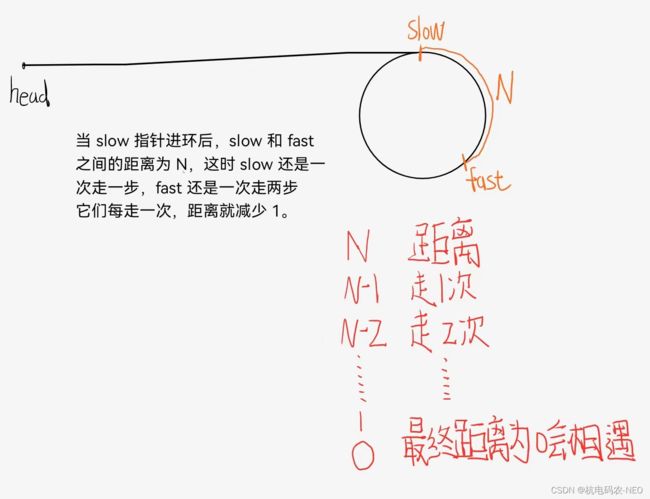因为它们两个指针每走一次距离减少1,所以它们永远不会错过,只要有环存在,它们就会相遇.下面我们来实现一下代码:

---

---

2.2 代码实现以及紧急情况的处理方法

bool hasCycle(struct ListNode *head) 
{
  struct ListNode* slow = head, *fast = head;
  while(fast&&fast->next)//fast和fast->next都不为空
  {
      slow=slow->next;
      fast=fast->next->next;
      if(slow==fast)
      {
          return true;
      }
  }
  return false;//如果fast或者fast->next为空证明链表中没有环
}

代码实现是很简单的,但是我们的思路是比较难想到的, 如果我们在参加面试或者比赛的时候遇见了这种题没有思路,时间也快不够了的时候,我们可以试着用题目给的条件来让代码通过(平时训练不建议这样做)

bool hasCycle(struct ListNode *head) 
{
    struct ListNode* cur=head;
    int count=0;
    while(cur)//遍历链表
    {
        cur=cur->next;
        count++;//题目说节点数小于10000
        if(count>10000)//所以当遍历到10000遍时一定为环,就返回true
        {
            return true;
        }
    }
    return false;
}

2.3 延伸问题

其实我们会发现,这个题考验的其实是我们的算法能力和思维能力,并不是在考我们的代码水平,所以这个地方的追加问题经常出现在面试时面试官的提问中,他第一步会问你这个题目的思路是怎么样的,他并不会让你去写代码,而是在你回答了你的思路后继续追加问你问题:比如:1.为什么为什么slow和fast一定会在环中相遇?它们会不会在环中错过,永远遇不上?请证明一下-----2.为什么slow走一步fast走两步,fast能不能走3步?4步?甚至n步?走n步还能不能遇上?请证明一下 这里我们就来探讨一下:

---

2.3.1 为什么slow和fast一定会遇上?

根据我们前面的推断其实我们已经有了一定认识,那就是当slow走一步,fast走两步的时候它们一定会遇上!
因为我们知道,fast一定是比slow先进入到环中的,所以当slow进入环之后,我们的fast肯定已经在环中走了某段距离并且停留在某个点上了.这时slow和fast的距离为N,每走一次,N的值就会减一,所以说我们的N不会出现跳过0的这种情况,N一定会在某次slow和fast走后变为0,这时就代表slow和fast相遇了.

---

2.3.2 走n步会是什么样的情况?

这里我们由易到难,先讨论slow走一步,fast走三步的情况:还是和之前一样,当slow进环后,我们令fast和slow的距离为N,目前这种情况它们俩走一次,N的值会减少二,那么我们说什么情况下N能够顺利的减到0呢?很明显那就是当N为2的倍数的时候(也就是N为偶数的时候)

---

我们会发现当N为偶数的时候我们能够顺利的将N减到0,也就是让slow和fast相遇,但是当N为奇数时,减到1的时候再减去2会得到-1,也就是fast直接越过了slow.那么当它们走了一圈没有相遇的时候它们后面还会相遇吗?我们画图来探讨一下:

---

可以看见如果第一圈没有追到不代表永远追不到,当N为奇数时,追完一圈fast在slow后面一个,所以它们的距离N’就变成了环的长度减一,这里把它们的距离又看作N’,即N’为偶数可以追上,N’为奇数就永远追不上了,因为当N’为奇数时相当于又重复了我们的第一遍操作. 当我们了解了走三步的情况,接下来我们来探讨slow走一步,fast走四步的情况:也就是slow和fast每走一次,它们的距离N就减少3,这里有了我们前面的经验很容易想到,如果N为3的倍数,那么N就可以减到0,也就是slow和fast可以相遇.当N不为3的倍数这个地方我们又要来判断一下:

---

当N不是3的倍数时有两种情况,就是最后一次走后,N为-1或者-2;也就是slow和fast的距离变成了环的长度减一或者环的长度减二.后面走N步就依此类推了.综上所述:这个题用slow走一步,fast走两步是最好的

---

---

---

3. 环形链表进阶

3.1 审题

先看题:

---

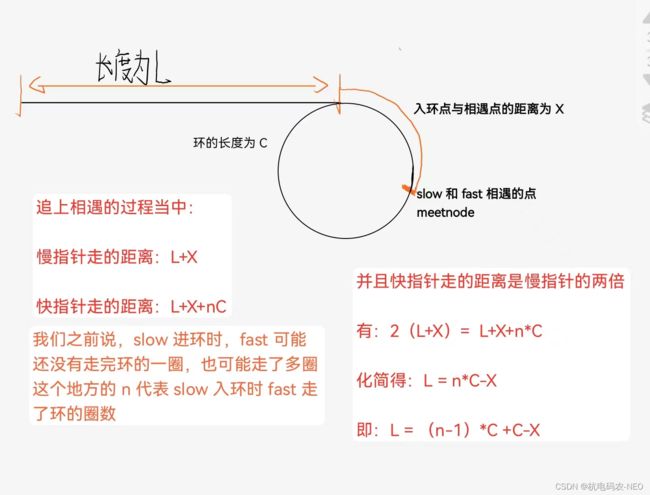
这个题相较于我们上一个题多了一个步骤,就是要返回链表开始入环的第一个节点.这个地方我们还是先用快慢指针来判断是否有环,slow走一步,fast走两步,当我们判断了链表有环之后,下一步应该怎么做?我们之前说这个地方的题技巧性很强,方法一般很难想到,所以这个地方我先给出结论,后面再证明 结论:一个指针从slow和fast的相遇点开始走,宁外一个指针从链表头开始走,他们会在环的入口点相遇(每个指针一次走一步),下面我们先来证明一下:

当我们写到这个地方就很明了了,我们有:L=(n-1)*C+C-X.这个地方的C-X就相当于我们从meetnode点开始走,然后(n-1)*C就相当于在环中走了几圈,这个地方相当于我们一个指针从head开始走(从链表的头),一个指针从meetnode开始走,它们最终会在入环点相遇(也就是从头开始走的指针走到距离L时在入环点,从meetnode开始走的指针也一定在入环点),期间从meetnode开始走的指针可能会在环内不止走一圈,但是不管它走几圈它们最终都会相遇. 我们有了思路后,代码写起来就很简单了.

---

---

3.2 代码实现

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode* slow=head;
    struct ListNode* fast=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)
        {
            struct ListNode* meet=fast;
            while(meet!=head)
            {
                meet=meet->next;
                head=head->next;
            }
            return head;
        }
    }
    return NULL;
}

---

---

3.3 方法二:相交链表法

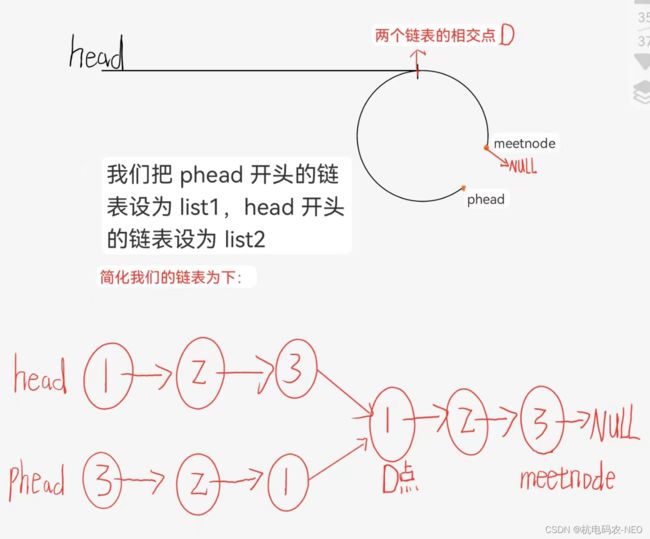
这个题还有第二种解法,我们之前做过一道相交链表的题,这个题可以沿用它的思路来解题,我们还是先找到slow和fast相遇的点记为meetnode,然后我们找到meetnode的下一个节点设为phead,将这两个节点断开,将pheaad设为新链表的新头,将meetnode置为空指针,我们来画图看看

这个题我们把一个链表拆成两个链表,就从一个环的问题转换为了两个链表相加的问题,即这个地方list1和list2的第一个相交点就是我们的第一个入环点.我们之前做过相交链表的思路,所以这个题也省去了一点功夫,但是值得注意的是,这个题的题目明确告诉了我们不允许改变链表,所以我们这个地方是不能把meetnode->next给置空的,虽然不能改变链表,但是这个题还是可以用这个方法来做. 这个地方想尝试一下这个方法的可以去看我的前一章链表题分享二,里面有详细的相交链表的解法.

---

---

---

4. 复制带随机指针的链表

4.1审题

先看题:

---

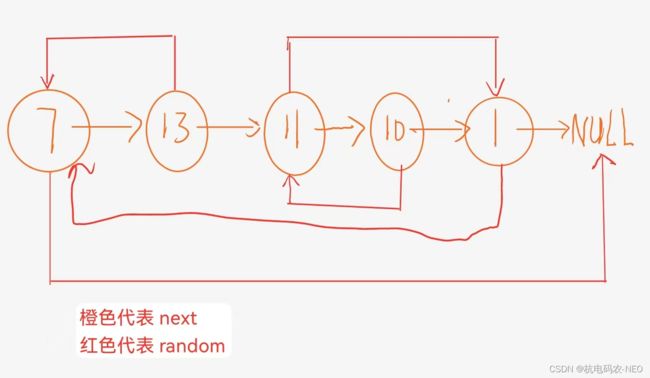
这个题让我们把它给的链表拷贝一份,然后再返回拷贝的链表,并且复制链表中的指针都不应指向原链表中的节点 ,假如这个地方没有随机指针random,我们就很好办,直接一个节点一个节点的复制最后再链接起来,这个题难就难在它里面有一个随机指针,你不知道原来的节点的随机指针指向的是哪一个位置,所以如果我们按照平常的思维解题,也就是暴力求解的话时间复杂度为O(N^2),实现起来也比较复杂,所以这个地方我们不要这种"笨办法".我们将拷贝的链表和原先的链表建立某种联系,这里我直接说结论:第一步:将要拷贝的链表一个一个拷贝后插入原先的链表当中,拷贝的链表的每一个节点在原先的链表对应的节点后面,使两个链表合并为一个如图:

---

当我们按照上面的方式将它们链接起来后,我们可以观察到原先的节点2的随机指针指向的是原先的节点1;那我们希望拷贝链表的节点2也指向拷贝链表的结点1,这个时候它们就有一个关系式, 我们拷贝链表节点X的随机指针等于原先链表的节点X指向的随机指针的next,放在这个题也就是拷贝链表的13的随机指针指向的位置是原先链表的13指向的随机指针的next;这里我们的第二步就出来了:在我们链接好的链表基础上,用我们刚刚发现的规律将拷贝链表所有的节点的随机指针的指向都给确定下来.

---

当我们解决了随机指针的问题后,这个题就很好办了,现在我们进行我们的最后一步,第三步:将我们的拷贝节点全部截取下来,并且重新链接组成一个链表(这里用尾插);注意这个地方我们还要还原原先的链表(不能说拷贝了一份链表就把原先的链表给破环了):

当我们推导到这个地方的时候就可以着手写代码了.

---

---

4.2 代码的分布实现

4.2.1 第一步:

struct Node* cur=head;
    while(cur)//第一步:拷贝节点插入原节点中
    {
        struct Node* copy=(struct Node*)malloc(sizeof(struct Node));
        copy->val=cur->val;//copy链表的值和原链表相同
        copy->next=cur->next;//此时cur的next还指向原先链表的cur的下一个节点
        cur->next=copy;//这个地方顺序不能换,要是先写这一句那我们就找不到原先链表的下一个节点了
        cur=copy->next;//最后再将cur移动到原先链表的下一个位置.
    }

我们不断开辟空间(也就是不断创建节点)和原先链表的结点相连接,并且保持val值相同.

---

4.2.2 第二步

    cur=head;//上一步的cur已经走到NULL了,这里重新把它置为head
    while(cur)//第二步:将拷贝的节点的random值确定了
    {
        struct Node* copy=cur->next;//上一个创建的变量copy已经在上一个while循环中销毁了(开辟的空间和指向没有销毁),这里重新定义一个copy变量
        if(cur->random==NULL)//当原先链表的随机指针指向空,我们就不用花里胡哨了直接将我们的拷贝节点置空
        {
            copy->random=NULL;
        }
        else
        {
             copy->random=cur->random->next;//这就是我们发现的规律
        }
        cur=copy->next;//cur还是不断的迭代往后走
    }

做完这最具技巧性的一步最后就剩把拷贝节点截取下来了.

---

4.2.3 第三步

struct Node* copyhead=NULL,*copyend=NULL;//先定义两个拷贝链表的变量,一个用来返回拷贝链表的头,一个用来迭代往后走
    cur=head;//重新将cur置空
    while(cur)//我们重新链接用的是尾插的方法
    {
        if(copyhead==NULL)//第一次进循环时先将copyhead和copyend赋值
        {
            copyend=copyhead=cur->next;
        }
        if(copyend->next==NULL)//这个地方是特殊情况,如若不讨论特殊情况会报错解引用空指针
        {
            cur=NULL; 
        }
        else
        {
           struct Node* next=copyend->next;//新定义的节点为原先链表的cur的下一个节点,定义这个变量的目的是当我们拆下一个
                                          //拷贝节点后,我们会找不到下一个原节点,cur就不能往后迭代着走
        copyend->next=next->next;
        cur->next=next;//回复原先链表
        cur=next;//cur往后迭代
        copyend=copyend->next;  //copyend也往后走,如果这个地方不定义copyend或者copyend不往后走的话,我们每次尾插都要重新找尾
        }
    }

---

当我们理解了这三个步骤后,我们将三个步骤合并一下组成我们最终的代码:

struct Node* copyRandomList(struct Node* head) 
{
	struct Node* cur=head;
    while(cur)//第一步:拷贝节点插入原节点中
    {
        struct Node* copy=(struct Node*)malloc(sizeof(struct Node));
        copy->val=cur->val;
        copy->next=cur->next;
        cur->next=copy;
        cur=copy->next;
    }
    cur=head;
    while(cur)//第二步:将拷贝的节点的random值确定了
    {
        struct Node* copy=cur->next;
        if(cur->random==NULL)
        {
            copy->random=NULL;
        }
        else
        {
             copy->random=cur->random->next;
        }
        cur=copy->next;
    }
    struct Node* copyhead=NULL,*copyend=NULL;
    cur=head;
    while(cur)//第三步,取下拷贝节点后尾插
    {
        if(copyhead==NULL)
        {
            copyend=copyhead=cur->next;
        }
        
        if(copyend->next==NULL)
        {
            cur=NULL; 
        }
        else{
           struct Node* next=copyend->next;
        copyend->next=next->next;
        cur->next=next;
        cur=next;
        copyend=copyend->next;  
        }
       
    }
     return copyhead;
}

---

---

---

5. 总结

虽然我们这一章只分享了三个题目,但是我们可以明显感受到这个地方的技巧性和思路都是很不好想的,是直接上难度了的.但是我们这个地方使用的快慢指针法和拷贝链表的思路是很经典的解题思路,第一次做的时候想不到是很正常的,小编第一次做这三道题的时候也是一个有技巧的方法也没有想到,硬着头皮去解,解到后面也是报错一场空.我也是后面去向前辈取经得到的思路和方法,所以说我们是站在巨人的肩膀上学习编程,自己想不出技巧没有关系,消化吸收前辈的经验和技巧也是我们提升自己的方法.我们不断的做题不断的总结,下次遇见相似的思路或相似的题我们也就不愁了.这个地方的三个题目需要我们自己画动态图去分析,每一个结论或是每一个方法想要熟悉它.掌握它都需要我们慢慢画图去理解.最后想说,我们到这里才开始真正的去"玩"这个链表,我们的链表到这里才刚刚开始,各位加油!