信号完整性基础02：从电感、电容到理想传输线（2）

说在开头：关于元素周期表

让我们将时间回拨到1857年，出生在穷乡僻壤——西伯利亚的寒门学子门捷列夫（俄国最伟大的化学家）被破格录用为圣彼得堡大学的化学讲师，此时的他工资微薄，不得不到处家教补贴家用。这并不是个别现象，连他的老师齐宁初入职场时也要兼职家教，那时有个从瑞典来的工程师拖家带口的来到俄国，帮助沙皇研制水雷，齐宁就是那个工程师儿子的家教老师，这个十来岁的小p孩聪明绝顶，对化学非常在行，他的名字是：阿尔弗雷德.诺贝尔。没错，就是那个日后大名鼎鼎的炸药大王，诺贝尔奖设立者；所以从理论上来说，诺贝尔和门捷列夫是师兄弟的关系。

1863年，化学家们已经发现了63种元素，那几年平均每年都能发现一种新元素。而在此之前化学家们已经发现了元素的化学性质似乎表现出了周期性的规律：德国化学家德贝莱纳提出了“三元素组”观点，法国人德尚寇特斯提出元素性质的“螺旋图”，德国人迈尔发表了“六元素表”，英国人纽兰兹又提出“八音律”。门捷列夫也在研究元素之间的联系和规律，但是周围的人以及他老师齐宁都不支持他，在他们看来元素相互之间并没有什么联系。

门捷列夫从小喜欢打牌（兴趣的重要性体现出来啦~），他做了很多卡片，每一张都写了元素的名称、原子量、化合物的化学式和主要性质。之后他把卡片加以系统排列：

1. 他先把卡片分成三组，按元素的原子量大小排列，但毫无规律可循；

2. 把它们排列成几行，再把各行中性质相似的元素排成列。

门捷列夫突然激动起来：这样排列后，每一行元素的性质都是随着原子量的增大自上而下逐渐变化，元素的排列是有规律的！但是锌和砷之间还留有两个空位，这又是为什么呢？门捷列夫思考良久，又激动了起来：这两个空位就是尚未被发现的元素啊，而且它们的性质应该与铝和硅相近。

门捷列夫在化学元素符号的简单排列中发现了规律，但是他发现列表中的排列还不完善，于是找到各种与之有关的学术杂志，反复研究，发现杂志上某些化合物的性质和组成的材料常常相互矛盾，于是他认为：这是因为原子量测定不准确而造成的，才使得他的元素表中有些元素没能排在与其性质相符的位置上。于是他决定亲自进行实验，重测了一些元素的原子量，经过半年的努力，他发现有些的确与别人的结论不符；于是按照自己测定的原子量把它们排列在性质相近的元素行列中。1869年3月，门捷列夫发表了一篇题为《元素性质与原子量的关系》论文，首次提出了元素周期律，世界上第一章元素周期表诞生了。他预言并描述了当时科学界还不知晓的三种元素：“类硼”，“类铝”和“类硅”的性质。

但是门捷列夫的论文并没有引起多大的关注，还需要新元素来证实他的预言，6年后的一天，他在翻阅法国科学院报时，看到一篇有关勒科克.德布瓦博德兰发现的一种叫作“镓”的新元素，发现这个元素的性质与他预言的“类铝”性质很相似，但法国科学家测定镓的比重为4.7，而门捷列夫根据元素周期表推算却是5.9，于是门捷列夫写信给勒科克，告诉他所测定的镓的比重不对。勒科克看到门捷列夫的来信后一脸懵逼：门捷列夫手头又没这个元素，怎么能断定自己所测定的比重不对？不过测比重是很容易的事情，为慎重起见就再测量一次吧。结果勒科克信服了。

门捷列夫是对的，镓的发现在科学界引起了强烈地反响，门捷列夫和勒科克立即闻名全世界。此后，瑞典科学家尼尔森又发现了一个新元素，与门极列夫所描述的“类硼”符合，尼尔森将它取名做“钪”；德国化学家文克勒发现了新元素“锗”，又验证了“类硅”元素的预言。元素周期表获得公认后，各种荣誉潮水般的涌向门捷列夫，他被多个国家的科学院聘为外籍院士。1905年门捷列夫被提名诺贝尔化学奖，但他最终没得到诺贝尔奖，因为评审委员中有个科学家跟他有私人恩怨，这一年的诺贝尔奖颁发给了莫瓦桑，到了来年，大家觉得这一回总该轮到门捷列夫了吧，哪知道门捷列夫突然去世了。

门捷列夫说过：天才就是这样，终身劳动便成天才。他真的工作到最后一刻，由于突发心梗，于1907年2月2日与世长辞。在他的葬礼上学生们举着的大横幅上写着一系列的符号，上面写着H、Fe、Zn……等。

门捷列夫虽然发现了元素的周期律，随着原子量的增加，每隔一段就会出现元素性质近似的情况。但元素周期律背后还蕴含了怎样的规律呢？门捷列夫也不知道：各位，“坑”我就挖在这儿，你们谁有本事谁就去填，反正我先走一步了。这个秘密要到几十年后的“上帝之鞭”泡利来解答，而此时泡利还刚上小学哪。（参考自:吴京平-无中生有的世界）

三，集总和分布模型

对于信号传输来说，我们之前已经讨论过了，其实就是电磁波的传播。所以对于电路长度来说：重要的不是走线电路本身的尺寸（长度），而是电尺寸（电路尺寸/波长）。那波长又表示啥意思呢？

如下所示，波长代表了电磁波相位改变360°时传播的距离。好，大宗师麦克斯韦的方程组当然可以解释所有的电现象，但这东西太复杂了，也不便于应用啊。那是否有方法能够简化的呢？

有一种近似的方法：采用集总模型和基尔霍夫（大宗师）定律来分析。那什么时候才能用集总模型和基尔霍夫（大宗师）定律来简化大宗师的方程组呢？

答案是：当电路最大尺寸为电小尺寸时。那又如何定义电小尺寸呢？

举个栗子，只要电路尺寸（PCB走线长度）远小于信号波长就行了；一般来说当电路的最大尺寸（走线长度）小于信号最高频率波长的1/10时，就认为是电小尺寸。好，那我们来总结一下：当PCB走线（线缆）长度小于信号最高频率对应的波长1/10时，就认为是集总模型，可以用基老师的定律来整，那就很简单了。

如下图所示，作为时间t的函数正弦波电流，从左侧输入右侧输出，该电流是以速度v（如果在真空中为光速：30万公里/秒）传播，那么穿越元件和连接线的电流所需的时间延时Td = L/v。举个栗子，3GHz信号的边沿时间大概在100ps~300ps左右；在PCB带状线上的信号传播速度比空气中要慢（介电常数更高），大约是1.8*10⁸ m/s（v0 = 1/[√(ε0*μ0)* √(εr*μr)] = 3*10⁸/√εr m/s ），因此6in长的带状线延时大概为850ps；以当前的这种信号边沿与传播延时之比，会造成数字逻辑电路中的问题。

当连接线长度等于一个波长的距离，即L = λ时，信号从a点到b点经历的相移为360°，即a点输入与b点输出的电流是同向的；同理，如果L = λ/2时，相移为180°，即a点输入与b点输出的电流是反向的；那么如果L = λ/10时，那么电流相移为36°；L = λ/100时，那么电流相移为3.6°。如果像集总参数电路模型假设的那样，连接线的影响不重要，那么连接线的长度导致的相移是可以忽略不计的（可以看成通过纯粹阻、容、感连接的电路）。对此，其实并不存在固定的准则，要求电尺寸的大小；但是一般情况下，如果连接线长度小于信号激励源频率对应波长的1/10，那么我们就假定相移可以忽略不计。在一些特殊情况下，可能要求更高。

——对电路设计来说，电尺寸比PCB走线长度（电路尺寸）更重要，因为当走线长度小于波长的1/10时，信号经过该距离的传播后的相移可忽略不计，所以此时连接线可认为是电小尺寸。

所以我们需要能够根据某特定频率计算出电尺寸，举个栗子：在空气中1m长的线缆正好是300MHz频率对应的一个波长；因此在根据尺寸的近似比例，可以很容易计算出在空气中的另一个频率的波长；例如，50MHz的波长是：1m*300MHz/50MHz = 6m；而2GHz的波长是：1m*300MHz/2GHz = 0.15m。

那么我们计算电尺寸来判断一个电路是否为电小尺寸（L < λ/10），如果是电小尺寸，就可以运用比电大尺寸（L > λ/10）更简单的集总参数电路模型，采用基尔霍夫电压和电流定律；如果是电大尺寸（分布参数电路模型），那么只能运用麦克斯韦方程组或则用一系列集总参数电路串行来近似。对于分布参数电路模型来说，电磁波的滞后效应不可忽略，沿线传播的电磁波不仅是时间的函数，而且是空间坐标的函数。

四，什么是传输线

1，传输线的定义

讲完了电感和电容终于开始本章的正题：传输线。那传输线到底是个什么鬼，什么样的导线能称之为传输线？我们必须要先从传输线定义出发（苏格拉底说，我们对任何一个事物进行讨论，首先要明确其定义。ps：这句话是我编的。），传输线就是：由两条有一定长度的导线组成，把电磁能从电路的一端送到电路另一端的装置。为了更加清晰的理解这个概念，我们接下来用两个方面来阐述：

1. 从传输线的物理结构描述：是由两条有一定长度的导线组成；接下来咱们逐字分析：

1, 两条：从某种意义上来说是对的，因为信号的传输就是通过：信号路径和回流路径，这两条“导线”来实现的；但实际信号传输过程中，特别是回流路径往往并不是简单的一条路径，而是根据其固有物理规律（回路阻抗最小）自行选择的n条回流路径；从另外一层意义上来说：传输线说的就是信号路径与回流路径之间的关系，与其它（电源、地）无关；

——之所以是n条，因为信号路径上的信号频率一般不是单一频率（有很多频率分量等等），所以不同频率分量就对应了不同的回流路径，很难确定具体的回流路径（后续在《电磁兼容性基础》中具体分析）。

2, 一定长度：固定长度的导线对于信号A是传输线，可能对信号B来说就只是导线；对于传输线来说，导线长度与信号的边沿时间强相关，它要满足分布系统模式（导线长度大于或等于波长），在短线模式或集总系统中的导线不再是传输线（不适用传输线模型的相关理论），而只是导线（运用基老师的定律就能搞定了）；

3, 导线：佛陀在金刚经中说：“如来说世界，即非世界，是名世界”，佛说这个真实的世界，并不是我们用“眼耳舌鼻身意”所观察到的世界，只是用“世界”这个名字来称呼它罢了；我借用这段话：定义所说导线，即非导线，是名导线。这个真实的线段并不是我们脑中的一根具体导线，它只是一个名称；导线可以由非常多的形态呈现出来。

2. 从传输线的功能描述：把电磁能从电路的一端送到电路另一端的装置；

1, 电磁能：传输线传输的是电磁波；那么什么是电磁波呢？

(1) 固定的3.3V电平或0V电平是电磁波么？很明显，固定电平并不会产生电磁波，电磁波的传播只发生在信号发生跳变的一瞬间；

——固定电平只有固定的电场和磁场，而非交替出现的电磁场（电磁波）。

(2) 传输线只传输由3.3V变成0V或则0V变成3.3V的这些信号边沿，固定的电平不是传输线所传播的（非常重要！）；所以高速还是低速信号的判断不在于信号本身频率的高低，而在于传输信号边沿的快慢（最高频率分量）。

——但是信号本身频率更高，往往意味着边沿跳变更快，它们是有关联的。

2, 从电路的一端送给电路另一端：电磁能的传输需要从发送端传到接收端，需要保证的是接收端信号能够被正确的接收，而不是要求发出端的信号完整，这是传输线的意义所在。

——举个栗子，我们测试信号质量的时候是选择发送端还是接收端呢？明显是接收端，但一不小心测了发送端，发现发送端的信号质量很差，会不会有问题呢？发送端信号质量差是正常的，后续章节详细解释。

2，传输线如何工作

我们在传输线的定义中说了，传输线就是信号路径与回流路径这两条“导线”之间的“暧昧故事”（你是谁，我是谁，哦，谁也离不开谁~），只是在实际设计中，回流路径往往是回流地或电源，但我们需要明确地将：回流路径的概念与回流地/电源区分开，避免导致概念的混淆。

1. 如下图所示，只有当信号路径相对回流路径有电压跳变时（信号前沿），信号路径上的电流通过互感和电容（信号路径相对于回流路径）流向回流路径（位移电流）；

——需再次强调：传输线模型只使用于跳变信号（信号前沿），对于固定电平，传输线模型的电感和电容不起作用（电感短路，电容开路），此时起作用的只是导线的串联电阻。

2. 那么又有一个问题了：假设有一个导线从地球延伸到月球，此时传输线延时约为1.2s（约38万公里）：信号电流从地球向月球传输，返回电流从月球向地球传输形成一个电流环路，那么返回电流是信号电流到达月球后，再从月球发送回来的么（总共经过2.4s）？

1, 从上图可以看到，当信号电流从地球（源端）发出的瞬间，就开始对传输线电容进行充电：电流从芯片电源->芯片驱动管脚->信号路径->电容->回流路径->芯片电源，形成一个完整的回路，即返回电流是跟随信号电流即时产生的；

2, 信号还未传到远处时，它还不知道后面的传输线结构如何，电流已经过返回路径回到源端，仅仅与信号前沿的环境（介电常数和磁导率等）和信号前沿所在的那一小段传输线有关；

3, 所以，一旦信号路径中信号发出，回流一直存在，直到在接收端的回流返回到源端，总共花费时间是：2倍的走线延时（举个栗子：地球与月球之间延时的两倍：2.4s）。

那我们现在可以更简单来表述传输线的工作：

一， 只有在信号前沿（跳变）处的导线才工作在传输线模式，且信号状态只与信号前沿所处位置有关；

——只有信号边沿（特定时间）所占据的那段导线（特定位置）才是传输线；并非导线的任何时刻、任何位置都是传输线。

二， 信号一旦从源端发出，信号回流即时返回到源端。

3，传输线如何回流

我们上一节说传输线的回流路径并非一定要是GND平面，那么对于回流平面不是GND平面的情况下是怎样的呢？或则说就算回流是GND平面，回流是怎么走的呢？

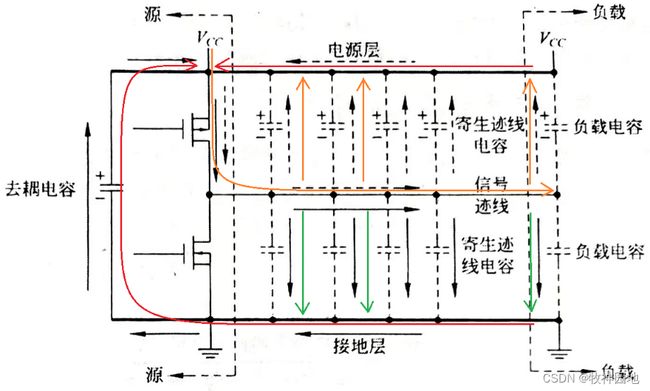
举个典型的栗子，如下图所示，一条带状线（什么是带状线？置于2个平行的地平面（或电源平面）之间的电介质之间的一根传输导线）上层是电源平面，下层是GND平面，那么信号线中传输信号时，它会智能地选择GND平面来作为回流么？

1. 当信号线上的电平由低（0）到高（1）跳变时，其电流通路如下图所示；

1, 首先，我们必须要清楚电流从哪里流出来，必然要流回到哪里去；所以当信号线从0—>1跳变时，这些电流是从哪里来的呢？对于CMOS电平驱动来说，其必然来自于器件的电源管脚VCC；

2, 电流从VCC通过MOS管流向信号线，信号线上的电流不断通过信号路径与回流路径之间的电容，要返回到VCC去；

3, 但是对于信号来说，它并不清楚上面那层是VCC平面，下面那层是GND平面，所以信号边沿只会根据所处的电路结构来决定回流到VCC平面和GND平面的电流大小；

——所谓的电路结构，是指信号线与VCC之间的距离（寄生电容）和信号线与GND之间的距离（寄生电容）大小。

4, 两组信号回流路径如下：

(1) VCC平面作为回流路径（黄色箭头）：VCC平面à输出器件VCC电源管脚，阻抗非常小；

(2) GND平面作为回流路径（绿色箭头）： GND平面à输出信号器件附近的GND平面à去耦电容返à输出器件VCC电源管脚。

——相对回流到VCC平面来说，回流到GND平面的回流反而具有更大的阻抗：去耦电容容抗；当然去耦电容容抗对于高速信号来说也是非常小的，举个栗子：10uF陶瓷电容器，理想情况下（不考虑寄生电感）在10MHz的容抗是：|Zc| = |1/jωC | = 1/2πfC = 1.6mΩ；那如果10nF陶瓷电容器（不考虑寄生电感）在100MHz下，容抗也只有160mΩ。所以基本可以忽略不计。

2. 当信号线上的电平由低（1）到高（0）跳变时，其电流通路如下图所示；

1, 当信号线从1—>0跳变时，信号线通过下管MOS管驱动到GND，所以信号线上的电流流回到输出器件内再到器件GND管脚；

2, 那么从信号线上的电流是从哪里来的呢？由上图可以看出，这些电流是从VCC平面和GND平面（回流路径）中来的；电流通过VCC平面和GND平面上寄生电容流向了信号线；

——为什么GND平面也会有电流流向信号线？因为信号线与GND平面间电容起始状态是充满电（有电压差）的，当信号线瞬间降低到0电平，电容两端必须有电流释放出来（GNDà信号线方向）；同理信号线与VCC平面之间寄生电容时没有电压差的，当信号线瞬间降低到0电平时，必须进行充电（VCCà信号线方向）；所以VCC平面和GND平面都有电流流向信号线。

3, 我们知道：电流从哪里来，那它必将回到哪里去；所以它们从VCC和GND平面（回流路径）中出来的电流，必将会从输出器件的GND管脚出发，返回到VCC和GND平面（回流路径）中去；

——电流必将回到信号路径对应的回流路径位置的VCC和GND平面上，我们可以将它看成一个实体的电容器来理解：举个栗子，从电容器的+端输出电流，必将回到它的-端去。

4, 两组信号回流路径如下：

(1) VCC平面作为返回路径（黄色箭头）：从输出器件的GND管脚à去耦电容à输出器件附近VCC平面àVCC电源平面；

(2) GND平面作为返回路径（绿色箭头）：从输出器件的GND管脚àGND平面。

所以我们可以得出一个结论，从原理上来说：信号的回流路径是GND平面还是VCC平面，是完全等价的。但为什么我们一般都要选择用GND作为回流平面呢？我认为主要原因在于：

1. 在单板上，不同的器件之间的GND一般是同一个，而且会铺有完整的GND平面；

2. 单板上的电源种类有很多，一般不同电源会对电源层进行分割，所以如果以电源平面作为参考，一般情况下会出现回流不连续的情况；

3. 并不是所有的VCC平面都可以作为回流路径的，最好是器件的I/O电源，起码是输出器件的电源（例如Core电源）；但如果不是输出器件的电源，那么回流路径会出现不连续，导致传输线阻抗不连续。

——如果是输出器件的Core电源，那么回流到输出器件后，那么回流路径时：core电源à去耦电容àGND平面à去耦电容àI/O电源平面；如果回流平面是其它器件的电源，那么回流路径就是从电源平面à去耦电容àGND平面àI/O电源平面；这两种情况的差别在于同I/O电源平面之间的距离，如果是同一个器件，那么距离相对较近，构成的回流环路比较小（阻抗变化小），但如果是其它器件，那么构成的回流环路将会比较大（阻抗变化大）。

4，传输线的阻抗与时延

传输线最重要的两个特征是：1，特征阻抗；2，时延（信号传播速率）。

我们知道信号在传输线上传播的过程中，其电压/电流（阻抗）的特性类似电阻，无损传输线可以很好的近似传输线的特征阻抗和时延特性，计算也相对方便，所以先用该模型进行分析。

4.1 传输线阻抗

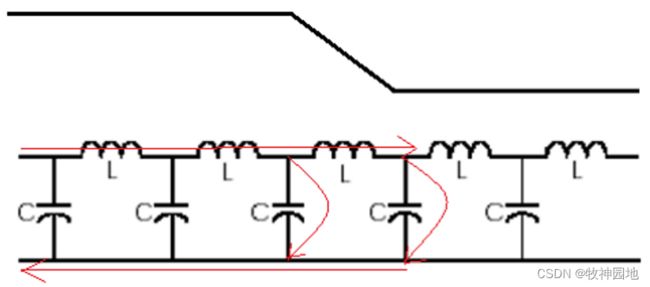
如下图是无损传输线模型，以及在信号传输过程中的电流完整的流动过程，我们用电感L和电容C来描述传输线的回路电感和电容；

1. L在如下拓扑中，指的是回路电感，这是一个等效电感：不是信号路径的局部电感，而是信号路径与回流路径构成的回路电感；所以该电感跟回流路径强相关。举个栗子：当传输线信号路径不变，而回流路径不连续时（例如：信号线的参考GND层被分割，回流路径就要绕远路），传输线的电感会增大；

——如之前所述传输线电感展开如下图：Lloop = L1+L2-2*L12；

2. C在如下拓扑中，指的是信号路径相对于回流路径之间的电容。

——举个栗子：信号线与回流地之间的板间电容，其间距是PCB层间距，介电常数是FR-4材料的参数。

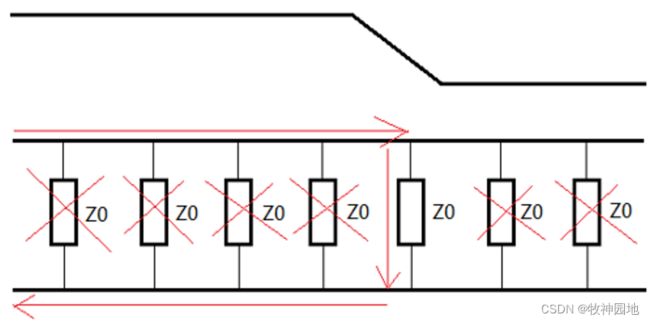
我们知道无损传输线的阻抗模型等效为：很多组串联在信号路径上的L和并联在信号路径与回流路径之间的C组成；而且电流是从信号路径到回流路径的方向，由此得出传输线的阻抗可以等效为搭接在信号路径与回流路径的一个电阻（并联电阻），如下图所示。搞错没得？这跟之前看到过的传输线等效模型完全不一样啊，隐约记得之前看到的特征阻抗似乎是串在线路上的诶。

的确这个并联的模型好像有致命问题：如上图所示，如果传输线的阻抗是搭在信号路径与回流路径之间的电阻，那么这么多电阻并联后应该是Z0/n而不是Z0，假如有一根无线长的导线（我是村长儿子，可以随意假设），那么特征阻抗就几乎为0了么？这违反了常识和电路的基本原理啊。

挠了半天的头，还是先回到传输线的定义来看看：信号在传播过程中只有信号前沿的那部分导线才能看成是传输线。原来如此，如下右图所示，在信号跳变的左侧是高电平（例如3.3V），右侧是低电平（0V），信号路径与回流路径上的电压差保持不变，没有发生充放电的动作，所以这些地方阻抗是无穷大（导线上的信号是固定电平，则信号路径和回流路径之间电压不会变化，此时电容不会进行充放电，所以电流I = 0；而Z =U/I = ∞，相当于断开）；只有处于信号前沿的信号路径与返回路径之间进行着充放电的动作，电容和电感才有了用武之地，成为特征阻抗：Z0。如下图所示。

那结论就出来了：传输线的阻抗是信号前沿（跳变）处所受到的阻抗，它是一个瞬时的阻抗。所以传输线阻抗也可以看成串接在信号路径上的一个电阻。

好，我们现在来总结传输线阻抗的描述：传输线阻抗是信号在传输过程中，信号前沿所受到的信号路径与回流路径之间瞬时阻抗。

如果传输线的瞬时阻抗在整条导线上都保持恒定（传输线瞬时阻抗保持一致），那么我们称之为：传输线的特征阻抗。传输线特征阻抗的特点是：它只与介质材料、传输线结构相关，与传输线长度无关。

这章我们思考了太多的问题，也不差下面两个问题：

1. 信号边沿的快慢会导致边沿所占传输线长度不同，阻抗会不同么？信号的频率与传输线特征阻抗有关么？（不考虑信号频率导致的FR-4材料介电常数的变化）

2. 我们怎么去理解阻抗不连续导致的反射和传输呢？（根据传输线模型分析）。

——自己思考哈，我就不替大家费脑子了。

4.2传输线时延

传输线时延指的是：信号在传输线上传播过程中，电场与磁场建立的快慢。需要明确的是，如我们之前章节所分析，它区别与导线中电子移动的速度（1cm/s左右）：金属导线中电子移动的快慢决定导线电流的大小（Q= I *t）。

信号传输本质上是电磁波的传播，受到介电常数和磁导率的影响，铜线和板材介质相对磁导率是1，不影响信号传播速率，所以信号传播速度主要受到介质介电常数的影响。

1. 通过麦克斯韦大宗师的方程组得到，电磁波传播速度：V = 1/√(ε0*εr*μ0*μr)= 11.8/√εr in/ns；介电常数越大，信号传播速度越低，传输线延时越大。

2. 通过传输线电感和电容来表示传播速度：V = 1/√(LC)（L：单位长度回路电感；C：单位长度电容）。

从直观的逻辑分析两个信号传播速度公式：V1 = 11.8/√εr 和V2 = 1/√(LC)，是否等价来加深理解（当然通过数学模型可推理计算得到它们之间是等价的，ε和μ其实分别表征了传输线电容和电感的大小）；假设某一条传输线的初始V1 = V2：

1. 当εr增加，V1=11.8/√εr 平方根成反比减小；对V2来说，εr增加对电感L没有影响，C=εr*A/d 与εr成正比，导致V2= 1/√(LC)与εr平方根成反比减小；所以减小比例相同，所以V1 = V2；

2. 同理εr减小，还是能得出V1 = V2；

3. 当传输线走在内层（带状线），中间有一段回流路径不连续，此时不连续段传输线的介电常数没有发生变化，从V1的计算公式可得传输线传播速度不变；但此时由于信号路径与回流路径距离变远，导致此段传输线回路电感L增加（与距离/成正比，L = μ0*μr*N²*Ae/L = μ0*1*1*l*h/1 = μ0*l*h，其中Ae：回流面积；l：导线长度，h：信号路径与回流路径的距离），而传输线电容C减小（与距离成反比）；

4. 更复杂条件的改变需要仿真软件支持计算。

那么我们可以得到一个结论：在同一介质材料（相同介电常数εr）中信号传输速度V = 1/√(LC)是保持不变的，不会因为导线结构的改变而改变，由于各种情况导致的L或C的改变，可以很好的定性分析对应C和L的变化。

那么如果有一条传输线长100mm，我们在传输线每隔1mm的地方接1nF电容，那么传输线的信号传播速度（传输延时）是否会变化？为什么？

5，有损传输线

实际传输线总是存在损耗的，有损传输线的模型如下图所示，除了串联回路电感和并联电容之外，还有串联电阻和并联电导；传输线的损耗主要就来自于这两部分电阻。

——咱们是学过阻容感专题的，都知道电感和电容只能存储能量，而不会消耗能量。

1. 串联电阻是指：金属导线本身的电阻，在直流条件下导线本身电阻是非常小（mΩ级别）；

——随着信号频率的增加，由于趋肤效应导致导线电阻增加，造成导线对信号的损耗。

2. 并联电导是指：导线（信号路径）与回流路径之间的漏电流，由于介质材料是绝缘材料，介质本身电阻非常大，所以在直流条件下电阻非常大（漏电流为nA级别），可以忽略不计；

——随着频率的增加，随着电场变化介质中偶极子运动产生了更大的损耗（介质损耗）。

3. 对于传输信号来说，不管是串联电阻还是并联电导都会造成信号高频分量更大的损耗，高频信号分量损耗的大小决定了传输线的传输带宽；

4. 假定εr在频率中保持不变（实际应用中εr会随频率升高而减小），如下图中α为传输线衰减常数，β为相移常数：

1, 在高频时电阻分量远小于感抗，所以传播速度接近无损传输线；

2, 在低频时电阻分量不可忽略，其传播速度小于无损传输线；

3, 所以信号的高频分量的传播速度要大于低频分量的传播速度，会导致信号上升沿先快后慢。

当然对于高速信号，我们可以有几个方法来降低传输线损耗的问题：

1. 选用低损耗介质（不是低介电常数）；

2. 尽量减小导线长度；

3. 增加导线宽度，但这会影响差分阻抗，影响差分线之间耦合度。

写在最后

本章是信号完整性的基础（重中之重，如果有任何的疑问，需彻底想清楚），后面所有的理论需要基于对传输线的正确理解之上。我也是捋了好长时间才捋了这么一点出来（后续《电磁兼容设计基础》专题会再更深一层）。当然我们在后续的章节中，还会不断用到传输线这个基本概念，用那些个理论：反射、串扰、差分线及EMI辐射等等来验证并加深理解。

本章部分相关内容和图片参考自：Eric Bogatin-《信号完整性分析》；克莱顿.R.保罗-《电磁兼容导论》。下一章《反射与阻抗匹配》。