优先级队列--priority_queue
priority_queue
- 适配器
- priority_queue
-
- 与队列的不同点
- priority_queue实现的功能
- 复习一下堆
-
- 图解堆删除元素的过程
- 堆的向下调整,对应pop
- 堆的向上调整,对应push
- 优先级队列的实现
-
- 先列一个大的框架
- 关于队首元素大小的问题
适配器
适配器简单的来说就是一种设计模式,C++的STL中的大部分模板都有着相似的功能,与相同的接口函数名,类似于这样的:
- push_back(); pop_back(); push_front(); pop_front();
- size(); empty();
所以说对于这种类型的容器,就可以对他们进行封装,从而实现一些列的功能,就比如说:
- stack,queue
- deque,priority_queue
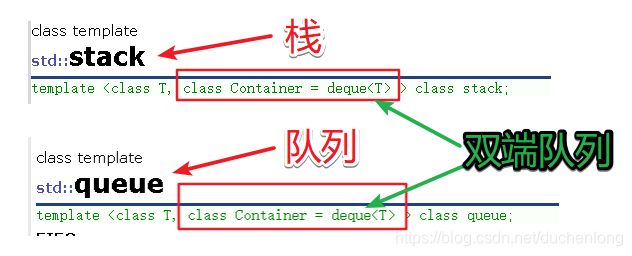
虽然对于队列和栈,我们也可以用一些数据结构来实现,但是他们的功能STL中的其他容器都具备,所以STL中并没有将stack和queue划分在容器这一类,而是用了一个容器适配器。
有了容器适配器,我们就可以根据不同的使用场景来确定使用不同的容器
- 经常要头插元素的话,我们就可以使用
list当做适配器的类型,因为他的底层是一个带头结点的双向循环链表,头插时间复杂度是O(1) - 如果要经常访问元素的话,我们就可以使用
vector作为适配器的类型,他的底层是一个数组,数组对于访问的时间复杂度是O(1) - 在STL中他是用一个
双端队列deque来实现的,他结合了list插入效率高,以及vector访问效率高的特点。但是他却不适合遍历,他的内部是一段一段的有长度的地址区间,每一次访问都需要检测是否越界,所以遍历有些困难。
priority_queue
priority_queue,翻译过来就是优先队列的意思。
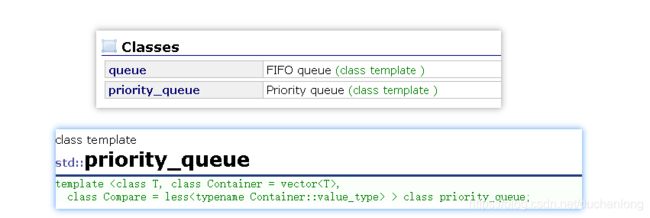
他是一个封装在queue中的一个容器适配器,底层默认是用vector来实现,并且默认是降序,也就是默认是一个大堆。
与队列的不同点
队列作为一个先进先出的标准数据模型,它内部的数据不能保证有序。
STL基于这一特点,对queue做了改进,让他每一次出队的数据保证是当前队列的最值(最大值,最小值),但是却不满足了先进先出的特点。
因为优先队列需要满足每次front()都是队列的最值,还有不停的插入元素,那么单纯的用sort()函数进行排序是不行的,因为他每一次的时间复杂度都是O(n * log(n))。
这个时候就可以使用堆,建一个大根堆或者小根堆,每一次获取队头元素都是堆顶的元素,都是可以保证是最值,而且插入删除再次建堆的时间复杂度也只是O(log(n))。
priority_queue实现的功能
- pushk();,尾插一个数据 ,内部进行向上建堆
- pop();,删除队头数据,也就是队列中的一个最值,然后内部进行向下建堆
- top();,返回队列中头部元素,也就是队列中的最值
- size();,返回队列中元素的数量
- empty();,判断队列是否为空
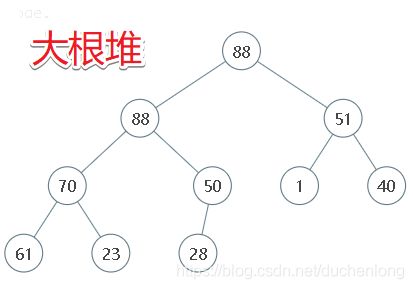
复习一下堆
堆是一种特殊的二叉树结构,他的每一个根节点都是这棵子树的一个最值(最大值或者最小值)
- 根节点是最大值,这是一个
大根堆 - 根节点是最小值,这是一个
小根堆
他的存储可以用一个数组来实现,不必建一个二叉树。这里有一个注意的点就是:(假设父亲节点为parent)
- 当你选择的第一个元素的下标为0,那么他的左孩子节点就是
parent * 2 + 1 - 如果选择第一个元素下标为1,那么他的左孩子节点就是
parent * 2
说到这个不禁想起上学期期末的数据结构考试,考试之前自己实现了一下堆,当时用的是数组嘛,下标都是从0开始的,这样求左孩子节点是
parent * 2 + 1考试的时候问了二叉树的左孩子节点,想都没想,直接
parent * 2 + 1,事后才发现,二叉树根节点是按照1算的,也就是parent * 2
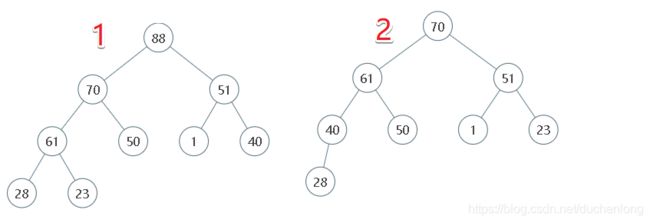
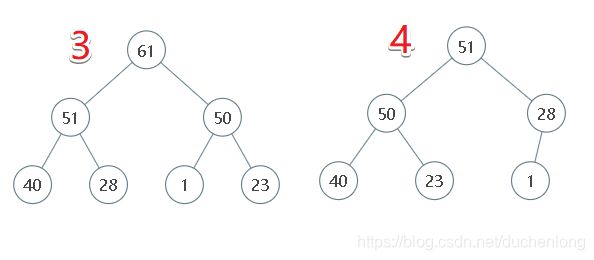
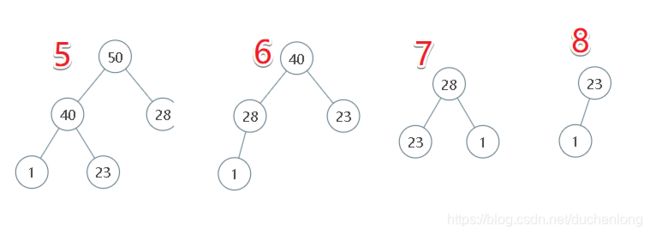
图解堆删除元素的过程
堆的向下调整,对应pop
- 向下调整一般是建立在删除或者排序的时候,这里因为vector数组的原因,删除的时候选择先交换,再删除末尾元素。因为删除开始位置的元素开销太大
- 向下调整的开始点一般在根节点的位置
//向下调整,数组默认以0开始
void AdjestDown(vector<int> arr,int parent)
{
size_t child = parent * 2 + 1;
size_t len = arr.size();
while (child < len)
{
//找左右孩子中最大的
if (child + 1 < len && arr[child]< arr[child + 1])
child++;
//判断孩子和父亲
if (arr[parent] < arr[child])
{
std::swap(arr[child], arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
堆的向上调整,对应push
- 向上调整有一个前提,那就是调整之前的堆必须是一个合格的大根堆或者小根堆
- 向上调整一般是建立在插入一个元素的前提下,所以出发点在新插入的位置,也就是数组的末尾
//向上调整,在原有堆的基础上调整
void AdjestUp(vector<int> arr,size_t child)
{
size_t parent = (child - 1) / 2;
while (child > 0)
{
//如果父亲节点的值比孩子节点的值小,就交换,然后继续下一次比较
if (arr[parent] < arr[child])
{
std::swap(arr[child], arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else//此时父亲节点比孩子节点的值大,说明已经是一个合适的大根堆了
break;
}
}
优先级队列的实现
先列一个大的框架
//优先级队列中默认是建立大堆,小于号的重载
template<class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue
{
public:
//构造函数调用适配器的构造
priority_queue()
:arr()
{}
//入队
void push(T x);
//出队,删除队头元素
void pop();
//返回优先级队列中元素的大小
size_t size() const;
//判断优先级队列是否为空
bool empty() const;
//堆顶元素不允许修改,可能会破坏堆的结构
const T& top()const;
private:
//向上调整,在原有堆的基础上调整
void AdjestUp(size_t child);
//向下调整
void AdjestDown(size_t parent);
private:
Container arr; //存储模式
Compare com; //比较的访函数
};
关于队首元素大小的问题
我们之前看到,优先级队列的模板有三个:
- 队列中元素的类型
- 队列所使用的适配器,默认是
vector - 队列的比较访函数,默认的
<比较,建大堆
如果比较的访函数是
<,那么就是建立大堆
如果仿函数是>,那么就是建一个小堆
//建大堆
template<class T>
struct less
{
bool operator()(const T& left, const T& right)
{
return left < right;
}
};
//建小堆
template<class T>
struct greater
{
bool operator()(const T& left, const T& right)
{
return left > right;
}
};
- push,插入元素 + 向上调整
//入队
void push(T x)
{
arr.push_back(x);
//向上调整,选择传一个有效的位置
AdjestUp(arr.size()-1);
}
//向上调整,在原有堆的基础上调整
void AdjestUp(size_t child)
{
size_t parent = (child - 1) / 2;
while (child > 0)
{
if (com(arr[parent], arr[child]))
{
std::swap(arr[child], arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
- pop,出队 + 向下调整
//出队,删除队头元素
void pop()
{
//队列中要有元素
if (empty())
return;
std::swap(arr.front(), arr.back());
arr.pop_back();
//向下调整
AdjestDown(0);
}
//向下调整
void AdjestDown(size_t parent)
{
size_t child = parent * 2 + 1;
size_t len = arr.size();
while (child < len)
{
//找左右孩子中最大的
if (child + 1 < len && com(arr[child] , arr[child + 1]))
child++;
//判断孩子和父亲
if (com(arr[parent], arr[child]))
{
std::swap(arr[child], arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
- size(),返回队列元素个数
//返回优先级队列中元素的大小
size_t size() const
{
return arr.size();
}
- empty(),判空
//判断优先级队列是否为空
bool empty() const
{
return arr.empty();
}
- top(),返回队头元素
这里需要注意,因为队头元素不能进行修改,一旦修改可能就会改变堆原本的结构。所有返回值需要加const修饰
//堆顶元素不允许修改,可能会破坏堆的结构
const T& top()const
{
return arr.front();
}