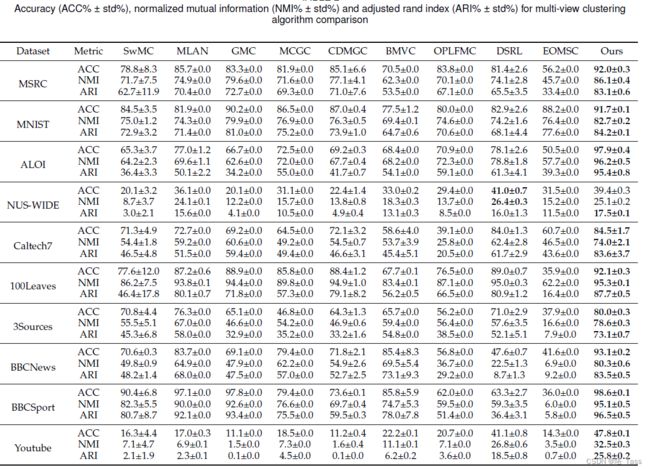
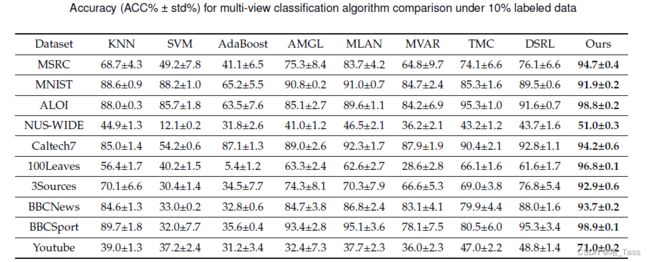
【论文阅读】Differentiable Perspective for Multi-View Spectral Clustering with Flexible Extension

TPAMI.2022
Zhoumin Lu & Feiping Nie et al.

Abstract

与传统方法相比，深度学习方法是数据驱动的，有更大的搜索空间来寻找解决方案，这可能会找到更好的解决方案。此外，损失函数可以引入更多的考虑因素，因此深度模型是高度可重用的。然而，传统方法具有更好的可解释性，其优化相对稳定。

在本文中，我们结合传统方法和深度学习方法的优势，提出了一种多视图谱聚类模型。具体来说，我们从传统谱聚类的目标函数开始，进行多视图扩展，得到传统的优化过程。然后，通过对这一过程进行部分参数化，我们进一步设计了相应的可微模块，最终构建了一个完整的网络结构。该模型具有一定的可解释性和可扩展性。实验表明，该模型比其他多视图聚类算法性能更好，其半监督分类扩展也比其他算法具有优异的性能。进一步的实验也表明了模型训练的稳定性和较少的迭代。

Introduction

多视图学习侧重于从不同的角度发现共同的模式，这有助于提高性能。对于一个视频来说，它的文本、音频和图像可以被视为三个视角。对于图像，其颜色特征和纹理特征可以作为多个视角进行查看。对于一个文档来说，它来自多个来源的文本描述可以看作是几个角度。即使是各种降维方式和众多的图构建手段也可以被视为不同的视角。多视图聚类不仅是多视图学习的一个重要分支，也是单视图聚类的一个显著扩展。

近年来，深度聚类受到了极大的青睐。由于其较大的参数空间，可以搜索到良好的低维表示。由于它利用损失函数来指导学习，因此深度模型具有显著的可重用性。即便如此，传统聚类仍然具有很大的研究价值，受到许多领域的青睐。由于传统聚类具有显著的可解释性和理论支持，因此它的输出可靠性是有保证的。由于其优化方向保持相对固定，因此在训练过程中保持相对稳定，不易出现不可接受的情况.

在本文中，考虑到传统和深度学习方法的特点，我们提出了一种具有灵活扩展的多视点谱聚类模型。该模型以传统优化为基础，以部分参数化为手段，以网络结构为主体，以损失函数为指导，利用神经网络的优势，成为谱聚类的改进版本。这项工作的贡献总结如下：

1. 从多视图学习的角度出发，我们提出了一种新的多视图聚类模型。它也可以应用于只有一个额外损失函数的多视图半监督分类问题。理论和实验分析表明，我们的模型具有许多良好的财产：迭代次数少、训练更稳定、性能更好、标签依赖性更低等。此外，由于超参数少且不敏感，该模型可以更容易地用于不同的数据集。
2. 从模型重用的角度来看，通过简单地修改激活函数和/或损失函数，我们的模型还可以解决多视图聚类以外的问题，如半监督分类、非负矩阵分解、主成分分析、深度聚类等。由于其模块化性质，它可以很容易地嵌入到其他应用程序中。此外，模块化允许修改激活函数，而无需遍历整个模型。
3. 从可解释模型的角度来看，我们直接构建了一个透明模型，而不是解释一个黑盒。该模型建立在传统优化过程的基础上，因此是可以自然解释的。此外，我们还对局部参数化进行了多方面的理论分析，使每一步都有充分的依据。消融研究进一步证明了我们模型的合理性和有效性。

Method

所提出的方法分为五个部分：问题公式化、可微框架、损失函数、可扩展性和可解释性。

Formulation

非负谱聚类（对称谱聚类）可以写作以下形式：
$$\underset{F\ge 0}{\min }\Vert W-F{F}^{\top }{\Vert }_F^2$$

其中W为affinty graph，F为nxk维的聚类指示矩阵。这是一种轻松的子图划分形式，通常性能更好，但解决起来相对麻烦。可以重写如下对称谱聚类：

其中，G可以被看作nxk维的聚类中心矩阵。本质上，这是通过邻接关系的广义k-means，其性能通常低于前者，但求解相对容易。一个简单半谱聚类半k-means的折衷方案如下：

当$\lambda$项足够大，我们就接近了原始的非负谱聚类；而当$\lambda =0$时则为广义k-means。接下来我们把目标函数扩展到多视图：

每个视图的聚类中心不一致但子图划分应当是一致的。${\lambda }_i$为第i个视图下的权重

Differentiable Framework

首先我们先不考虑非负约束，上式改写为

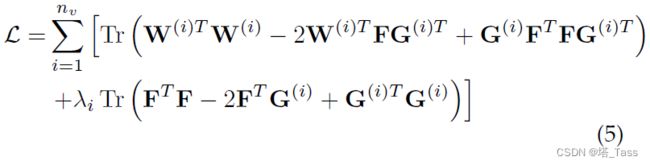
对$G^i$求偏导得到：

在无约束情况下求解到的$G^{(i)}$为：

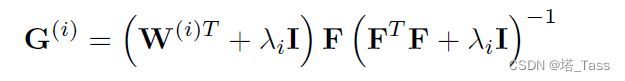
然后我们利用ReLU让$G^{(i)}\ge 0$:

我们把其中的$(W^{(i)\top }+{\lambda }_{i}I)F$项重参数化为$U^{(i)}$，那么第k次迭代规则为：

基于以上公式，我们搭建了一个 single inversion layer：

该模块用于从$F_{k-1}$推断$G_k^{(i)}$。

我们接下来对F求偏导：

得到无非负约束下的F的解：

同样地，我们用ReLU对F施加非负约束。类似地，我们再把${\sum }_{i=1}^{n_v}(W^i+{\lambda }_{i}I)G^{(i)}$项重参数化为$V$：

再构建一个ensemble inversion layer，把多个视图合并起来：

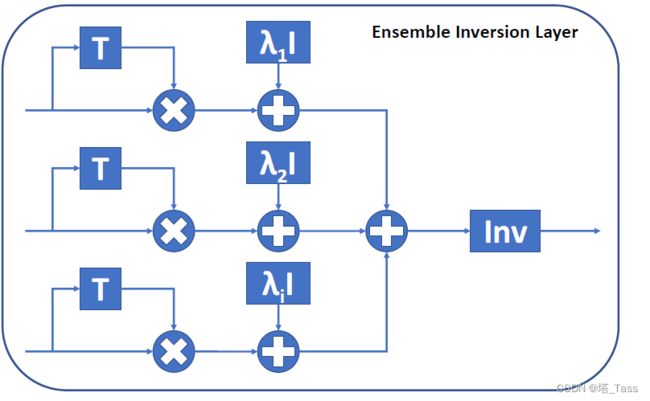
可以构建完整的网络结构，如下图所示。需要指出的是，${\lambda }_i$也是一个可学习的参数。

Loss function

考虑到每个视图都应该适合其相应的图结构，因此存在L1损失：

另一方面，共享的indicator矩阵应该适合包含所有视图信息的图结构，因此存在L2损失：

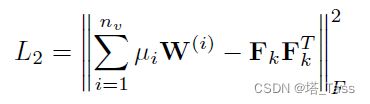
总损失函数为：
$$L_{cls}=L_1+\alpha L_2$$

在$L_2$中，$\mu$用于给不同视图分配权重，利用参考文献的定义：

Chandler Davis and William Morton Kahan. The rotation of eigenvectors by a perturbation. iii. SIAM Journal on Numerical Analysis.

略

Flexible extentions

I) 半监督分类

对于半监督分类，需要在聚类时分配正确的标签。因此，正确的聚类指示符矩阵F应该近似于经验估计的$F_{emp}$。存在L3损失:

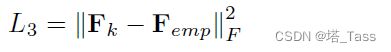
重新排列样本顺序，使有标签的样本排在第一位，即有：

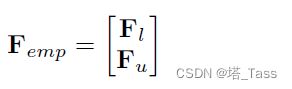
其中$F_l$和$F_u$分别是标记样本和未标记样本的聚类指示矩阵。虽然很常见，但将未标记的部分视为0是不合理的。此外，我们知道以下关系成立:

于是有：

所以$F_u$可以由$F_l$估计：

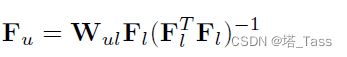
II) 非负矩阵分解

当只有单视图时，我们的损失函数退化为：

这显然是一个对称的非负矩阵分解问题，其中$a=1$。不失一般性地，我们把$W$替代为$X$，不考虑对称性，上述损失函数可以改写为：

这正是非对称的非负矩阵分解。如果需要保持流形，可以采用以下损失函数：

这是图规范化的非负矩阵分解。此外，NMF的一种分级变体被广泛认可，并通过以下损失函数学习：

在这里，每个block操作都被视为分解而不是迭代。这个想法是可行的，因为由于局部参数化，F和G的更新规则不依赖于X。

III) Principal Component Analysis

原始主成分分析方法如下：

因此我们可以通过放松写成如下形式：

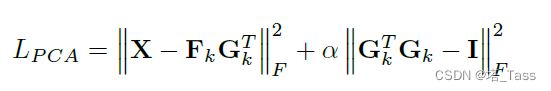
其中$\alpha$应当设置得足够大。我们可以通过设置F和G的激活函数来调整约束。例如非负时为$ReLU(x)$，稀疏时为$sgn(x)(x-\theta {)}_{+}$，无约束时等于输入$x$本身。

可解释性

与传统的优化算法相比，深度学习模型往往具有更好的性能。但深度学习通常很难解释，这极大地限制了对结果的可靠性评估。尽管许多工作通过设计实验或可视化中间过程来帮助理解网络，但许多领域仍然倾向于采用传统模型。这是因为深度模型的网络结构是一个复杂的非凸映射，导致训练不稳定。相反，为了稳定输出，我们提出了一系列额外的操作来进一步增加网络复杂性。与解释黑盒不同，我们使用传统的优化算法来构建网络结构。这样的网络自然是可解释的，并缩小了解决方案的搜索范围，以确保优化的正确方向。由于更新规则是部分参数化的，因此可以通过各种损失函数更灵活地学习，这被称为基于学习的优化。这相当于在传统优化中增加了计算扰动，从而扩大了解的搜索范围。

本质上，我们的方法像传统方法一样搜索收敛序列$\{F_t\}$。因此，数据通过一个block传播，类似于传统优化中的一次迭代。在传统的优化中，$\{F_t\}$一旦确定就不会改变，并且序列长度是未知的。在基于学习的优化中，序列长度固定为block的数量，并且可以更新$\{F_t\}$。

复杂度

在只重参数化为U在正向/反向传播的计算复杂度为$\mathcal{O}(n{k}^2)$，重参数化V后在正向/反向传播的计算复杂度为$\mathcal{O}(n^{2}k)$

实验

数据集

settings

在多视图聚类和分类中，我们的方法在每个数据集上都保留了相同的设置。具体地，块的数量被设置为5，并且初始值被设置为20。平衡系数$\alpha =1$和$\beta =3$。初始学习率设置为0:3，学习率每两个epoch衰减一次，衰减率为0.99。完整的训练需要使用Adam进行500个epoch。

performance

无监督聚类

10% label半监督分类

消融实验