舌体胖瘦的自动分析-曲线拟合-或许是最简单判断舌形的方案（六）

返回至系列文章导航博客

1 简介

在中医智能舌诊项目中需要舌体胖瘦的自动分析
舌体胖瘦是中医诊断中重要的观察依据，。胖大舌“舌色淡白，舌体胖嫩，比正常舌大而厚，甚至充满口腔”，主脾肾阳虚，气化失常，水湿内停。舌体比正常舌瘦小而薄，称为“瘦薄舌”，主气血两虚和阴血不足。中医一般通过与正常舌比较来判断舌的胖瘦。但由于年龄、性别、区域的差异，正常舌本身就没有一个大小标准，给舌体胖瘦的自动定量分析造成困难。并且由于用户上传的图像比例差异比较大，这使得舌形判断难上加难。

在进行舌体胖瘦判断应有两个前提：

（1）用户上传的舌象图片已经被分割完成；

（2）舌体处于“垂直状态”；

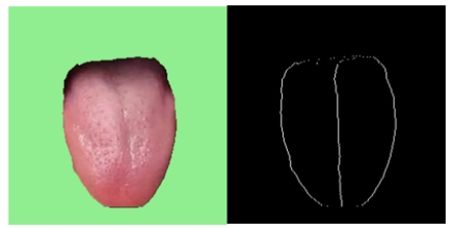
这两个步骤的处理方案已在之前的文章中有所介绍：
【python-Unet】计算机视觉 舌象舌头图片分割 机器学习（三）
【python】计算机视觉~舌象图片中舌体倾斜判别（四）

下面我们来详细讲解如何让计算机智能判别用户上传的舌象胖瘦！

2 原理讲解——多项式曲线拟合

2.1 舌体曲线拟合参数与形状的关系

通过对舌体轮廓进行曲线拟合，可以用较少的参数表示舌体轮廓。对舌前部轮廓采用4次多项式拟合

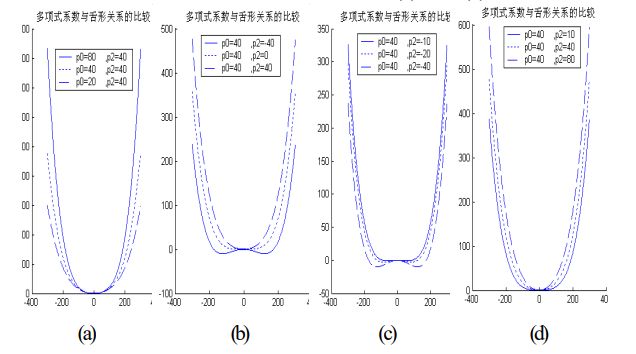
发现曲线拟合参数与曲线形状的尖锐与圆钝有以下关系：
（1）由于舌体接近对称，因此奇次项系数一般相对较小，对舌体形状的影响较小，而常数项根本不影响曲线的形状。
（2）舌体的总体形状趋势取决于其最高项——四次项，在其他各项系数相同的情况下，四次项系数越大，曲线越尖锐；越小，曲线越圆钝。
（3）尖锐和圆钝的程度不但与四次项和二次项的符号关系有关，还与两个系数的绝对值关系有关。二次项与四次项系数绝对值之比越大，曲线的尖锐与圆钝越显著。

2.2 胖瘦指数定义

通过上述函数图像的特点总结胖瘦指数。
胖瘦指数与四次项系数绝对值成反比，并且与二次项系数和四次项系数的符号关系和绝对值之比有关。胖瘦指数越大，舌体越胖。根据胖瘦特征已知的舌图像样本确定分级标准，可以将舌体描述为“胖”、“不胖不瘦”、“瘦”3种类型。

其中a4为四次项系数，a2为二次项系数。

3 具体实现过程

首先是要将舌象图片进行舌体分割（参照【python-Unet】计算机视觉 舌象舌头图片分割 机器学习（三））

舌体胖瘦分析的主要的对象是中下舌位，上舌位会影响分析的准确性，因此取舌体轮廓标记点的下0.75舌位。示意图如下图所示：

对下0.75舌位标记像素点进行舌体轮廓的多项式曲线拟合。由于分析的是曲线的“胖瘦”，因此多项式曲线的奇数次项影响较小，且项数较大较好。权衡模型的运行效率，中e诊采用4次项多项式曲线拟合。进行多张图片拟合的确定系数（R-square=SSR/SST）为0.82~0.95，说明4次多项式曲线拟合效果较好。舌体轮廓4次多项式拟合示意图如下：

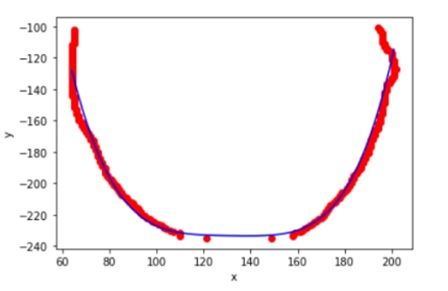
将得到4次多项式拟合曲线系数代入如下公式，计算胖瘦指数。通过胖瘦指数来判断用户舌体的胖瘦。

其中a4为四次项系数，a2为二次项系数。
胖瘦值数越大说明舌体越宽大，胖瘦指数越小说明舌体越瘦小；胖瘦指数位于4.3-7.8范围内是正常舌，小于4.3是瘦小舌，大于7.8是肥大舌。
注：这里的数据可能准确度并不高，应当在大量样本数据验证后得出结论，需要后面继续验证！

4 代码实现

注：此后的代码是在已经分割好舌象以及舌体倾斜判断后，其中代码参照前文！

4.1 contour_to.py

from PIL import Image
import numpy as np

def contour_to(in_path=r"result\blend.png", out_path=r"result\inline.png"):
    """
    将分隔好的图像数据进行描点
    in_path为绿底+原图图片
    put_path为黑底+白点图片
    返回对称轴坐标以及轮廓坐标
    """
    img_before = Image.open(in_path)
    img_before_array = np.array(img_before)  #把图像转成数组格式img = np.asarray(image)

    shape_before = img_before_array.shape
    
    height = shape_before[0]
    width = shape_before[1]
    dst = np.zeros((height,width,3))
    
    wire = []
    axle_wire = []
    outcome_wire = []
    

    for h in range(0,height):
        lis = []
        h_all = 0
        w_all = 0
        for w in range (0,width-1):
            (b1,g1,r1) = img_before_array[h,w]
            (b2,g2,r2) = img_before_array[h,w+1]
            if (b1, g1, r1) == (1,204,182) and (b2,g2,r2) != (1,204,182): 
                dst[h, w] = (255,255,255)
                lis.append((h,w))
                outcome_wire.append((h,w))
            elif (b1, g1, r1) != (1,204,182) and (b2,g2,r2) == (1,204,182):
                dst[h, w+1] = (255,255,255)
                lis.append((h,w+1))
                outcome_wire.append((h,w+1))
            else:
                pass

        if len(lis) == 0:
            pass
        else:
            for i in lis:
                h_all += i[0]
                w_all += i[1]
            h_avg = h_all//len(lis)
            w_avg = w_all//len(lis)
            dst[h_avg, w_avg] = (255,255,255)
            axle_wire.append((h_avg, w_avg))

    img2 = Image.fromarray(np.uint8(dst))
    img2.save(out_path,"png")
    
    wire.append(axle_wire)
    wire.append(outcome_wire)
    
    return wire

4.2 outline_cut.py

import numpy as np 
from PIL import Image

def outline_cut(outcome_wire):
    """
    截取轮廓下1/4像素点
    """
    save = outcome_wire
    pool = []
    for i in outcome_wire:
        pool.append(i[0])
    pool.sort()
    judge = pool[int(1 + (float(len(pool)) - 1) * 1 / 4)]
    
    

    del_data = 0
    for i in range(len(outcome_wire)):
        if outcome_wire[i][0] < judge:
            del_data = i
        else:
            pass

    del save[0:del_data]
    
    height = 256
    width = 256
    dst = np.zeros((height,width,3))
    for i in outcome_wire:
        h = i[0]
        w = i[1]
        dst[h,w] = (255,255,255)
    img2 = Image.fromarray(np.uint8(dst))
    img2.save(r"result\0.5cuted.png","png")
    
    return save

4.3 linger.py

import matplotlib.pyplot as plt
import numpy as np
from sklearn import  linear_model
#导入线性模型和多项式特征构造模块
from sklearn.preprocessing import  PolynomialFeatures

def linger(wire):
    a1, a2 = zip(*wire)
    x = list(a2)
    y = list(map(lambda i: i * -1, a1))
    datasets_X = x
    datasets_Y = y

    #求得datasets_X的长度，即为数据的总数。
    length =len(datasets_X)
    #将datasets_X转化为数组， 并变为二维，以符合线性回 归拟合函数输入参数要求
    datasets_X= np.array(datasets_X).reshape([length,1])
    #将datasets_Y转化为数组
    datasets_Y=np.array(datasets_Y)

    minX =min(datasets_X)
    maxX =max(datasets_X)
    #以数据datasets_X的最大值和最小值为范围，建立等差数列，方便后续画图。
    X=np.arange(minX,maxX).reshape([-1,1])
    #degree=4表示建立datasets_X的四次多项式特征X_poly。
    poly_reg =PolynomialFeatures(degree=4)
    X_ploy =poly_reg.fit_transform(datasets_X)
    lin_reg_2=linear_model.LinearRegression()
    lin_reg_2.fit(X_ploy,datasets_Y)

    #查看回归方程系数
    #print('Cofficients:',lin_reg_2.coef_)
    #查看回归方程截距
    #print('intercept',lin_reg_2.intercept_)
    plt.scatter(datasets_X,datasets_Y,color='red')
    plt.plot(X,lin_reg_2.predict(poly_reg.fit_transform(X)),color='blue')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
    return lin_reg_2.coef_

4.4 调用总函数

coefficient = linger.linger(contour_to.outline_cut(contour_to()[1]))
print(coefficient)

后根据coefficient中的多项式系数代入如下公式判断舌体胖瘦：

舌体判别算法至此结束

总的来讲就是：
step1：舌象图片自适应调节
step2：舌体分割
step3：舌体倾斜判断
step4：曲线拟合判断舌形