一些算法知识整理

最近找工作，整理了一些算法知识，希望能帮助到同样在找工作的同学。

1、LR：

逻辑回归，用于分类问题，模型可以理解为 线性模型+sigmoid函数：$$y=\frac{1}{1+e^{-(wx+b)}}$$
其优化目标是最大化对数似然函数：
$$l(w,b)=\sum _{i=1}^{m}lnp(y_i|x_i;w,b)$$
逻辑回归和线性回归的最本质的区别就是逻辑回归是分类问题，线性回归是回归问题，逻辑回归的因变量y服从二元分布，线性回归的因变量y在使用最小二乘法求解时服从正态分布。

逻辑回归处理多分类问题：多项式逻辑回归，或者训练多个二分类模型（样本处理成是第i类和非第i类），或者使用softmax函数。

2、SVM：

SVM本质上是要找到一个超平面使得两个不同类的支持向量到超平面的距离之和$\gamma =\frac{2}{||w||}$。$\gamma$被称之为“间隔”。SVM的目标就是最大化此间隔。
$$\{\begin{array}{l}\underset{w,b}{\min }\frac{1}{2}||w|{|}^2\\ s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2,...,m\end{array}$$

模型的求解是一个凸优化的问题，每一项加入一个拉格朗日乘子：
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))$$

KKT条件约束：
$$\{\begin{array}{l}{\alpha }_i\ge 0\\ y_i(w^T{x}_i+b)-1\ge 0\\ {\alpha }_i(y_i(w^T{x}_i+b)-1)=0\end{array}$$

目标函数的求解算法SMO：其思路是①选取一对需要更新的变量${\alpha }_i$和${\alpha }_j$；②固定${\alpha }_i$和${\alpha }_j$以外的参数，然后进行优化更新；③一直重复以上两个步骤直到收敛。SMO采用启发式选取两个变量，使选取的两个变量对应样本之间的间隔最大，原因是这样的两个变量有很大差别，与对两个相似的变量进行更新相比，对它们进行更新会带给目标函数值更大的变化。

核函数是解决原始样本线性不可分的问题，将原始样本映射到更高维度，使得样本可分。常用的核函数：线性核函数；多项式核函数；高斯核函数；拉普拉斯核函数；Sigmoid核函数。

3、K-Means：

K-Means聚类属于无监督学习，将给定样本划分k类$C=\{C_1,C_2,...,C_k\}$，模型目标:
$$E=\sum _{i=1}^k\sum _{x\in C_i}||x-{\mu }_i|{|}_2^2$$
其中${\mu }_i=\frac{1}{C_i}{\sum }_{x\in C_i}x$是类别$C_i$的均值向量。这是一个NP难问题，因此，K-Means采用了贪心策略，通过迭代优化来近似求解。

策略思想就是：①首先初始化k个类别的均值$\mu$（即：随机选择K个样本）；②计算各样本$x$和$\mu$的距离，来确定样本的类别；③根据样本的类别重新计算类别的均值$\mu$；④重复2、3步骤直到类别均值$\mu$不再更新。

聚类算法还有：①密度聚类；②高斯混合聚类；③层次聚类；

4、决策树：

决策树主要分两种：分类树和回归树。
分类树的生成有信息熵和基尼系数两种算法，
信息熵可以度量样本的纯度，如样本D中第i类样本所占的比例$p_i$，则样本D的信息熵
$$Ent(D)=\sum _{i=1}^K{p}_{i}lo{g}_2{p}_i$$

熵越小，纯度越高。而节点划分是一个信息增益的过程：
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$

其中$D^v$表示第v个分支节点包含了D中所有属性a上取值为$a^v$的样本。
信息增益越大，则意味着使用属性a来进行划分所得的“纯度提升”越大。

最大化$Gain(D,a)$

基尼系数反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。
$$Gini(D)=\sum _{k=1}^K\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}=1-\sum _{k=1}^K{p}_k^2$$

所以，基尼系数越小，表示纯度越高。
则划分属性a的基尼系数为：
$$Gini(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$

最小化$Gini(D,a)$

为什么有了信息熵，还需要基尼系数？原因是信息熵的计算比基尼系数的计算更加复杂（需要计算每个类别的对数），大规模数据集下，耗时更多；还有在类别不平衡的情况下，基尼系数更加准确，基尼系数的计算更加注重类别的概率。

回归树的输出y是一个连续变量，所以它是一个回归问题，使用平方误差来划分节点，算法思路：选择第j个变量$x_j$和它的取值s作为切分变量和切分点，然后定义两个区域：
$$R_1(j,s)=\{x|x_j\le s\}和R_2(j,s)=\{x|x_j>s\}$$

然后使用
$$\underset{j,s}{\min }[\underset{{\mu }_1}{\min }\sum _{x_i\in R_1(j,s)}(y_i-{\mu }_1{)}^2+\underset{{\mu }_2}{\min }\sum _{x_i\in R_2(j,s)}(y_i-{\mu }_2{)}^2]$$

其中${\mu }_1$和${\mu }_2$是$R_1(j,s)$和$R_2(j,s)$中y变量的均值。

5、树的相关处理：

剪枝是决策树处理过拟合的一个主要手段，主要有“预剪枝”和“后剪枝”两种策略。
预剪枝是在决策树生成的过程中，对每个节点在划分前进行估计，若当前节点的划分不能带来决策树泛化性能提升，则停止划分，并将当前节点标记为叶节点。此方法不仅可以防止过拟合，还能减少决策树的训练时间和开销，但也可能带来欠拟合。
后剪枝则是先生成一颗完整的决策树，然后自底向上地对非叶节点进行估计，若将该节点对应的子树替换为叶节点能带来决策树泛化性能提升，则将该子树替换为叶节点。该策略增加了决策树的训练时间和开销。
连续值处理一般采用二分法。

树的集成算法：

Bagging：可以并行训练，每次训练随机有放回抽取样本训练，最后综合所有模型的结果。
Boosting：串行训练，每次训练会拟合上一次训练的预测结果，并且每次训练会根据预测结果给样本分配权重，使预测结果不好的样本下次训练被抽取的概率更高。
Stacking：分层训练，先使用原数据集训练，得到多个弱学习器，然后将预测结果作为新特征构造新数据集，最后使用新数据集训练得到最终的模型。

6、集成学习的偏差和方差：

偏差反映了预测值和真实值之间的距离（偏差小，精确度高），即拟合程度。
方差反映了预测值作为随机变量的离散程度（方差大，过拟合，没有泛化性），即泛化程度。
弱模型指的是偏差高（在训练集上准确度低）方差小（防止过拟合能力强）的模型，集成学习中只有Boosting中的基模型是弱模型（偏差高，方差低），Bagging和Stacking中的基模型是强模型（偏差低，方差高）。

在Bagging中，为什么基模型是强模型，整体模型会比基模型效果好？
因为整体模型的准确度是由偏差和方差共同决定，而整体模型的偏差和基模型的篇近似（因为基模型是强模型，整体模型的期望和基模型的期望相等，这也是为什么Bagging的基模型必须要是强模型），整体模型的方差要小于等于基模型的方差，并且随着基模型的数量增多，方差减小。当基模型数增加到一定程度时，方差的减小会到达一个极限，即整体模型的防过拟合能力达到极限。
Random Forest是经典的基于Bagging 框架的模型，并在此基础上通过引入特征采样和样本采样来降低基模型间的相关性，从而更好的提升模型的防过拟合能力。

在Boosting中的基模型是强相关性，整体模型的方差等于基模型的方差，即整体模型的防过拟合能力和基模型近似（这也是为什么Boosting中的基模型必须是弱模型，如果方差较大则整体模型无法达到防止过拟合）。Boosting采用基于贪心策略的前向加法，整体模型的准确度随着基模型的数量增加而逐渐提高。

AdaBoost：自适应增强，每一轮训练中被基模型预测出错的样本会得到加强，从而在下一轮训练中更容易被抽取到。最后所有基模型都会赋予的权重，最终模型的预测结果是基模型加权计算的结果。

7、GBDT：

GBDT是一个基于boosting算法的梯度提升树模型。它的基模型是回归树，每次训练都是基于前一次训练的预测结果的残差更新目标，因此GBDT模型的结果是所有基模型累加和：
$${\hat{y}}_i=\sum _{k=1}^K{f}_k(x_i)$$

每次训练的基模型为：
$${\hat{y}}_i^{(k)}={\hat{y}}_i^{(k-1)}+f_k(x_i)$$
GBDT中的梯度提升主要体现在每次训练时的残差，因为根据目标求解，这里的残差其实就是最小均方损失函数关于预测值的反向梯度
$$-\frac{\partial (\frac{1}{2}(y-{\hat{y}}_i^{(k)}{)}^2)}{\partial {\hat{y}}_i^{(k)}}=y-{\hat{y}}_i^{(k)}$$
即：预测值和真实值的残差于损失函数的负梯度相同。
【注】基于残差的GBDT对异常值很敏感，所以一般回归类的损失函数会用绝对损失或者Huber损失函数替代平方损失函数。
绝对损失函数：
$$L(y,F)=|y-F|$$
HUber损失函数：
$$L(y,F)=\{\begin{array}{l}\frac{1}{2}(y-F{)}^2|y-F|\le \delta \\ \delta (|y-F|-\delta /2)|y-F|>\delta \end{array}$$
GBDT每次训练残差的计算相当于增大了被预测出错的样本权重。

缩减策略（shrinkage）：shrinkage思路：没走一小步逐渐逼近结果的效果要比每次一大步逼近结果的方式更容易避免过拟合，所以对残差附加了一个权重：
$${\hat{y}}_i^{(k)}={\hat{y}}_i^{(k-1)}+\mu f_k(x_i)(0<\mu \le 1)$$
shrinkage不直接用残差修复误差，而是把大步分成小步，本质上shrinkage为每棵树设置了一个weight，累加时要乘以这个weight，当weight降低时，基模型会配合增大。

AdaBoost和GBDT的区别：迭代思路不同，AdaBoost是通过提升错分样本的权重来弥补模型的不足，GBDT通过残差弥补模型的不足；损失函数不同，AdaBoost使用指数损失，GBDT使用绝对损失或者Huber损失。

8、XGBoost：

XGBoost是基于boosting算法的集成树模型，每一棵树是一个弱分类器，所有弱分类器集成后，形成强分类器。
$$\widehat{y_i}=\sum _{k=1}^K{f}_k(x_i)$$
其中$f_k(x_i)$是一个基于CART树的弱分类器。而弱分类器的训练都要拟合上一次训练得到的弱分类器预测的残差，即当生成k棵树的预测值为：
$${\hat{y}}_i^{(k)}={\hat{y}}_i^{(k-1)}+f_k(x_i)$$
XGBoost的目标函数：
$$L(\varphi )=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i)+\sum _{k=1}^K\Omega (f_k),\Omega (f_k)=\gamma T+\frac{1}{2}\lambda ||\omega |{|}^2$$

其中$l$函数一般使用MSE来衡量，$T$表示叶子节点的个数，$\omega$表示叶子节点的分数。$\gamma$可以控制叶子节点的个数，$\lambda$可以制叶子节点的分数不会过大，防止过拟合。 XGBoost的梯度提升体现在每训练一棵树都要拟合上一棵树的残差，而目标函数的优化采用泰勒二次项展开。
XGBoost采用了shrinkage和特征抽样策略防止模型过拟合，
XGBoost的分支（level-wise）策略：
1、精准的贪婪算法，首先对特征进行排序，然后对所有的特征进行遍历，并计算特征所有划分的可能。该方法的优点是精确度很高，但是计算耗时，不适合大数据集。
2、近似算法：首先根据特征分布的百分位数选出候选分支点，然后将连续特征映射到候选点划分的桶中对统计量进行聚合，并根据这个聚合统计量从中找到最优划分点。
3、Sparsity-aware Split Finding：处理确实特征的分支算法，一是默认将其划分到一边，二是从没有缺失的样本中学习特征的分支方向。
XGBoost的缺点：回归树分支预排序的开销太大，训练速度耗时，对内存空间要求高。level-wise的建树算法可以很好的进行并行计算，从而加速预排序算法，但是效率低，没必要分支的节点也进行了分支。

9、LightGBM：

LightGBM可说是在XGBoost的基础上改进优化的一个基于boosting的模型，LightGBM在建树的过程中采用了基于直方图的算法，对特征进行分箱，这带来的优势是降低了计算的时间复杂度，加快了训练速度，降低了对异常值的敏感，鲁棒性更好。缺点就是找出的分支点没有GBDT精确。
生成树的方式采用带深度限制的leaf-wise策略。leaf-wise找到所有叶子节点中增益最大的节点进行分裂（对于右节点则直接使用父节点和左节点的信息直接计算），其优点是在分支次数相同的情况下可以降低更多的误差，从而得到更好的精读。但也容易过拟合，因此增加了树的最大深度加以限制，从而防止过拟合。
基于梯度的单边采样算法，训练过程中，如果一个样本与小梯度关联，那么说明这个样本的训练误差已经很小了，没必要训练了。因此算法根据样本的梯度保留梯度值大的样本，对小梯度样本随机抽样，保证整个训练集的样本分布。该算法减少了样本维度，加快了模型的训练速度。
互斥特征捆绑，将数据集中互斥的特征捆绑在一起组成新的特征（特征组合）。具体思路：①构建一个以特征为顶点，带权重图，权重为特征同时不为零的样本的个数；②根据顶点的度对特征进行降序排序，度越大表示特征与其他特征的冲突越大，则越不可能与其他特征进行捆绑；③设置最大冲突阈值k，遍历排序好的特征，如果发现特征加入已有特征簇的冲突数小于最大阈值k，则将该特征加入到该特征簇，否则新建一个特征簇。该算法减少了特征维度，加快了模型的训练。
LightGBM训练加速总结：
1、data sub-sampling，对数据集采样；
2、feature sum-sampling，对特征采样；
3、支持类别特征，无需one-hot编码；
4、保存数据文件为二进制文件，提高特征的加载速度；
5、并行学习，支持特征并行，数据并行，结果投票并行；
LightGBM如何避免过拟合：
1、特征直方图分桶；
2、单棵树不要太复杂，使用更小的num_leaves；
3、确保叶子节点有足够多的数据，控制min_data_in_leaf和min_sum_hessian_in_leaf参数；
4、训练每棵树时对数据集进行采样，设置bagging_fraction参数；
5、训练每棵树时对特征进行采样，设置feature_fraction参数；
6、控制树的最大深度，设置max_depth参数；
7、使用正则化；

10、DeepFM：

DeepFM模型是DNN和FM的结合，DNN负责特征深度交互的一个学习，FM负责特征浅层交互的一个学习。
FM在逻辑回归的基础上加入特征两两交互的二阶项：
$$\hat{y}=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^{n-1}\sum _{j=i+1}^n{w}_{ij}{x}_i{x}_j$$

其中$w_{ij}$表示特征对应特征组合的权重，这个参数按上式比较难更新，因为对于经过one-hot编码的特征可能比较稀疏，特征交互之后很可能变成0，导致$w_{ij}$得不到更新。
解决方法是对特征$x_i$引入k维辅助向量$v_i=(v_{i1},v_{i2},...,v_{ik})$，原来的组合权重$w_{ij}$可以表示为$v_j{v}_j^T$，FM模型可以表示为：
$$\hat{y}=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^{n-1}\sum _{j=i+1}^n⟨v_i,v_j⟩x_i{x}_j$$

通过这种转换，特征交互项的参数由$n(n-1)/2$个减少到$n\times k$个，大大降低了模型的复杂度。
FM虽然加入了特征交互，但从公式中可以看出特征和不同特征交互共用一组参数，不能表达出特征和不同特征交互的不同，所以表达能力非常有限，不及深度学习模型。
DeepFM的模型结构如下图，由FM Layer和Hidden Layer组成，稀疏特征进行one-hot编码，进入Dense Embedding得到特征的稠密向量，FM Layer的输入是一阶的稀疏特征+二阶的稠密特征，Hidden Layer的输入是稠密特征，最后Output Units是将FM Layer的输出和Hidden Layer的输出拼接作为输入过Sigmoid函数。

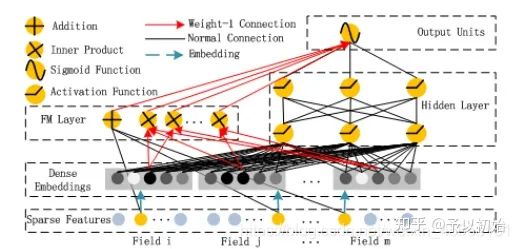
DeepFM的优点：直接端对端训练，无需人工选择特征和特征交互。

【面试题】FM 本来就可以在稀疏输入的场景中进行学习，为什么要跟 Deep 共享稠密输入？
共享稠密输入是FM的二阶项，虽然FM可以在稀疏输入的场景中学习，但是one-hot编码的高维输入比稠密低维输入带来数量级的计算量。所以共享稠密输入可以降低计算量，从而提高训练速度。

11、DCN：

DCN模型是在DNN的基础上加入了特征的交叉项，如下图左边的cross network。cross network有点类似fm，不同于fm的地方就是可以通过网络层数构造不阶的特征交互。每一层的网络模型公式：
$$x_{l+1}=x_0{x}_l^T{w}_l+b_l+x_l=f(x_l,w_l,b_l)$$

一层输出：
$$x_1=x_0{x}_0^T{w}_0+b_0+x_0$$

二层输出：
$$x_2=x_0{x}_1^T{w}_1+b_1+x_1$$

12、DIN：

DIN(Deep Interest Network，深度兴趣网络)，通过引入注意力机制来更精准地捕获用户的兴趣，网络结构如下图：

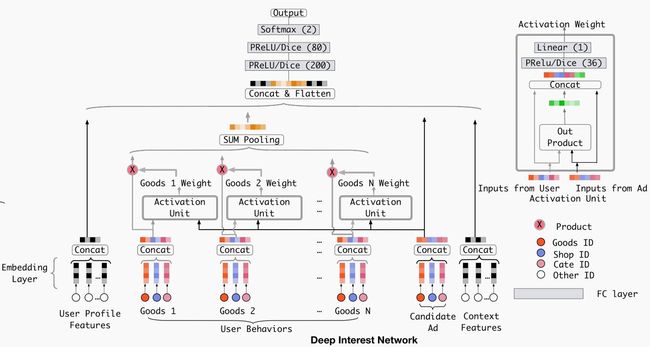
模型包含Embedding Layer、Activation Unit以及MLP。
Embedding Layer使用的group-wise方法进行特征表示，为什么使用group-wise，大概是因为不同的group使用的编码规则不一样，如User Behavior Features使用multi-hot编码，其他特征使用one-hot编码，并且不同group中的ids特征可能重复导致不同group的特征编码一致。
Activation Unit是一个pay attention to locally activate interests 单元，主要思想是用户当前的行为兴趣对用户的兴趣建模非常重要（即：和用户行为兴趣相关的展示内容更容易被点击）。该单元主要计算不同候选item和用户行为的权重，因此，可以学习到用户行为和不同item的一个向量表示，该单元的模型：
$$v_U(A)=f(v_A,e_1,e_2,...,e_H)=\sum _{j=1}^{H}a(e_j,v_A)e_j=\sum _{j=1}^H{w}_j{e}_j$$

其中$v_U(A)$用户被给候选item A时的向量表示，$e_1,e_2,...,e_H$表示用户的行为向量，$v_A$表示候选item A，$a(\cdot )$一个前向反馈网络，输出activation weight，如上图右边所示。
这里的注意力机制和NLP中的attention机制不同，这里的权重和${\sum }_{j=1}^H{w}_j$没有限制它一定要等于1，这样更有利于保留不同item得到的embedding的差异。
MLP一个常规的深度网络，将所有用户特征和activation unit的输出以及内容特征concat作为输入，最后经过softmax输出。
模型训练的两个优化：
mini-batch aware正则主要是解决大规模稀疏场景下SGD对引入L2-norm正则的loss更新计算开销过大的问题，L2-norm正则会计算每个batch中的所有特征参数，而mini-batch aware正则只计算小批量中稀疏特征的参数，可以得到一个近似的L2-Norm的结果。
自适应激活函数该激活函数是基于PReLU改进的，PReLU函数为：
$$f(s)=\{\begin{array}{l}ss>0\\ \alpha ss\le 0\end{array}=p(s)\cdot s+(1-p(s))\cdot \alpha s,p(s)=I(s>0)$$

PReLU激活函数的控制函数$I(s>0)$当值为0时很难调整，这不适合每层有不同分布的输入。考虑到这一点，设计了Data Adaptive Activation Function，具体公式如下：
$$f(x)=p(s)\cdot s+(1-p(s))\cdot \alpha s,p(s)=\frac{1}{1+e^{-\frac{s-E[s]}{\sqrt{Var[s]+ϵ}}}}$$

其中$E[s]$和$Var[s]$分别表示期望和方差，$ϵ$是一个特别小的常数。

13、MMoE：

模型框架如下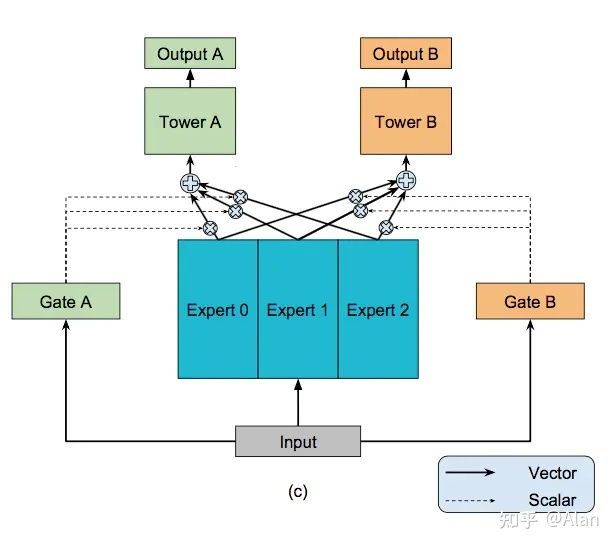
模型主要有门控和专家网络组成，每个任务一个门控，输出权重，不同任务赋予专家网络的输出不同的权重，然后再输入到各自任务的Tower网络。

14、DSSM：

双塔模型：详情参见这里

15、DMTL：

由MMoE和DSSM模型组成，蒸馏学习方法，利用DSSM模型学习user和item的embedding表示，通过KL loss配合MMoE模型学习多任务。模型结构如图，详情参见这里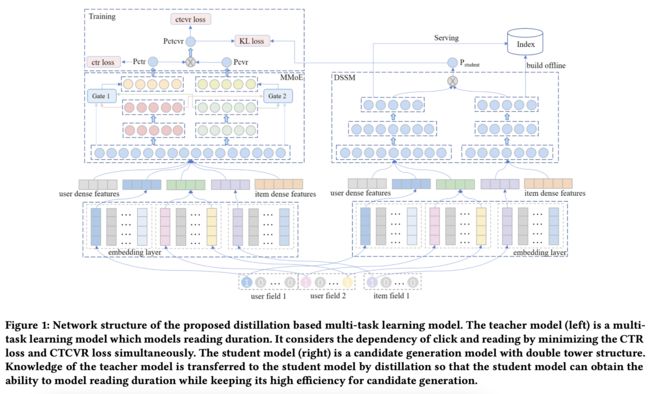

16、ESMM：

ESMM模型是一个多目标学习模型，解决的是CVR的问题，但是CVR预估存在两个关键问题：
1、Sample Selection Bias（SSB），转化问题是从CTR->CVR的过程，传统模型使用点击并转化的样本为正样本，点击没有转化的样本为负样本。然而，在线上预估的时候用的确实全样本曝光样本，训练和预测存在偏差，对模型的泛化构成很大的挑战。
2、Data Sparsity（DS），传统模型使用点击样本作为训练集，点击->转化在全样本中是非常稀疏的。
本文用于CVR的预估建模：
$$pCVR=p(z=1|y=1,x)$$

其中$z$表示转化，$y$表示点击，$x$是输入样本。关联概率：点击率($pCTR=p(y=1|x)$)和点击转化率($pCTCVR=p(y=1,z=1|x)$)，根据条件概率公式，可以得到：
$$p(y=1,z=1|x)=p(y=1|x)\times p(z=1|y=1,x)$$

以上就是ESMM建模思想。

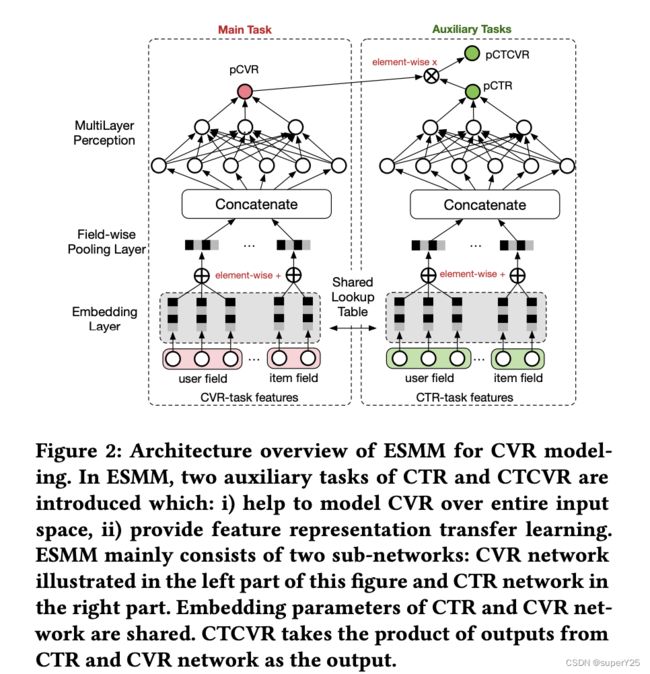
如上图是ESMM模型框架，主要两部分CVR任务和CTR任务。两个任务的Embedding Layer共享参数，到多层感知机层各自训练自己的参数，模型最终的目标函数：
$$L({\theta }_{cvr},{\theta }_{ctr})=\sum _{i=1}^{N}l(y_i,f(x_i;{\theta }_{ctr}))+\sum _{i=1}^{N}l(y_i\&z_i,f(x_i;{\theta }_{ctr})\times f(x_i;{\theta }_{cvr}))$$

其中$l(\cdot )$表示交叉熵损失函数。模型使用的训练数据是全空间的曝光数据集。

17、DBMTL：

DBMTL模型是基于贝叶斯算法构建的多任务学习模型，网络结构：
主要有共享Embedding层、共享MLP、单任务的MLP以及贝叶斯层。

DeepWalk：

DeepWalk模型主要用于图节点的语义表示，思路是通过随机游走获取节点的局部序列信息，然后使用Skip-gram模型训练得到节点的向量表示。
涉及到的几个参数：$w$Skip-gram的滑动窗口大小，$d$输出向量的维度，$\gamma$每个顶点游走几次，$t$每次游走几步。
DeepWalk的缺点：因为节点的序列是靠完全随机游走得到的，没有任何其他信息，所以只能反映相邻节点之间的社区相似信息，无法学习到节点的属性和边的信息。

18、Node2Vec：

Node2Vec模型和DeepWalk的思路相似，只是将游走算法由一阶随机游走替换成了二阶的有偏游走，不仅与当前节点有关，还和上一个节点有关。根据参数p和q的设置主要有深度优先（DFS）和广度优先(BFS)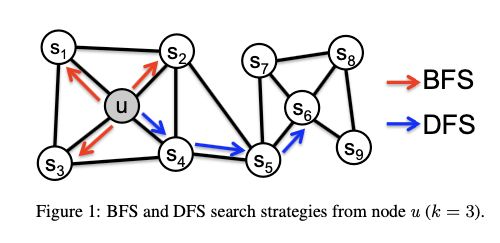
Node2Vec模型的几个步骤：
1、预处理计算出节点之间的转移概率（即从节点$u$到节点$v$的概率）
假设出发节点$c_0=u$，模拟固定长度$l$的随机游走过程中，第$i$个节点$c_i$的转移概率：
$$P(c_i=x|c_{i-1}=v)=\{\begin{array}{l}\frac{{\pi }_{vx}}{Z}if(v,x)\in E\\ 0otherwise\end{array}$$

${\pi }_{vx}$为节点$v$与$x$之间的未归一化转移概率，$Z$为归一化常数。
评估随机游走的转移未归一化概率${\pi }_{vx}$（从顶点$v$游走到下一个顶点$x$的概率），定义${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot w_{vx}$，其中${\alpha }_{pq}(t,x)$为边$(t,x)$偏置项，$w_{vx}$为边的权重，若没有权重则$w_{vx}=1$，${\alpha }_{pq}(t,x)$表达式：
$${\alpha }_{pq}(t,x)=\{\begin{array}{l}\frac{1}{p}{d}_{tx}=0\\ 1d_{tx}=1\\ \frac{1}{q}{d}_{tx}=2\end{array}$$

根据以上公式我们可以计算出${\pi }_{vx}$从而得到转移概率$P(c_i=x|c_{i-1}=v)$。

这里涉及到两个参数$p$和$q$：

• 参数$p$是控制下一步是否需要重新访问上一个节点，如果$p$值设置的很大（大于$max(q,1)$），则将基本上不会访问$t$顶点。相反，若$p$值设置的很小（小于$min(q,1)$），则很大可能重新访问$t$顶点。所以一般情况下，$p$值会设置的比较大。
• 参数$q$是控制下一步游走的方向，是靠近$t$的顶点还是远离$t$的顶点。如果$q$设置为1，则下一步将访问$X_1$，如果$q$设置为小于1，则下一步将访问$X_2$或$X_3$。也相当于控制随机游走的方式是按广度优先搜索还是深度优先搜索的方法进行。

最后Node2Vec的伪代码：

图的同构性和同质性：
同质性表示顶点之间距离很接近的顶点;
同构性表示顶点的网络结构相似的顶点;
Node2vec的缺点：对于大图来说看不到全局信息，游走有长度限制。也没有利用节点的属性信息。
模型Struc2Vec就是根据顶点的网络结构相似来对顶点进行语义表示。

19、Word2Vec：

Word2Vec包含两个算法：CBOW和Skip-gram。CBOW是通过上下文表示当前词的词向量，Skip-gram是通过当前词表示出上文的词向量。

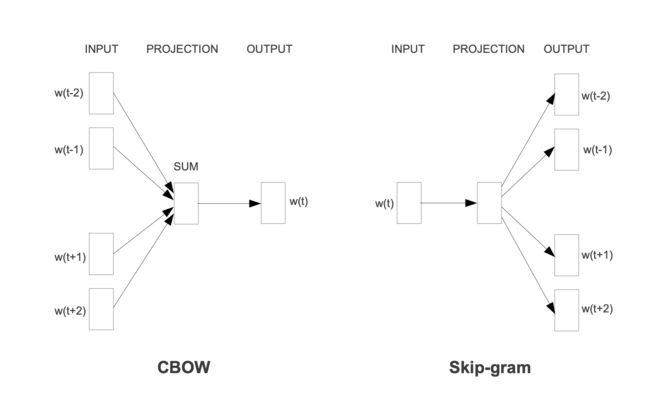
Word2Vec包含了两种实现方法：
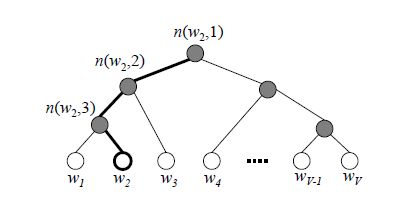
基于分层的softmax方法，通过构建Huffman树计算每个词的概率

输入层：$c_t$中包含2n个词的词向量，$v_{w_{t-n}},...,v_{w_{t-1}},v_{w_{t+1}},...,v_{w_{t+n}}\in {\mathbb{R}}^m$这里m的含义表示词向量的长度；
映射层：将输入层2n个向量求和累加取平均，即$x_w=\frac{1}{2n}{\sum }_{i=1}^{2n}{v}_{w_i}$；
输出层：输出层对应一颗二叉树，它是以语料中出现过的词当叶子节点，以各词在语料中出现的次数当权值构造出来的Huffman树，在这颗Huffman树中，叶子节点共N(=|D|)个，分别对应词典D中的词，非叶子节点N-1个。

模型训练采用二元逻辑回归的方法，往树的左子树走表示负类，往树的右子树走表示正类，然后使用sigmoid函数
$$P(+)=\sigma (x_w^T\theta )=\frac{1}{1+e^{-x_w^T\theta }}$$

然后使用梯度求解最大似然的方法训练模型。

Huffman树对于处理高频词具有很大的优势，但是对于低频词则需要很大的开销。
负采样方法，假设一个词序列$(w_{t-n},...,w_{t-1},w_t,w_{t+1},...,w_{t+n})$,$w_t$与前后2n个词具有相关性，作为正样本，然后从其他词中采样和$w_t$组合成负样本，然后同样使用二元逻辑回归的方法训练模型。
采样方法采用全局采样，词频作为采样概率：
$$p(w)=\frac{count(w{)}^{\frac{3}{4}}}{{\sum }_{u\in vocab}count(u{)}^{\frac{3}{4}}}$$

20、RNN：

RNN语言模型，如下图是一个双向循环网络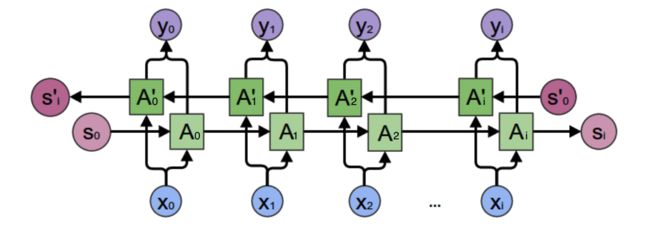
网络的输入有两个：上一个时刻的记忆状态和当前时刻的输入；输出：当前时刻的输出
$$\{\begin{array}{l}{s}_t=f(U{x}_t+W{s}_{t-1})\\ o_t=g(V{s}_t)\end{array}$$

RNN虽然可以处理序列数据集，但是对于长序列容易出现梯度消失的问题。为什么会出现这个问题？是因为模型的输入带有上一时刻的状态，在进行训练时反向传播梯度是一个累乘的过程，使用tanh或sigmoid作为激活函数，随着序列的不断加长，梯度会逐渐消失。
解决梯度消失的方法：选择更合适的激活函数，如ReLU；使用其他网络，如LSTM。
RNN很难做并行计算，因为在计算t时刻的数据时必须确保t-1时刻的数据已经计算好。

20、LSTM：

LSTM在RNN的基础上加入门控机制：输入门、遗忘门和输出门。
以下的$\circ$操作符为按元素乘法
输入门：$i_t=\sigma (W_i\cdot [h_{t-1},x_t]+b_i)$
遗忘门：$f_t=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$
候选状态：${\tilde{c}}_t=\tanh (W_c\cdot [h_{t-1},x_t]+b_c)$
当前状态：$c_t=f_t\circ c_{t-1}+i_t\circ {\tilde{c}}_t$，从当前状态的计算可以看出遗忘门是控制上一时刻的状态是否要被遗忘，输入门控制当前的候选状态是否要参与计算。
输出门：$o_t=\sigma (W_o\cdot [h_{t-1},x_t]+b_o)$
单元输出：$h_t=o_t\circ \tanh (c_t)$，输出门控制当前状态的输出。

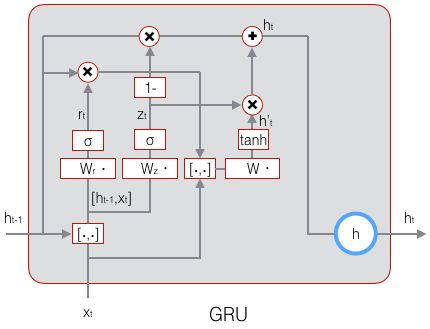
GRU是在LSTM的基础上做了一些简化，将三个门变成两个门：更新门和重置门。
更新门：$z_t=\sigma (W_z\cdot [h_{t-1},x_t]+b_z)$
重置门：$r_t=\sigma (W_r\cdot [h_{t-1},x_t]+b_r)$
候选输出：${\tilde{h}}_t=\tanh (W\cdot [r_t\circ h_{t-1},x_t]+b)$
单元输出：$h=(1-z_t)\circ h_{t-1}+z_t\circ {\tilde{h}}_t$

面试可能会涉及到的问题：
RNN、LSTM和GRU的联系和区别？
联系是三个模型都是处理序列数据的语言模型，都有记忆状态的能力；区别是RNN对短时记忆较强，LSTM和GRU是门控机制决定对前序状态的记忆，RNN对长序列的训练容易出现梯度爆炸或梯度消失的问题。LSTM和GRU是对RNN处理长序列问题的一种优化。

21、Transformer：

Transformer是一个基于自注意力机制的序列模型，主要包含两个部分：编码器和解码器，如下图所示：

Encoder：包含多头注意力层和MLP层，两个模块都加了残差连接。编码器的输入是input embedding+positional encoding。
Decoder：解码器比编码器多了一个带masked的多头注意力层，即一个带masked的多头注意力层、多头注意力层和MLP层，解码器的输入分两个，一个是output embedding+positional encoding，这个是输入到带masked的多头注意力层，另一个是将编码器的输出（K和V）+带masked的多头注意力层的输出（Q），输入到下一层的多头注意力层。因此这里的多头注意力不是自注意力。

Transformer中的Encoder和Decoder可以进行叠加，如图中的$N\times$

自注意力层：$Attention(Q,K,V)=softmax(\frac{Q{K}^t}{\sqrt{d_k}})V$，其主要作用就是看Q和K的相似度，如果Q和K的相似度很高，作用在V的权重就越大，否则作用在V的权重就越小。比较常用的注意力机制有两种：加法注意力机制和点乘注意力机制，加法注意力机制可以处理不等长的K和Q的情况。

带masked的自注意力层：这个只是比自注意力层多加了一个masked标记，因为在做解码的时候，计算t时刻只能用t-1及之前的数据，所以要对t时刻的数据做标记，这个标记是在进入softmax之前做，将t及之后的数据设置成一个很大的负数，这样进入softmax之后它们得到的权重就都为0。

Transformer中的注意力层是多头注意力，思路是将K、Q、V投影到低维，投影h次，然后再做h次的自注意力计算，再把每次计算结果并在一起，最后投影回来得到最终的结果。为什么要这么做？因为在注意力层就是做内积计算，没有参数的学习，做多头注意力是想通过多次投影学习到K、Q、V中的不同信息，再做注意力计算。

Transformer中的注意力层除了一个$\sqrt{d_k}$，对于这个操作，如果$d_k$的值不大时，除不除没什么关系；如果$d_k$的值比较大（即两个向量的长度比较长）时，K和Q计算出来的相似度可能比较大，这样softmax出来的权重可能会更加靠近1，剩下的值更加靠近0，导致得到的结果分布在softmax的两端，使得梯度较小，模型训练不下去。

Transformer和RNN记录序列信息区别：Transformer是通过Attention在全局数据的情况下计算，输出带有序列信息的语义表示。RNN则是通过将上一时刻的输出加入到当前时刻的输入，来计算得到带有序列信息的语义表示。

Transformer中的Postional encoding：主要是因为attention计算并没有关注序列数据的位置信息，在attention计算的过程中，打乱序列数据的顺序输出的结果是一致的，所以需要额外加入序列的位置信息，让attention计算带有序列数据的位置信息。

Transformer中的残差连接作用：一是残差可以解决梯度消失的问题；二是残差可以解决权重矩阵退化的问题（即随着的网络层数的增加，输入的特征数据区分度越来越小，权重得不到更新）。

ELMO、GPT、BERT都是预训练模型，可以比较好的处理多语义问题，它们通过预训练得到一个模型，在使用时，模型微调，根据输入数据的上下文输出对应的向量表示。不同于之前的Word2Vec，模型输出就是一一对应的词向量。

22、BERT:

BERT是基于Transformer的编码器实现的一个双向语言模型，BERT包含两步：pre-training和fine-tunin，如下图：

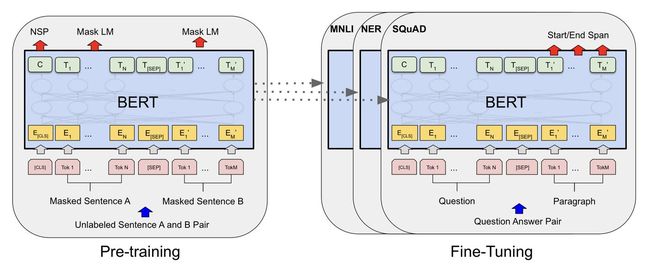
预训练模型是使用没有标签的数据训练，得到一个初始的模型，微调是针对每个下有任务，构建一个和预训练模型一样的网络，然后在预训练好的模型参数之上输入带标签的数据继续训练，调整模型权重。
输入：可以是一个句子，也可以是一个句子对，但是不管是句子还是句子对，都是将其构造成一个序列输入到BERT模型中，BERT的embedding输入一共有三个：Token embedding（词的embedding），segment embedding（词在哪个句子的embedding）以及position embedding（词在整个序列中的embedding）：
BERT输入的词元会做掩码操作，输入序列中有15%的词元会随机替换成掩码，由于在下游任务中没有掩码操作，造成前后训练不一致，所以这15%的替换成掩码的词元中只有80%真正替换，10%的词元随机替换成其他词，10%的词元什么都不做，就放在那里用它做预测。

BERT和ELMo以及GPT的区别和联系：GPT使用的是Transformer中的解码器，只考虑了从左到右单向的过程，用左边的上下文信息预测未来。ELMo是基于双向的LSTM实现的，而BERT是基于Transformer的编码器实现的一个双向网络。三者都是预训练模型，预训练模型的下游任务有两种方式：ELMo是基于特征，对于每个下游任务，构造一个相关的模型，将预训练模型的输出作为一个新特征和数据一起输入到模型中。GPT和BERT都是基于微调的，每个下游任务对模型进行一些微调，然后输入数据将预训练好的模型再训练。语言模型是单向的，通过前面的词预测未来，但是对于一些任务，如问答、句子的情感分析，是需要知道整个问题或知道整个句子才能做出比较好的回答或情感判断。BERT做nlp上的分类任务更有优势，GPT做nlp上的生成类任务更有优势。
WordPiece embedding：将词切成词根的形式，在大规模数据中保留词根可以相对缩小词典大小。同时可以较好的处理OOV(Out of Vocabulary)、低频词/稀疏词以及单词不同形态的问题。

Transformer、BERT面试相关问题：
1、Transformer为什么使用dot-product attention？
因为dot-product对Transformer来说更是容易实现，效果也不比加法attention差。并且相比矩阵运算，dot-product比additive计算更加快速。

23、优化器：

模型优化使用梯度下降算法更新参数：${\theta }_{t+1}={\theta }_t-\alpha \nabla L({\theta }_t)$其中$\nabla L({\theta }_t)$表示梯度。
1、GD（梯度下降）：每次更新参数时需要遍历所有的样本，缺点是①当训练样本很大时，训练非常耗时；②由于每次更新参数都是朝当前的最优方向，很容易会陷入局部最优。
2、SGD（随机梯度下降）：每次训练一个样本就更新一次参数：${\theta }_{t+1}={\theta }_t-\alpha \nabla L(\theta ;x_i,y_i)$。因此，SGD加速了模型的训练，同时能都适用online learning。但是由于每一个样本就是更新参数，导致随机梯度的方差很大，模型训练迭代不稳定，一般采用小批量梯度下降法（Mini-Batch Gradient Descent）：${\theta }_{t+1}={\theta }_t-\alpha \frac{1}{m}\sum _{j=1}^m\nabla L(\theta ;x_{i_j},y_{i_j})$。为了避免数据集特定顺序可能给模型训练带来影响，通常都会对数据集的shuffle一下。缺点：由于小批量样本更新，可能会引入样本噪声，权重更新不稳定。对学习率要求比较高，过大容易震荡，过小收敛很慢。
3、SGDM（加入动量机制的随机梯度下降）：当前动量由上一次迭代动量和当前梯度决定：$v^t=\lambda v^{t-1}-\eta \nabla L({\theta }^t)$，梯度更新：${\theta }_t={\theta }_{t-1}+v_t$。其中$\lambda$是动量的衰减权重。加入动量之后，可以保留一定的更新趋势，可以解决卡在局部最优点的问题。
4、Adagrad：使用迭代次数和累积梯度对学习率进行自动衰减：${\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{{\sum }_{i=0}^{t-1}(g_i{)}^2}}{g}_{t-1}$。使得模型可以在最初较大的学习率下快速收敛，后面在小的学习率下精调模型。缺点：迭代后最后，学习率非常小时，模型很难真正收敛。
5、RMSProp（Root Mean Square Prop）：加入迭代衰减的自适应梯度下降，${\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{v_t}}{g}_{t-1}，v_1=g_0^2，v_t=\alpha v_{t-1}+(1-\alpha )(g_{t-1}{)}^2$。梯度迭代时，使得最近的梯度作用很大，这样解决了梯度累积过大，导致学习率衰减很小参数得不到更新的问题。
6、Adam：差不多是SGDM和RMSProp的结合，即加入了动量和学习率衰减，${\theta }_t={\theta }_{t-1}+\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t$，其中${\hat{m}}_t$使用SGDM的方式计算：$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_{t-1}，{\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}$。${\hat{v}}_t$使用RMSProp的计算方法：$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)(g_{t-1}{)}^2，{\hat{v}}^t=\frac{v_t}{1-{\beta }_2^t}$。该方法基本上解决上述优化器遇到的所有问题，因此用的很多，尤其是NLP领域。

24、Softmax上溢、下溢。

上溢和下溢是舍入误差造成的，上溢：大量级的数被近似为$\infty$或$-\infty$。下溢：接近零数近似为0。

25、Layer-Norm和Batch-Norm

Layer-Norm：模型训练输入的三维数据$batch\times features\times d$($d$表示每个特征的向量维度)，Layer-Norm对每个样本做normalize。
Batch-Norm：模型训练输入的三维数据$batch\times features\times d$($d$表示每个特征的向量维度)，Batch-Norm对每个batch中的每个特征做normalize。

从两个归一化处理的方式看，Batch—Norm对每个Batch中的所有样本做每个特征的normalize，做预测时需要记录全局的$\mu$和$Var$，这将导致如果样本变化很大时，Batch—Norm也会有较大的波动，从而降低模型的泛化性。尤其是对于序列数据，可能样本间的序列长度差异会比较大。而对于Layer-Norm则不会出现这个问题，因为它是对样本做normalize。也不需要记录$\mu$和$Var$。