(数字图像处理MATLAB+Python)第五章图像增强-第六节:其他图像增强技术
文章目录
- 一:基于对数图像处理模型的图像增强
-
- (1)对数图像处理模型(LIP)
- (2)基于对数图像处理模型的增强
- 二:图像去雾增强
-
- (1)图像去雾模型
- (2)基于暗原色先验的去雾方法
- (3)基于暗原色先验的低照度图像增强
一:基于对数图像处理模型的图像增强
基于对数图像处理模型的图像增强:是一种图像处理技术,旨在改善图像的质量和可视性。该方法基于对数变换,通过将图像转换为对数域,并对其进行处理来增强图像的对比度和亮度。在对数图像处理模型中,图像被看作是在一个对数域中的值的分布。通过对数变换,原始图像中的低灰度值被压缩到较小的范围内,而高灰度值则被拉伸到更广的范围内。这样可以增强图像的对比度和细节,并使暗部细节更加明显
(1)对数图像处理模型(LIP)
对数图像处理模型:基本原理是将原始图像的像素值通过对数变换映射到对数域,然后在对数域中对图像进行处理,最后再将处理后的图像通过指数变换映射回原始像素值
设原始图像为 f ( x , y ) f(x,y) f(x,y),对数变换为 g ( x , y ) = l o g ( 1 + f ( x , y ) ) g(x,y)=log(1+f(x,y)) g(x,y)=log(1+f(x,y)),指数变换为 h ( x , y ) = e x p ( g ( x , y ) ) − 1 h(x,y)=exp(g(x,y))-1 h(x,y)=exp(g(x,y))−1,则对数图像处理模型可表示为
h ( x , y ) = e x p ( l o g ( 1 + f ( x , y ) ) ) − 1 h(x,y)=exp(log(1+f(x,y)))−1 h(x,y)=exp(log(1+f(x,y)))−1
对数变换将像素值映射到对数域,并将低灰度值压缩到较小的范围内,高灰度值拉伸到更广的范围内,增强了图像的对比度和细节。处理后,指数变换将像素值从对数域映射回原始像素值,得到处理后的图像
LIP基础向量运算
- 对数加法运算: f 1 ( x , y ) ⊕ f 2 ( x , y ) = f 1 ( x , y ) + f 2 ( x , y ) − f 1 ( x , y ) ⋅ f 2 ( x , y ) M f_{1}(x, y) \oplus f_{2}(x, y)=f_{1}(x, y)+f_{2}(x, y)-\frac{f_{1}(x, y) \cdot f_{2}(x, y)}{M} f1(x,y)⊕f2(x,y)=f1(x,y)+f2(x,y)−Mf1(x,y)⋅f2(x,y)
- 对数乘法运算: λ ⊗ f 1 ( x , y ) = M − M ( 1 − f 1 ( x , y ) M ) λ \lambda \otimes f_{1}(x, y)=M-M\left(1-\frac{f_{1}(x, y)}{M}\right)^{\lambda} λ⊗f1(x,y)=M−M(1−Mf1(x,y))λ
- 对数减法运算: f 1 ( x , y ) Θ f 2 ( x , y ) = M ⋅ f 1 ( x , y ) − f 2 ( x , y ) M − f 2 ( x , y ) f_{1}(x, y) \Theta f_{2}(x, y)=M \cdot \frac{f_{1}(x, y)-f_{2}(x, y)}{M-f_{2}(x, y)} f1(x,y)Θf2(x,y)=M⋅M−f2(x,y)f1(x,y)−f2(x,y)
LIP基本同态函数:
- 正变换: φ ( f ) = − M ⋅ ln ( 1 − f ( x , y ) M ) \varphi(f)=-M \cdot \ln \left(1-\frac{f(x, y)}{M}\right) φ(f)=−M⋅ln(1−Mf(x,y))
- 反变换: φ − 1 ( f ) = M ⋅ ( 1 − e ( − f ( x , y ) M ) ) \varphi^{-1}(f)=M \cdot\left(1-e^{\left(\frac{-f(x, y)}{M}\right)}\right) φ−1(f)=M⋅(1−e(M−f(x,y)))
(2)基于对数图像处理模型的增强
**基于对数图像处理模型的增强:如下
- f ( x , y ) f(x,y) f(x,y)是原图的灰度色调函数
- f ′ ( x , y ) f^{\prime}(x,y) f′(x,y)是增强后图像的灰度色调函数
- A ( x , y ) A(x,y) A(x,y)为 n × n n×n n×n邻域的灰度色调函数的平均值
- α \alpha α用于调整对比度
- β \beta β用于调整锐化效果
f ′ ( x , y ) = α ⊗ A ( x , y ) ⊕ β [ f ( x , y ) Θ A ( x , y ) ] f^{\prime}(x, y)=\alpha \otimes A(x, y) \oplus \beta[f(x, y) \Theta A(x, y)] f′(x,y)=α⊗A(x,y)⊕β[f(x,y)ΘA(x,y)]
将 f ( x , y ) f(x,y) f(x,y)进行基本正态函数的正变换,且令
f ˉ ( x , y ) = 1 − f ( x , y ) M \bar{f}(x,y)=1-\frac{f(x,y)}{M} fˉ(x,y)=1−Mf(x,y)
化简后公式如下
ln f ˉ ′ ( x , y ) = α ⋅ ln A ˉ ( x , y ) + β ⋅ [ ln f ˉ ( x , y ) − ln A ˉ ( x , y ) ] ln A ˉ ( x , y ) = 1 n × n ∑ k = x − n 2 x + n 2 ∑ l = y − n 2 y + n 2 ln f ˉ ( x , y ) \begin{array}{c}\ln \bar{f}^{\prime}(x, y)=\alpha \cdot \ln \bar{A}(x, y)+\beta \cdot[\ln \bar{f}(x, y)-\ln \bar{A}(x, y)] \\\ln \bar{A}(x, y)=\frac{1}{n \times n} \sum_{k=x-\frac{n}{2}}^{x+\frac{n}{2}} \sum_{l=y-\frac{n}{2}}^{y+\frac{n}{2}} \ln \bar{f}(x, y)\end{array} lnfˉ′(x,y)=α⋅lnAˉ(x,y)+β⋅[lnfˉ(x,y)−lnAˉ(x,y)]lnAˉ(x,y)=n×n1∑k=x−2nx+2n∑l=y−2ny+2nlnfˉ(x,y)
算法步骤如下
- 求灰度色调函数
- 进行基本正态函数的正变换
- 求以点 ( x , y ) (x,y) (x,y) 中心的 n × n n×n n×n邻域的平均值
- 进行基于对数图像处理模型的增强处理
- 进行基本正态函数的反变换
二:图像去雾增强
图像去雾增强:图像去雾增强是指在图像中去除因雾霾、烟雾等自然因素导致的视觉模糊和降低图像对比度的现象,以提高图像的质量和可视性的过程。图像去雾增强的方法主要包括以下几种
- 基于物理模型的方法:该方法基于天空、雾、场景等的物理模型,对图像进行建模,然后利用图像恢复技术推导出清晰图像。该方法具有较高的精度和可靠性,但需要大量的先验知识和计算资源
- 基于暗通道先验的方法:该方法利用图像中低光强区域的信息,估计出图像中的全局大气光强度和雾的浓度,然后根据这些参数对图像进行去雾。该方法计算简单,且能够取得良好的去雾效果,但对于图像中存在颜色较为单一区域时,可能会出现伪影现象
- 基于深度学习的方法:该方法利用深度学习网络,通过训练来学习图像中的特征和去雾模式,然后对图像进行去雾。该方法需要大量的训练数据,但具有较好的泛化能力和实时性
- 基于统计方法的方法:该方法通过分析图像中的像素分布和灰度分布,对图像进行去雾增强。该方法不需要先验知识,计算简单,但对于复杂的场景和光照条件,效果可能不理想
图像去雾增强在自然图像处理、计算机视觉和遥感图像处理等领域具有广泛应用,例如无人机视觉、车载视觉等
(1)图像去雾模型
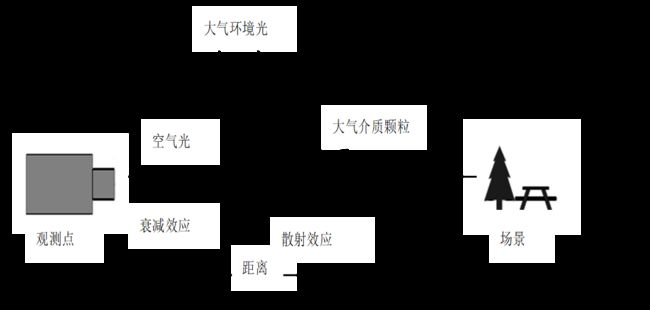
图像去雾模型:图像去雾模型基于物理模型,主要描述了雾霾天气下的图像成像过程,其数学表达式为
- I ( x ) I(x) I(x)表示观测到的图像
- J ( x ) J(x) J(x)表示场景反射率
- t ( x ) t(x) t(x)表示雾的浓度
- A A A表示全局大气光强度
I ( x ) = J ( x ) t ( x ) + A ( 1 − t ( x ) ) I(x)=J(x)t(x)+A(1-t(x)) I(x)=J(x)t(x)+A(1−t(x))
在这个模型中,假设场景的反射率 J ( x ) J(x) J(x) 和雾的浓度 t ( x ) t(x) t(x) 是空间不变的,即不同的位置处的雾的浓度相同,这个假设在实际应用中通常是成立的。因此,我们可以将 J ( x ) J(x) J(x) 和 t ( x ) t(x) t(x) 看作常数。这个模型可以被理解为在场景反射率和雾的浓度的影响下,观测到的图像 I ( x ) I(x) I(x) 是由原始场景反射率 J ( x ) J(x) J(x) 经过一个衰减因子 t ( x ) t(x) t(x),再加上一部分来自大气光的贡献 ( 1 − t ( x ) ) A (1-t(x))A (1−t(x))A 所组成
根据这个模型,我们可以通过估计大气光 A A A 和雾的浓度 t ( x ) t(x) t(x),以及对场景反射率 J ( x ) J(x) J(x) 的恢复,来实现对图像的去雾增强。在实际应用中,通常采用基于暗通道先验的方法来估计大气光和雾的浓度,然后通过先验约束和优化算法来对场景反射率进行恢复
(2)基于暗原色先验的去雾方法
基于暗原色先验的去雾方法:是一种计算机视觉中用于提高图像质量的技术。该方法的目标是从雾化图像中还原出原始场景的信息。设 I ( x , y ) I(x,y) I(x,y) 为输入的雾化图像在坐标 ( x , y ) (x,y) (x,y) 处的像素值, J ( x , y ) J(x,y) J(x,y) 为去雾后在坐标 ( x , y ) (x,y) (x,y) 处的像素值。假设场景中的真实颜色为 C ( x , y ) C(x,y) C(x,y),雾的遮挡因子为 t ( x , y ) t(x,y) t(x,y),则有以下的传输模型
-
A ( x , y ) A(x,y) A(x,y)表示大气光照
-
假设在整个图像中 A ( x , y ) A(x,y) A(x,y) 是常量,不失一般性的假设 A ( x , y ) = A A(x,y) = A A(x,y)=A
I ( x , y ) = t ( x , y ) C ( x , y ) + ( 1 − t ( x , y ) ) A ( x , y ) I(x,y)=t(x,y)C(x,y)+(1 - t(x,y))A(x,y) I(x,y)=t(x,y)C(x,y)+(1−t(x,y))A(x,y)
我们假设场景的颜色是具有暗原色先验的,即颜色的 RGB 通道中的最小值是一个固定的常数 α \alpha α,即 -
C r ( x , y ) C_r(x,y) Cr(x,y)、 C g ( x , y ) C_g(x,y) Cg(x,y) 和 C b ( x , y ) C_b(x,y) Cb(x,y) 分别表示 C ( x , y ) C(x,y) C(x,y) 的红、绿、蓝三个通道的值
min { C r ( x , y ) , C g ( x , y ) , C b ( x , y ) } ≥ α \min \left\{C_{r}(x, y), C_{g}(x, y), C_{b}(x, y)\right\} \geq \alpha min{Cr(x,y),Cg(x,y),Cb(x,y)}≥α
基于暗原色先验,我们可以得到一个估计场景颜色 C ′ ( x , y ) C'(x,y) C′(x,y) 的下界 C ~ ( x , y ) \tilde{C}(x,y) C~(x,y):
- ω ( x , y ) \omega(x,y) ω(x,y) 是一个权重值,定义为: ω ( x , y ) = exp { − β min { I r ( x , y ) , I g ( x , y ) , I b ( x , y ) } } \omega(x, y)=\exp \left\{-\beta \min \left\{I_{r}(x, y), I_{g}(x, y), I_{b}(x, y)\right\}\right\} ω(x,y)=exp{−βmin{Ir(x,y),Ig(x,y),Ib(x,y)}}
- β \beta β 是一个正的系数
C ~ ( x , y ) = 1 1 − ω ( x , y ) ( I ( x , y ) − ( 1 − ω ( x , y ) ) A ) \tilde{C}(x, y)=\frac{1}{1-\omega(x, y)}(I(x, y)-(1-\omega(x, y)) A) C~(x,y)=1−ω(x,y)1(I(x,y)−(1−ω(x,y))A)
最终的估计颜色值 C ′ ( x , y ) C'(x,y) C′(x,y) 取决于 C ~ ( x , y ) \tilde{C}(x,y) C~(x,y) 和 α \alpha α 之间的最大值,即
C ′ ( x , y ) = max { C ~ ( x , y ) , α } C^{\prime}(x, y)=\max \{\tilde{C}(x, y), \alpha\} C′(x,y)=max{C~(x,y),α}
这样,我们就可以得到去雾后的图像 J ( x , y ) J(x,y) J(x,y)
J ( x , y ) = t ( x , y ) C ′ ( x , y ) + ( 1 − t ( x , y ) ) A J(x, y)=t(x, y) C^{\prime}(x, y)+(1-t(x, y)) A J(x,y)=t(x,y)C′(x,y)+(1−t(x,y))A
(3)基于暗原色先验的低照度图像增强
基于暗原色先验的低照度图像增强:将低照度图像反转后,其图像表征及直方图表征与雾天图像具有很高的相似性,算法步骤如下
- 求得输入低照度图像的反转图像: R c ( x ) = 255 − I c ( x ) R^{c}(x)=255-I^{c}(x) Rc(x)=255−Ic(x)
- 进行暗原色先验去雾,获得无“雾”图像
- 反转无“雾”图像 ,获得低照度增强图像

