字典树(Trie/前缀树)详解
目录
字典树的概念
字典树的逻辑
字典树的实现
字典树小结
例题强化
字典树的概念
字典树(Trie)是一种空间换时间的数据结构,是一棵关于“字典”的树,主要用于统计、排序和保存大量的字符串。字典树是通过利用字符串的公共前缀来节约存储空间,因此字典树又叫前缀树。字典树是对于字典的一种存储方式。这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径,路径中每条边的字母连起来就是一个单词。
字典树的逻辑
在学习字典树之前我们先来看这样一个问题:
给你n个单词,并进行x次查找,每次查找随机一个单词word。
问:word是否出现在这n个单词中?
想想看,这像不像平常我们查字典?比如要在字典中查找单词“abandon”,我们一般是找到首字母为'a'的部分,然后再找第二个单词为‘b’的部分······如果字典中存在这个单词,那么我们最后就可以找到这个单词,反之则不能。
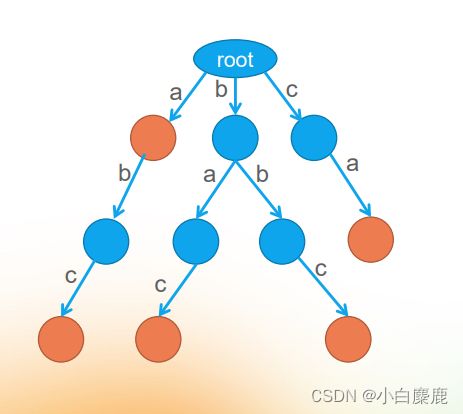
接下来,我们通过图解存储了单词{“a”,"abc",“bac”,“bbc”,"ca" }的字典树对上方内容进行解释:
从这张图我们可以看出,这棵字典树的每条边上都有一个字母(可以类比查字典时查找的第k个字母来理解),并且这棵树的一些节点被指定成了标记节点,用于表示到此为止是一个完整的单词。
字典树的实现
通过上面的图不难发现,字典树并不是二叉树,所以字典树的结构定义和二叉树的并不同,这里不要惯性思维了。通常我们定义多叉树时常用孩子表示法,像这样
struct TreeNode {
ELEMENT_TYPE value; //结点值
TreeNode* children[NUM]; //孩子结点
};字典树也类似:
struct TrieNode {
int isEnd; //该结点是否是一个串的结束
TrieNode* children[SIZE]; //字母映射表
};常规的多叉树类型一般是,一个成员存放当前节点的内容,如上方的value成员;一个成员存放所有孩子节点的地址,如上方的children[NUM]成员,其数组中存放的是一个个TreeNode*类型的孩子节点的地址。
而字典树却与其有些不同,字典树的一个成员存放的是boo/intl型的isEnd成员,用于判断当前节点是否为一个单词的结束,如果是就标记为true,这样做的目的是在查找的时候方便确定找到最后是不是一个单词,因为并不是一个单词中所有的子串都是一个单词,例如”abandon“是一个单词,而其子串“ab“就不是一个单词。其另一个成员存放的也是一个指向孩子节点的指针,与常规的多叉树理解类似。
这里也许你会发现一些”端倪“:字典树的结构里好像并没有用于存储节点内容的成员,比如常规多叉树中的value成员。其实就是没有,但这并不妨碍我们实现这个功能,例如我们暂定字典中只有小写的26个字母,那么字典树的children[SIZE] 成员中SIZE就可以设置为26,那么我们就可以存储,那么我们将要查找或是存储的单词每一个字母(的ASCII值)减去一个'a' (字符a),那么其对应的值,就是我们要存放的children数组下标。了解过哈希表(散列表)的同学肯定会有一种茅塞顿开的感觉,因为这里其实就是用的哈希表的思路。下标为k的元素如果不为空(数组中的每一个元素都是一个指针)就说明这个元素有孩子节点,进而说明这个元素对应的字母是存在的。其中,一般第n层的children数组的下标k位置如果不为空,就表示这个单词中的第n个位置存在k下标位置所对应的字母。例如包含单词 "sea","sells","she" 的字典树图解如下:
在这里,我们还可以试着讨论一下为什么这个children成员用数组实现。(这一小部分内容与字典树的核心内容并没有多大关系,如果没有兴趣可以直接跳过)
相信有部分人(比如我)第一次接触字典树时对于
TrieNode* children[SIZE]这种的定义是很难认同的,因为我们可能会觉得这会浪费很多空间,为什么不用链表等其它顺序结构来实现呢?
首先,如果将数组替换为链表或其它线性结构,那么实现起来会非常繁琐,而且即使实现了,每次查找字母时都要进行一次链表的遍历,相较于数组的直接下标访问,是一个很费时的过程。
其次,这里的数组其实就是一个哈希表,哈希表的一大优点就是用空间换时间,而且一个良好的哈希表结构是必须要留有一定的空闲位置的,所以这种实现方式也并非不妥。
也许会有人想到用C++中的map/unordered_map来实现,这确实是可行的。首先,如果用map容器替换数组的话,实现起来并不是很难,理论上相较于哈希表确实会节省空间,但map的底层实现是红黑树,用一个红黑树去实现一个字典树,是不是有点小题大做了呢?其次,对于unordered_map来说,其本身就是一个哈希容器,与使用数组的本质是一样的,所以当然可行啦。
字典树小结
字典树的实现是一种哈希表和树的结合。字典树的每次插入和查找操作的时间复杂度都是O(NlogN)的,而且为了防止删除操作对树操作不可逆的损坏,所以我们一般都是在结构体中额外增加一个成员,用以表示当前节点是否被删除(专业术语叫“惰性删除”)。
例题强化
原题链接: 208. 实现 Trie (前缀树)
- 题目描述:
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
- Trie() 初始化前缀树对象。
- void insert(String word) 向前缀树中插入字符串 word 。
- boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
- boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True提示:
1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/implement-trie-prefix-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
- 参考答案:
C语言版本
typedef struct TrieNode{
int isEnd;
struct TrieNode* children[26];
} Trie;
Trie* trieCreate()
{
Trie* trie = (Trie*) calloc (1,sizeof(Trie));
return trie;
}
void trieInsert(Trie* obj, char * word)
{
int len = strlen(word);
Trie* node = obj;
for(int i = 0; i < len; i++)
{
if(node->children[word[i] - 'a'] == NULL)
node->children[word[i] - 'a'] = (Trie*) calloc (1,sizeof(Trie));
node = node->children[word[i] - 'a'];
}
node->isEnd = true;
}
bool trieSearch(Trie* obj, char * word)
{
int len = strlen(word);
Trie* node = obj;
for(int i = 0; i < len; i++)
{
if(node->children[word[i] - 'a'] == NULL)
return false;
node = node->children[word[i] - 'a'];
}
return node->isEnd;
}
bool trieStartsWith(Trie* obj, char * prefix)
{
int len = strlen(prefix);
Trie* node = obj;
for(int i = 0; i < len; i++)
{
if(node->children[prefix[i] - 'a'] == NULL)
return 0;
node = node->children[prefix[i] - 'a'];
}
return true;
}
void trieFree(Trie* obj)
{
for(int i = 0; i < 26; i++)
{
if(obj->children[i] != NULL)
trieFree(obj->children[i]);
}
free(obj);
}
/**
* Your Trie struct will be instantiated and called as such:
* Trie* obj = trieCreate();
* trieInsert(obj, word);
* bool param_2 = trieSearch(obj, word);
* bool param_3 = trieStartsWith(obj, prefix);
* trieFree(obj);
*/C++版本
class Trie {
private:
bool isEnd;
vector children;
public:
Trie() : isEnd(false) , children(26) {}
//插入操作
void insert(string word)
{
Trie* node = this;
for(char ch : word)
{
if(node->children[ch - 'a'] == nullptr)
{
node->children[ch - 'a'] = new Trie();
}
//相对于node = node->next;
node = node->children[ch - 'a'];
}
node->isEnd = true;
}
//查找单词
bool search(string word)
{
Trie* node = this;
for(char ch : word)
{
if(node->children[ch - 'a'] == nullptr)
return false;
node = node->children[ch - 'a'];
}
return node->isEnd;
}
//查找前缀
bool startsWith(string prefix)
{
Trie* node = this;
for(char ch : prefix)
{
if(node->children[ch - 'a'] == nullptr)
return false;
node = node->children[ch - 'a'];
}
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/