嵌入式硬件：放大器电路仿真

说明

书上的放大电路图很多都是理论图，和实际应用有所差异。比如下面这个同向放大电路：

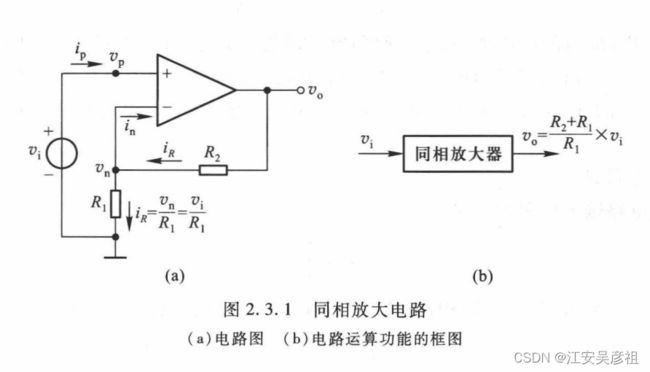
理论分析没有问题，但是我们实际应用的图应该是下面这样：

需要多增加一个续流电阻。如果没有续流电阻，则放大器正向端的电容没有电流输入，无法工作。因此，本文基于proteus仿真，做了此文来记录实际应用中的放大电路。其中示波器各通道命名为OS1、OS2等，本文电路中出现OS1等就表示接到了示波器的通道1。

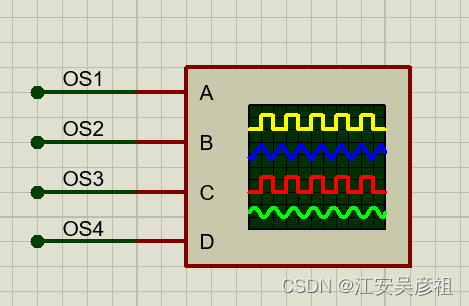
同向放大电路

理论图如下：

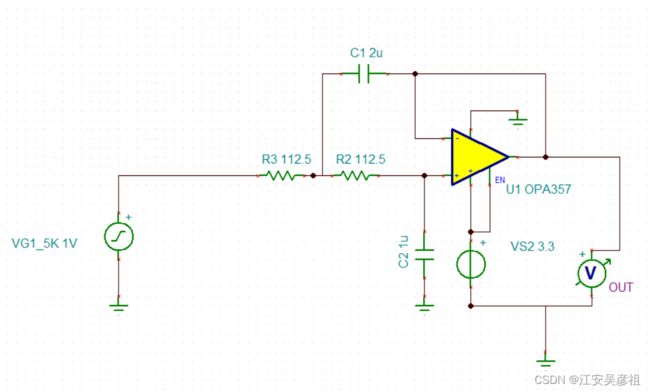
实际图如下：

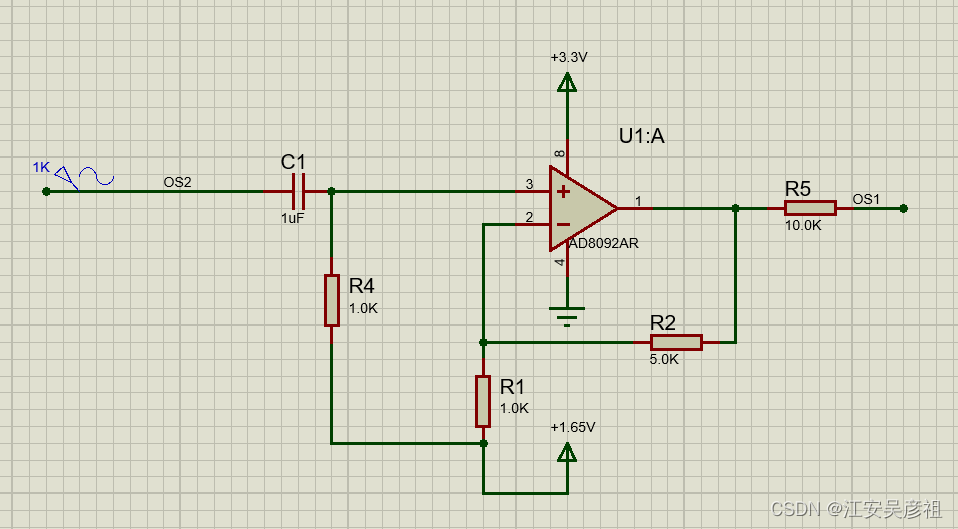
其中电容C1为耦合输入电容，如果其值比较小，根据电容阻抗公式：

电容容值越小，其容抗越大，则只有更高频率的信号才可以通过。
而如果电容值选择过大，则低频噪声信号也可以通过。

反向放大电路

如下：

实际电路图如下：

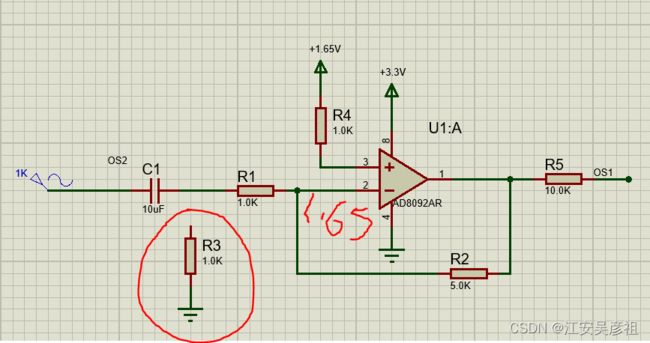
注意：此时不能加续流电阻R3，电容C1充电是通过R1进行充电的
效果如下：

放大器滤波电路

放大器的一个重要应用就是滤波效果，我们假设有以下三个正弦信号混叠在一起，如下图：

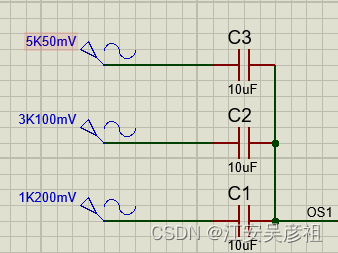
其中5K50mV意思是频率是5KHZ，振幅是50mV。则其在示波器中形状如下：

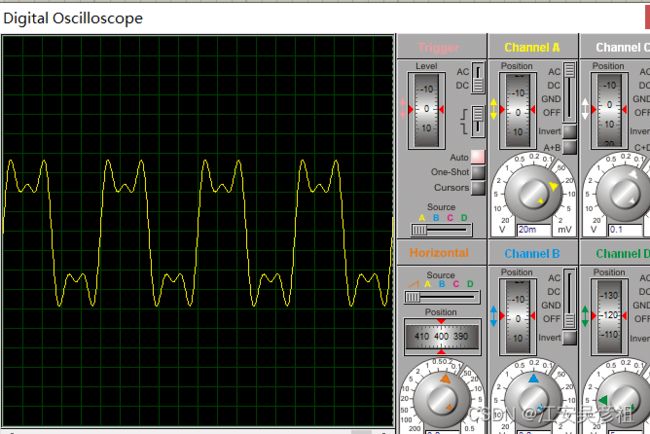
我们下面选择各种滤波电路来将信号还原出来。

低通滤波电路

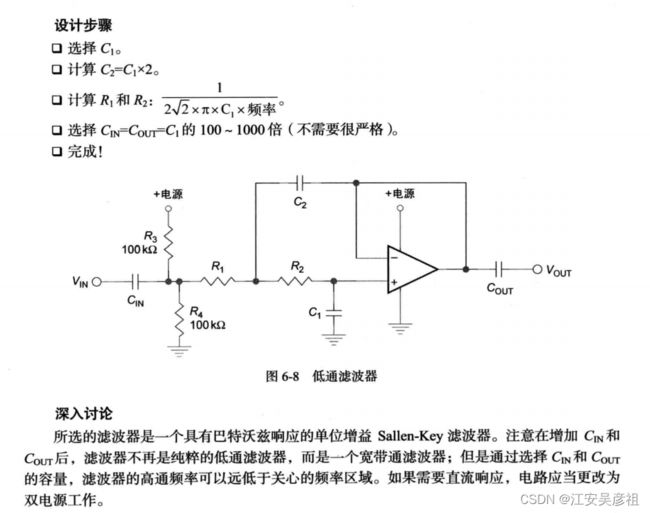
实际电路图如下：
我们选择滤波器的截止频率为1khz，则：
$R_1\times C_1=\frac{1}{2\sqrt{2}\times \pi \times f}$
代入f=1000HZ，则：
$R_1\times C_1=\frac{1}{8.8857\times f}=\frac{1}{8885.7}=1.125\times 10^{-4}$

选择 R1=R2=100 $\Omega$
则 C1=$1.125\times 10^{-6}F=1.125uF$
由于电容容值一般不连续且精度没有电阻高，而电阻可选，因此互换：
R1=R2=112.5 $\Omega$
则 C1=$1\times 10^{-6}F=1uF$
则 C2=$2\times 10^{-6}F=2uF$

proteus仿真

此时proteus仿真效果如下：

其中黄色是输入的信号，包括1K、3K、5K的正弦波。蓝色是滤出来的信号，我们发现其频率为1us。因此该滤波电路设计正确。

除此之外，还可以使用更专业的模电仿真软件：这里选择TINA TI，软件才100M大小，可以很方便的分析出电路响应。

TINA TI仿真

如下图所示的是一个500KHZ的低通滤波器，来源为OPA357的数据手册：

我们分析其电路响应为：

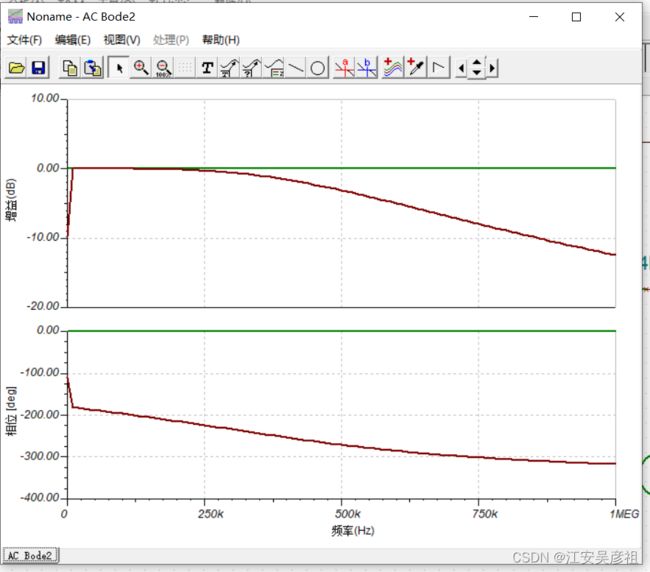
输入信号为50KHZ的方波，则输入输出信号为：

可以发现该软件特别方便设计滤波器。

我们设计我们上面在proteus的电路，分析其电路响应：

分析结果如下：

可以看到对于5KHZ的信号，其滤波效果是比较好的。

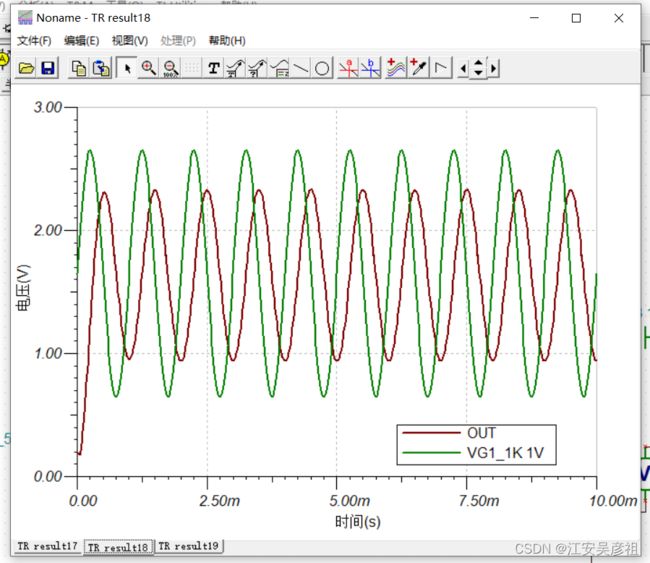
对于1KHZ的信号，其稍微有所衰减。

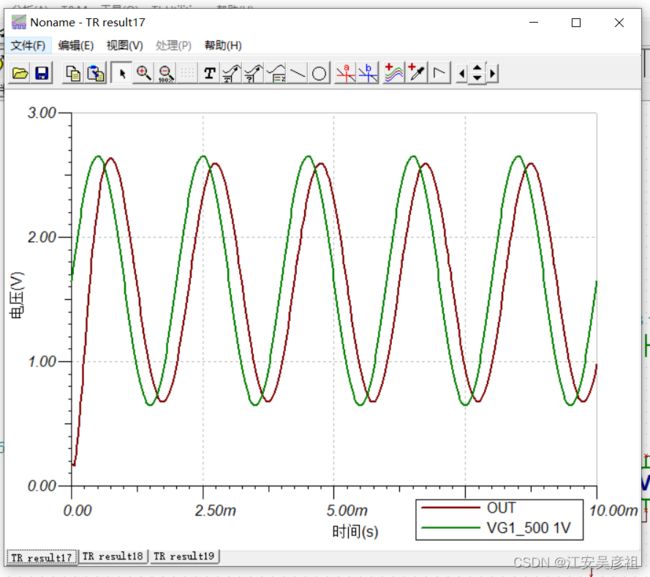
对于500HZ的信号，基本上没有衰减。
分析其频域特性：可以发现其较好的低通滤波特性。

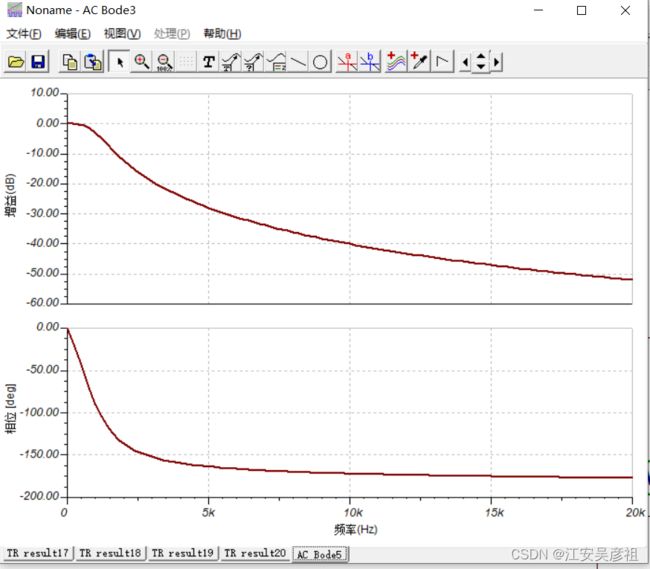
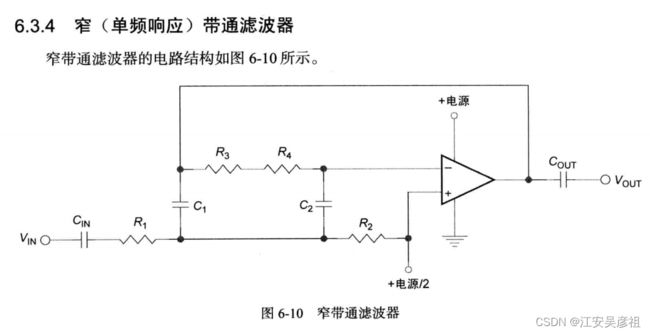
窄带滤波电路

preteus仿真

同样的，我们设计一个3KHZ的窄带滤波电路，将1K、3K、5K等信号中的3K滤除出来。

我们选择滤波器的通带频率为3khz，则：
$R_1\times C_1=\frac{1}{2\times \pi \times f}$

代入f=3000HZ，则：

$R_1\times C_1=\frac{1}{6.28318\times f}=\frac{1}{18849.54}=5.305\times 10^{-5}$

选择 R1=R2=100 $\Omega$
则 C1=$5.305\times 10^{-7}F=0.5305uF$
由于电容容值一般不连续且精度没有电阻高，而电阻可选，因此互换：
R1=R4=530.5 $\Omega$
则 C1=$1\times 10^{-7}F=0.1uF$
则 C2=$1\times 10^{-7}F=0.1uF$
则 R3=$19\times R_1=19\times 530.5=10.079k\Omega$
则 R2=$R_1/19=530.5/19=27.92\Omega$

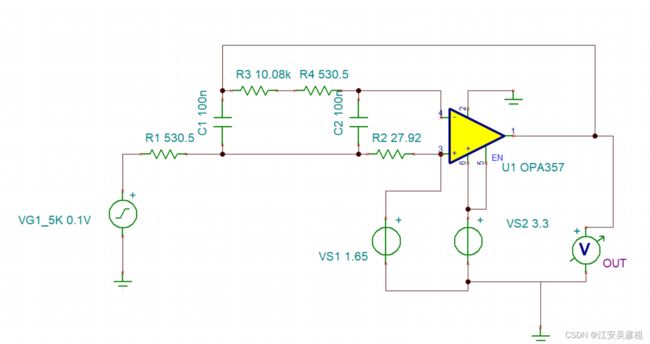
实际的电路图如下所示：

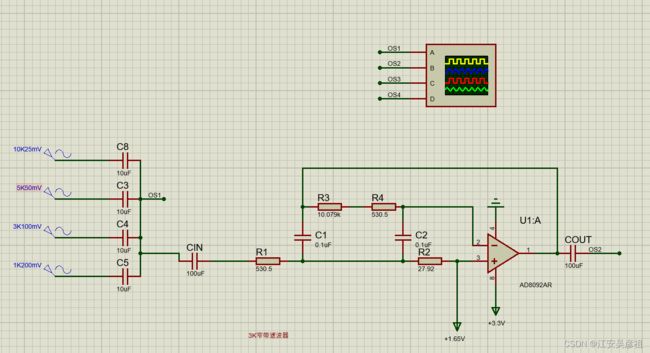
仿真效果如下：

一个横格0.2ms，则滤除出来的周期大致为0.3ms，即3KHZ。

TINA TI仿真

同样的，我们也在TINA TI上进行仿真：
电路图如下：

对于1K 0.1V的正弦信号，其响应如下：

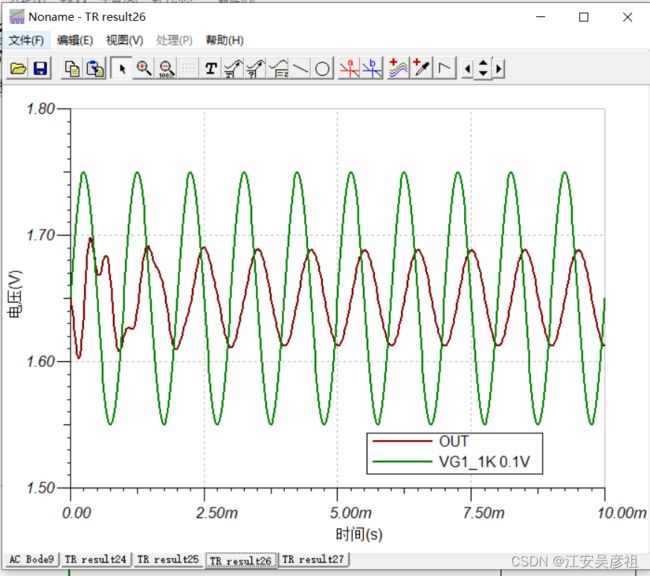
有稍微的放大作用。
对于3K的信号，其响应如下：

有将近10倍的放大作用。
对于5K信号，其响应如下：基本无放大作用。

对于10K信号，其响应如下：基本无放大作用。

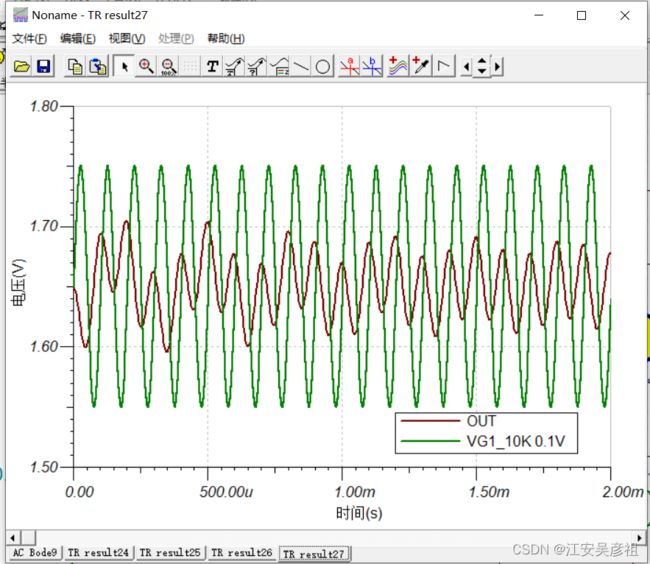
看其频率特性，如下：

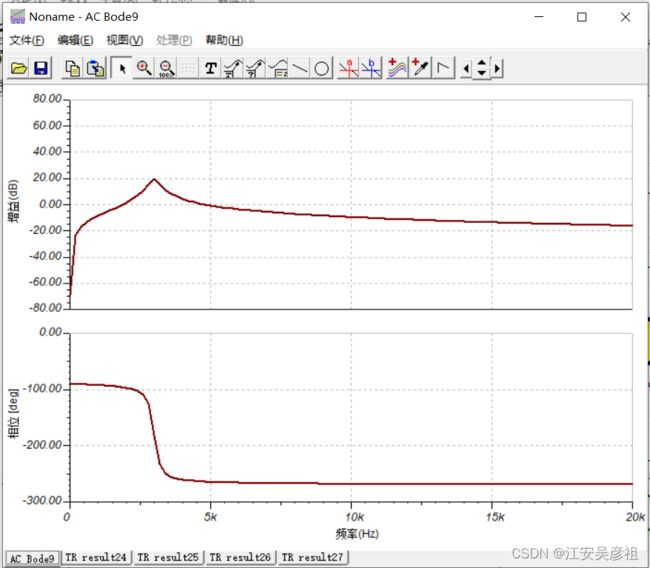
发现其有很好的窄带滤波效果。

参考

proteus 放大器仿真
赵工
Tina TI
SPICE模型
导入模型
TI官网设计资源
包含滤波器等各种电路设计资源：