深入理解PriorityQueue实现原理、及源码分析

PriorityQueue底层使用Object[]数组实现的一个最小二叉堆，来到达一个优先队列功能，是线程不安全的。它与FIFO的队列的区别在于，优先队列每次出队的元素都是优先级最高的元素。那么怎么确定哪一个元素的优先级最高呢？PriorityQueue使用二叉堆这种数据结构，用户可以自定义的Comparator来确定每次出队的元素总是队列里面最小的，而元素的大小比较方法可以由用户指定Comparator(Comparator就相当于指定优先级)，接下来我们先来看看堆这种数据结构。

1.二叉堆介绍

堆数据结构的特性

• 堆中某个节点的值总是不大于或不小于其父节点的值。

• 堆总是一棵完全二叉树。

在堆数据结构又有很多种，而PriorityQueue使用的便是二叉堆，二叉堆是一种特殊的堆，二叉堆是一颗完全二叉树或者是近似一颗完全二叉树。

(1)二叉堆分类

二叉堆分为两种：最大堆和最小堆。PriorityQueue使用的便是最小二叉堆，根的位置元素永远是最小的。

• 最大堆：父结点的键值总是大于或等于任何一个子节点的键值。

• 最小堆：父结点的键值总是小于或等于任何一个子节点的键值。

(2)二叉堆结构

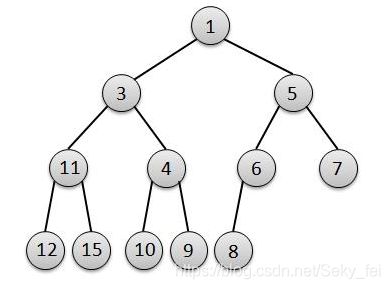
这里我们最小二叉堆为例，将一个二叉堆结构用一颗完全二叉树表示出来，各个元素位置如下图 :

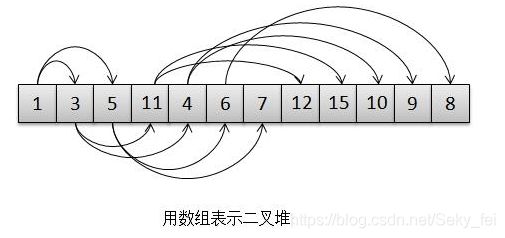
上图就是一颗完全二叉树（二叉堆），二叉堆特点：那就是在第n层深度被填满之前，不会开始填第n+1层深度，且元素插入是从左往右填满。基于这个特点我们用数据结构来表示一个二叉堆，如下图：

PriorityQueue内部实现就是使用一个Object[]数组来表示二叉堆的，基于数组实现的二叉堆结构具有以下特点：

• 跟节点：数组实现的二叉堆，根节点在index=0位置上。

• 左孩子：数组n位置上的元素，其左孩子在[2n+1]位置上。

• 右孩子：数组n位置上的元素，其右孩子在 2(n+1) 位置上。

• 父节点：数组n位置上的元素，其父节点在 (n-1)/2 位置上。

到此二叉堆的结构就了解完了，接下来在继续看看PriorityQueue是怎么实现的？

2.PriorityQueue源码分析

(1)PriorityQueue主要结构

PriorityQueue继承了AbstractQueue抽象类，并实现了Serializable接口，AbstractQueue抽象类实现了Queue接口，对元素添加、删除等方法进行了一些通用的定义。PriorityQueue的底层存储结构相关定义如下：

public class PriorityQueue extends AbstractQueue
    implements java.io.Serializable {
    private static final long serialVersionUID = -7720805057305804111L;
    // 用数组实现的二叉堆: 如前面的说法一样，左右子节点位置、父节点位置、根节点位置。
    /**
     * Priority queue represented as a balanced binary heap: the two
     * children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The
     * priority queue is ordered by comparator, or by the elements'
     * natural ordering, if comparator is null: For each node n in the
     * heap and each descendant d of n, n <= d.  The element with the
     * lowest value is in queue[0], assuming the queue is nonempty.
     */
    transient Object[] queue; // non-private to simplify nested class access
    //数组默认初始化大小 
    private static final int DEFAULT_INITIAL_CAPACITY = 11;
    //队列的元素数量
    private int size = 0;
    //自定义比较器
    private final Comparator comparator;
    //队列修改次数：修改版本
    transient int modCount = 0;
    //queue数组的最大长度，即队列的最大长度
    private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
}

可以看到PriorityQueue也是基于数组来实现一个二叉堆，PriorityQueue是一个有限队列，数据queue最大不能超过Integer.MAX_VALUE - 8，PriorityQueue中的优先级可以由用户指定，就是用户指定元素的Comparator比较器。

(2)PriorityQueue的构造方法

//1.默认构造方法:使用默认的初始11来构造一个优先队列，比较器comparator为空，这里要求入队的元素必须实现Comparator接口,不然在put元素时会抛ClassCastException
public PriorityQueue() {
    this(DEFAULT_INITIAL_CAPACITY, null);
}

//2.指定一个初始化大小来构造优先队列，比较器comparator为空，这里要求入队的元素必须实现Comparator接口
public PriorityQueue(int initialCapacity) {
    this(initialCapacity, null);
}

//3.默认初始化大小 和 指定一个comparator构造优先级队列
public PriorityQueue(Comparator comparator) {
    this(DEFAULT_INITIAL_CAPACITY, comparator);
}

//4.使用指定的初始大小和比较器来构造一个优先队列
public PriorityQueue(int initialCapacity,
                     Comparator comparator) {
    //初始大小不允许小于1
    if (initialCapacity < 1)
        throw new IllegalArgumentException();
    //使用指定初始大小创建数组
    this.queue = new Object[initialCapacity];
    //初始化比较器
    this.comparator = comparator;
}

优先级队列PriorityQueue也支持在构建的时候，将一个集合的元素初始化到该优先级队列中去。一共提供了三种构造器，如下继续分析源码。

//构造一个指定Collection集合参数的优先队列
public PriorityQueue(Collection c) {
    //判断集合c是不是SortedSet实例
    if (c instanceof SortedSet) {
        SortedSet ss = (SortedSet) c;
        //使用SortedSet集合的比较器来初始化队列的Comparator
        this.comparator = (Comparator) ss.comparator();
        //从集合中初始化数据到队列(注意：SortedSet是一个已经排好序的二叉树，所以初始化到优先级队列后不需要额外排序)
        initElementsFromCollection(ss);
    }
    //判断集合c是不是优先队列实例
    else if (c instanceof PriorityQueue) {
        PriorityQueue pq = (PriorityQueue) c;
        //使用PriorityQueue的比较器来初始化队列的Comparator
        this.comparator = (Comparator) pq.comparator();
        //从集合中初始化数据到队列(优先级队列不需要额外排序)
        initFromPriorityQueue(pq);
	}
    else {
        //其他类型的集合，元素必须实现Comparator接口，在压堆和出堆时需要将元素强转成Comparator在比较大小
    	this.comparator = null;
        //从集合c中初始化元素到队列中(优先级队列需要额外排序)
    	initFromCollection(c);
    }
}

上面构造器中initElementsFromCollection()、initFromPriorityQueue()和initFromCollection()的作用是将集合中的元素初始化到优先级队列中去，具体会涉及到堆结构的初始化。

//将元素从集合中初始化到优先级队列中
private void initElementsFromCollection(Collection c) {
    //目标队列
    Object[] a = c.toArray();
    //如果不是Object数组，则将c转换成Object数组
    if (a.getClass() != Object[].class)
        a = Arrays.copyOf(a, a.length, Object[].class);
    int len = a.length;
    if (len == 1 || this.comparator != null)
        //循环遍历check集合里面有没有为null的元素
        for (int i = 0; i < len; i++)
            if (a[i] == null)
                throw new NullPointerException();
    this.queue = a;
    this.size = a.length;
}


//如果初始化集合就是一个优先级队列，直接赋值，不需额外的堆排序操作
private void initFromPriorityQueue(PriorityQueue c) {
    if (c.getClass() == PriorityQueue.class) {
        this.queue = c.toArray();
        this.size = c.size();
    } else {
        //如果集合C不是优先级队列类型时，需要额外的最小堆排序
        initFromCollection(c);
    }
}

//初始化优先级队列object[]数组后，再额外的进行堆化(最小堆排序)
private void initFromCollection(Collection c) {
    //初始化object[]数组
    initElementsFromCollection(c);
    //堆化：最小堆排序操作（后面在详细分析）
    heapify();
}

在构造方法中，会调用initFromCollection方法将传入集合C初始化到优先队列queue后，再调用heapify方法对数组进行调整，使得它符合二叉堆的规范或者特点，具体heapify是怎么构造二叉堆的，后面再详细分析，先看看PriorityQueue的二叉堆的添加元素和删除元素的原理。

(3)PriorityQueue的入队实现

红黑树TreeMap的结构里为了维护其红黑平衡，主要有三个动作：左旋、右旋、变色。那么二叉堆为了维护他的特点又需要进行什么样的操作呢？先看看最小二叉堆的特点：

• （1）父结点的键值总是小于或等于任何一个子节点的键值。

• （2）基于数组实现的二叉堆，对于数组中任意位置的n上元素，其左孩子在[2n+1]位置上，右孩子[2(n+1)]位置，它的父亲则在[n-1/2]上，而根的位置则是[0]。

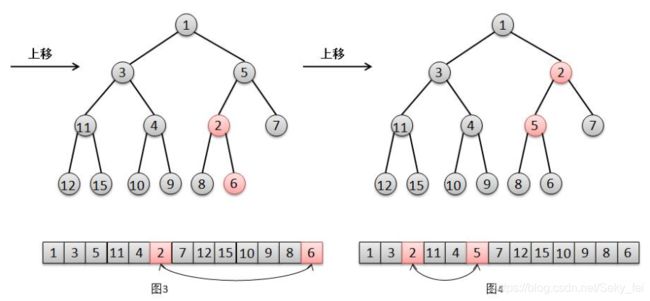
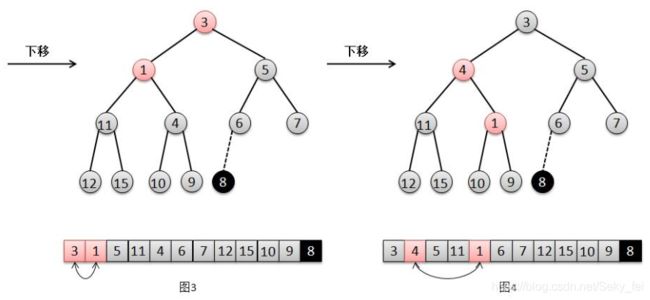
为了维护这个特点，二叉堆在添加元素的时候，需要一个"上移"的动作，那么怎么上移操作的呢？过程如下图。

结合上面的图解，说明一下二叉堆的添加元素的过程：

• （1）将元素2添加在最后一个位置（队尾）（图2）。

• （2）由于2比其父亲6要小，所以将元素2上移，交换2和6的位置（图3）。

• （3）然后由于2比5小，继续将2上移，交换2和5的位置（图4），此时2大于其父亲（根节点）1，结束。

下面我们来具体分析一下PriorityQueue入队代码的具体实现过程。

//(1)添加元素
public boolean add(E e) {
    return offer(e);
}

//(2)元素上移操作
public boolean offer(E e) {
    //添加元素不能为null，需要comparator比较元素大小
    if (e == null)
        throw new NullPointerException();
    //修改版本+1
    modCount++;
    //记录当前队列中元素的个数
    int i = size;
    //如果当前元素个数大于等于队列底层数组的长度，则进行扩容
    if (i >= queue.length)
        grow(i + 1);
    //元素个数+1
    size = i + 1;
    if (i == 0)
        //如果队列中没有元素，则将元素e直接添加至根（数组小标0的位置）
        queue[0] = e;
    else
        //否则调用siftUp方法，将元素添加到尾部，进行上移判断
        siftUp(i, e);
    return true;
}

//(3)数组扩容：添加时，元素个数大于等于队列底层数组的长度，则进行扩容。
private void grow(int minCapacity) {
    //获取队列的数组的长度
    int oldCapacity = queue.length;
    //扩容：如果oldCapacity小于64，每次扩容到2*oldCapacity + 2大小；否则扩大到3倍
    int newCapacity = oldCapacity + ((oldCapacity < 64) ?
									 (oldCapacity + 2) :
									 (oldCapacity >> 1));
    //长度溢出判断：newCapacity长度超出了最大值限制，hugeCapacity方法赋值为Integer.MAX_VALUE
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
    //扩容并拷贝元素
    queue = Arrays.copyOf(queue, newCapacity);
}

//(4)元素上移实现方法：x表示新增的元素，k表示原堆数组的长度。
private void siftUp(int k, E x) {
    if (comparator != null)
        //如果比较器comparator不为空，则调用siftUpUsingComparator方法进行上移操作
        siftUpUsingComparator(k, x);
    else
        //如果比较器comparator为空，则调用siftUpComparable方法进行上移操
        siftUpComparable(k, x);
}
//(5)元素上移操作具体实现：用户指定了comparator。(x表示新增的元素，k表示原堆数组的长度)
private void siftUpUsingComparator(int k, E x) {
    //k>0表示判断k不是根的情况下，也就是元素x有父节点
    while (k > 0) {
        //计算原数组最后一个元素的父节点位置[(n-1)/2]
        int parent = (k - 1) >>> 1;
        //取出原数组最后一个元素的父亲e
        Object e = queue[parent];
        //如果新增的元素x比最后一个元素的父亲e大，则不需要"上移"，跳出循环结束
        if (comparator.compare(x, (E) e) >= 0)
            break;
        //x比父亲小，则需要进行"上移",交换元素x和父亲e的位置
        queue[k] = e;
        //将新插入元素的位置k指向父亲的位置，进行下一层循环
        k = parent;
	}
    //找到新增元素x的合适位置k之后,进行赋值
    queue[k] = x;
}

//(6)元素上移操作具体实现：使用元素的comparator进行比较，逻辑和siftUpUsingComparator()一样
private void siftUpComparable(int k, E x) {
    Comparable key = (Comparable) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (key.compareTo((E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
}

添加元素时，二叉堆"上移"操作的代码还是很容易理解的，主要就是不断的将新增元素和其父亲进行大小比较，比父亲小则上移，最终找到一个合适的位置。中间有一个点需要注意的就是扩容问题。

(4)PriorityQueue的出队实现

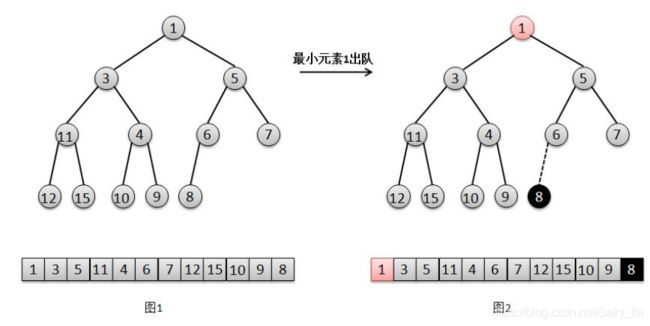
PriorityQueue的出队实现实际就是二叉堆的删除根的原理；对于二叉堆的出队操作，出队永远是删除根元素操作，也就是最小的元素，要删除根元素，就要找一个元素替代者移动到根位置，相对于被删除的元素来说就是"下移"。下移过程如下：

结合上面的图解，我们来说明一下二叉堆的出队过程:

• (1)将找出队尾的元素8，并将它在队尾位置上删除（图2）。

• (2)此时队尾元素8比根元素1的最小孩子3要大，所以将元素1下移，交换1和3的位置（图3）。

• (3)然后此时队尾元素8比元素1的最小孩子4要大，继续将1下移，交换1和4的位置（图4）。

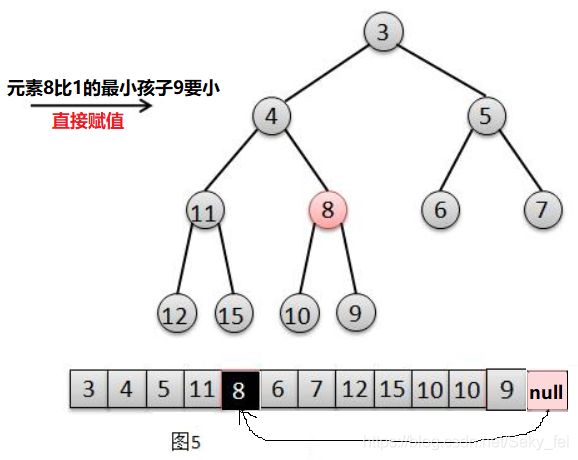
• (4)然后此时根元素8比元素1的最小孩子9要小，不需要下移，直接将根元素8赋值给此时元素1的位置，再将队尾位置值置null(图5)，结束。

下面我们来具体分析一下PriorityQueue的代码是怎么实现出队操作的。

//(1)PriorityQueue二叉堆的出队操作
public E poll() {
    //队列为空，返回null
    if (size == 0)
        return null;
    //队列元素个数-1
    int s = --size;
    //修改版本+1
    modCount++;
    //取出队头的元素
    E result = (E) queue[0];
    //取出队尾的元素
    E x = (E) queue[s];
    //将队尾元素置为null
    queue[s] = null;
    //如果队列中不止队尾一个元素，则调用siftDown方法进行"下移"操作
    if (s != 0)
        siftDown(0, x);
    return result;
}

//(2)下移操作：x表示队尾的元素，k表示被删除元素在数组的位置
private void siftDown(int k, E x) {
    if (comparator != null)
        //如果比较器comparator不为空，则调用siftDownUsingComparator方法进行下移操作
        siftDownUsingComparator(k, x);
    else
        //比较器comparator为空，则调用siftDownComparable方法进行下移操作
        siftDownComparable(k, x);
}

//(3)元素下移操作具体实现：指定comparator
private void siftDownUsingComparator(int k, E x) {
    //通过size/2找到第一个没有叶子节点的元素(根据堆父节点位子关系：父节点在 (n-1)/2位置上，堆最后一个元素的位子是size-1,则最后一个有叶子节点的元素位子是：(size-1-1)/2,所以第一个没有叶子节点的元素的位子是size/2)
    int half = size >>> 1;
    //比较位置k和half，如果k小于half，则k位置的元素就不是叶子节点
    while (k < half) {
        //找到根元素的左孩子的位置[2n+1]
        int child = (k << 1) + 1;
        //左孩子的元素
        Object c = queue[child];
        //找到根元素的右孩子的位置[2(n+1)]
        int right = child + 1;
        //如果左孩子大于右孩子，则将c赋值为右孩子的值，这里也就是找出左右孩子哪个最小
        if (right < size && comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        //如果队尾元素比根元素孩子都要小，则不需"下移"，结束。(此时就找到了尾节点x要赋值的位子)
        if (comparator.compare(x, (E) c) <= 0)
            break;
        //队尾元素比根元素孩子都大，则需要"下移"，交换跟元素和孩子c的位置
        queue[k] = c;
        //将根元素位置k指向最小孩子的位置，进入下次循环
        k = child;
    }
    //找到队尾元素x的合适位置k之后进行赋值
    queue[k] = x;
}

//(4)元素下移操作具体实现：使用元素的comparator，和siftDownUsingComparator逻辑一样
private void siftDownComparable(int k, E x) {
    Comparable key = (Comparable)x;
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
        int child = (k << 1) + 1; // assume left child is least
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            ((Comparable) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        if (key.compareTo((E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = key;
}

PriorityQueue中，不是直接将根元素删除，然后再将下面的元素做上移，重新补充根元素；而是找出队尾的元素，并在队尾的位置上删除，然后通过根元素的下移，给队尾元素找到一个合适的位置，最终覆盖掉跟元素，从而达到删除根元素的目的。这样做在一些情况下，会比直接删除在上移根元素，或者直接下移根元素再调整队尾元素的位置少操作一些步奏。

搞明白了二叉堆的入队和出队操作后，接下来我们再来看一个二叉堆中比较重要的过程：二叉堆的初始化构造。

(5)最小堆的构造过程

在前面构造函数中可以指定集合初始化到优先级队列中，提到堆的构造是通过一个heapify方法实现的，下面我们来看下heapify方法的实现。

private void heapify() {
    for (int i = (size >>> 1) - 1; i >= 0; i--)
        siftDown(i, (E) queue[i]);
}

这个方法很简单，就这几行代码，但是理解起来却不是那么容器的。具体来分析一下，假设有一个无序的数组，要求我们将这个数组建成一个二叉堆，最简单的办法当然是将数组的数据一个个取出来，调用入队方法。但是这样做，每次入队都有可能会伴随着元素的移动，这么做是十分低效的。那么有没有更加高效的方法呢，就是我问上面讲到的"下移"操作。

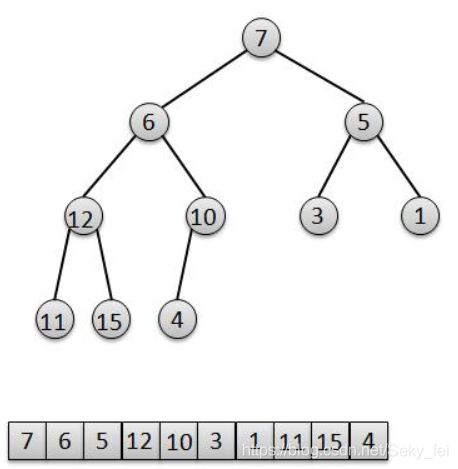
为了方便，先构建一个无序的二叉堆数组，顺序已经随机打乱，暂时不用符合最小二叉堆的标准。如下图：int a = [7, 6, 5, 12, 10, 3, 1, 11, 15, 4 ]。

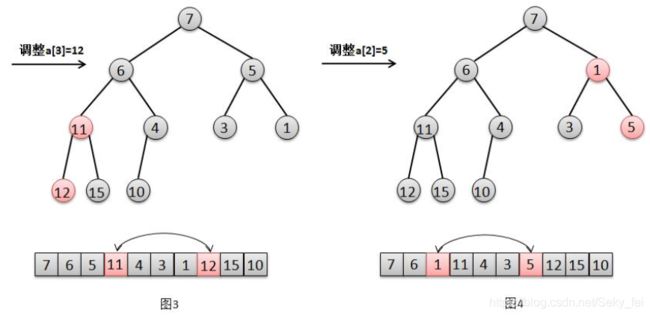
观察下用数组a建成的二叉堆，很明显，对于叶子节点4、15、11、1、3来说，它们已经是一个合法的堆。所以只要最后一个节点的父节点，也就是最后一个非叶子节点a[4]=10开始调整，然后依次调整a[3]=12，a[2]=5，a[1]=6，a[0]=7，分别对这几个节点做一次"下移"操作就可以完成了堆的构造。操作过程如下这个过程。

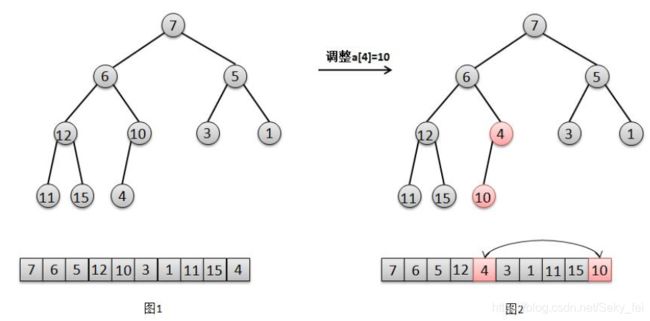
参照图解分别来解释下这几个步奏：

• （1）对于节点a[4]=10的调整（图1），只需要交换元素10和其子节点4的位置（图2）。

• （2）对于节点a[3]=12的调整，只需要交换元素12和其最小子节点11的位置（图3）。

• （3）对于节点a[2]=5的调整，只需要交换元素5和其最小子节点1的位置（图4）。

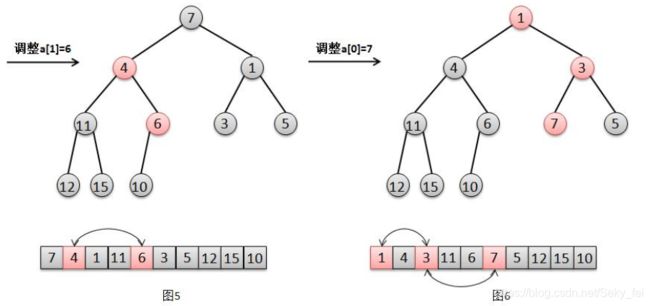
• （4）对于节点a[1]=6的调整，只需要交换元素6和其最小子节点4的位置（图5）。

• （5）对于节点a[0]=7的调整，只需要交换元素7和其最小子节点1的位置，然后交换7和其最小自己点3的位置（图6）。

至此，调整完毕，建堆完成。 再来回顾一下，PriorityQueue的建堆代码，这下就可以看得懂了。

private void heapify() {
    #(size >>> 1) - 1，这行代码是为了找寻最后一个非叶子节点，然后倒序进行"下移"siftDown操作。
    for (int i = (size >>> 1) - 1; i >= 0; i--)
        siftDown(i, (E) queue[i]);
}

#备注：最后一个非叶子节点就是数组最后一个节点的父节点，根据最好二叉堆父节点在 (n-1)/2位置上，则最后一个节点的父节点为：(size-1-1)/2 = size/2 -1

到此PriorityQueue的最小二叉堆结构重要的操作就分析完了，明白了其底层二叉堆的概念及其入队、出队、建堆等操作，其他的一些方法代码就很简单了。

 通过最近在找工作，才发现好多知识点平时都学得不深入，只是停留在皮毛上；每一次的痛苦都是成长的过程，坚持学习，持续成长，最后才能变成自己想变成的人。

                                                                             2020年08月08日 晚 于北京记