浅谈生成式模型与辨别式模型,以naive Bayes和logistic regression为例
文章目录
-
- classification
- naive Bayes
- logistic regression
- logistic regression和linear regression的异同
- 生成式vs辨别式
- 多分类
classification
我们以分类作为大背景,来看看生成式模型与辨别式模型的区别
假设你是大木博士,你有一个任务,是训练一个模型来对水属性宝可梦和一般属性宝可梦进行二分类
我们的类别集合为 C = { C 1 , C 2 } C=\{C_1,C_2\} C={C1,C2},其中 C 1 C_1 C1为水系宝可梦, C 2 C_2 C2为一般系宝可梦,我们已知的是样本集合 x ∈ X , x ∈ R n x∈X,x∈R^n x∈X,x∈Rn的数目为: C 1 = 79 C_1=79 C1=79, C 2 = 61 C_2=61 C2=61,如果我们现在只取每只宝可梦的攻击和防御两个特征,则 x ∈ R 2 x∈R^2 x∈R2
那么,我们要如何利用这组样本来对宝可梦们进行属性分类呢?
naive Bayes
首先我们来看看如何利用朴素贝叶斯模型来进行二分类
朴素贝叶斯满足假设:样本x的每个特征(攻击力,防御力)之间相互独立
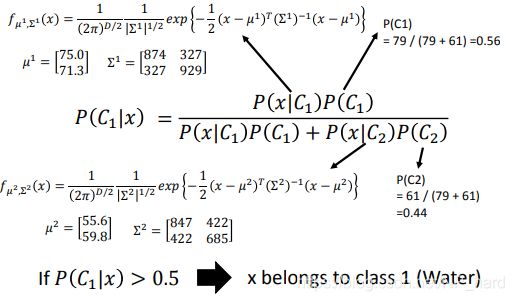
我们先看看贝叶斯公式 P ( C 1 ∣ x ) = P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 1 ) P ( C 1 ) + P ( x ∣ C 2 ) P ( C 2 ) P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)} P(C1∣x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x∣C1)P(C1)
其中
P ( C 1 ) , P ( C 2 ) P(C_1),P(C_2) P(C1),P(C2)为先验概率,我们可以通过 P ( C 1 ) = 79 79 + 61 , P ( C 1 ) = 61 79 + 61 P(C_1)=\frac{79}{79+61},P(C_1)=\frac{61}{79+61} P(C1)=79+6179,P(C1)=79+6161来进行计算
P ( x ∣ C 1 ) , P ( x ∣ C 2 ) P(x|C_1),P(x|C_2) P(x∣C1),P(x∣C2)为似然,即我们从样本集合中,随便抽一只宝可梦,这只宝可梦是水系/一般系的概率,通常我们根据样本的性质来假设样本的分布,这是朴素贝叶斯的核心,也是生成式模型的核心,就是样本的分布是我们假设出来的,可以理解为样本的分布是模型“脑补出来的”,我们在后面会仔细讲解
关于概率的先验,后验,如果不太熟悉话,可以看看我的这篇blog
如果我们知道以上四个概率的值,我们就可以直接通过贝叶斯公式计算出 P ( C ∣ x ) P(C|x) P(C∣x)了
x = { 水 属 性 P ( C 1 ∣ x ) > 0.5 一 般 属 性 e l s e x=\begin{cases} 水属性&P(C_1|x)>0.5\\ 一般属性&else \end{cases} x={水属性一般属性P(C1∣x)>0.5else
至于似然要取什么样的分布,是取决于x的性质的
- x是连续的,取高斯分布
- x是稀疏离散的,即x=1或x=0,取伯努利分布
- …
在这里我们取高斯分布作为似然 P ( C ∣ x ) P(C|x) P(C∣x)的分布
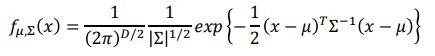
ok,既然已经确定了似然,那我们该如何求解贝叶斯公式呢?我们还有什么未知的参数吗?
对了,高斯分布的似然的参数 μ 1 , μ 2 , Σ 1 , Σ 2 \mu_1,\mu_2,\Sigma_1,\Sigma_2 μ1,μ2,Σ1,Σ2我们还不知道呢?
由于贝叶斯假设,样本x的各个特征相互独立,假设x只有两个特征,我们可以用两个一维高斯分布来作为 x 1 , x 2 x_1,x_2 x1,x2的似然分布
我们采用极大似然法来求以上的参数 μ 1 , μ 2 , Σ 1 , Σ 2 \mu_1,\mu_2,\Sigma_1,\Sigma_2 μ1,μ2,Σ1,Σ2
似然函数的形式十分简单,下式为 P ( C 1 ∣ x ) P(C_1|x) P(C1∣x)的似然函数
![]()
具体求解过程这里就不展开了 ,感兴趣的可以参考我关于naive Bayes的公式推导
ok,如下图所示,我们很轻易的得到了两种属性的高斯分布的参数,对于输入x,我们可以使用朴素贝叶斯模型对其进行分类了
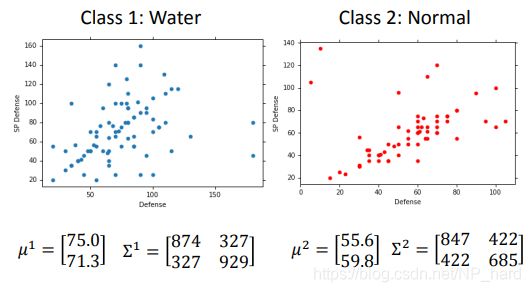
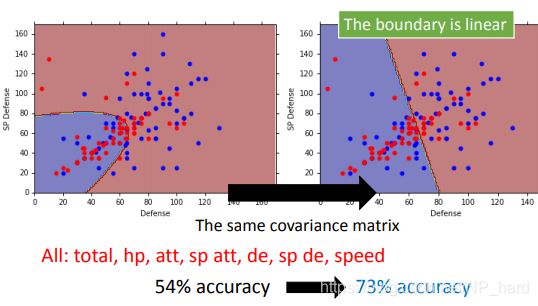
如下图所示,红点为水属性宝可梦,蓝点为一般系宝可梦,我们根据output的 P ( C 1 ∣ x ) = 0 P(C_1|x)=0 P(C1∣x)=0画出决策界限,最后发现准确率相当糟糕 ,我艹了
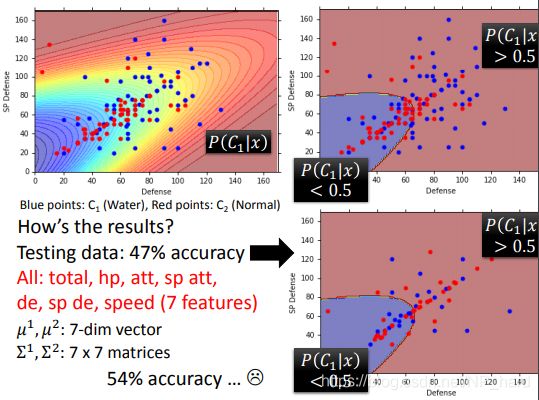
一开始我觉得是因为特征太少,如果在高维空间说不定能把样本分开,后面尝试了一下发现准确率并没有提升太多
后面我考虑让x的两个特征的高斯分布共用同一个协方差矩阵,这样可以减少参数的个数,现在的参数列表为 μ 1 , μ 2 , Σ \mu_1,\mu_2,\Sigma μ1,μ2,Σ,这样可以有效防止过拟合
当然,此时还是满足贝叶斯假设,尽管这两个高斯分布共用同一个协方差矩阵,但它们的均值不同,还是两个独立的分布
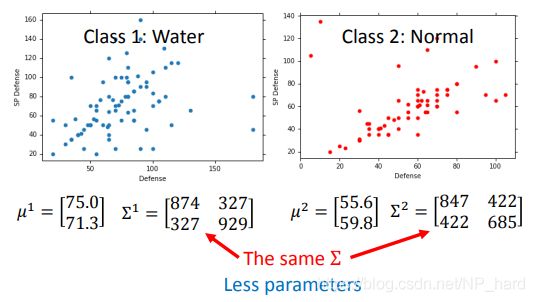
此时我们求解的最大似然函数为

改进后的模型一下子就变的强劲了许多,准确率得到了提升
诶,但是决策界限怎么变成了直线呢? 埋个坑,和logistic regression有关哦
logistic regression
我们的朴素贝叶斯模型的后验概率,即 P ( C 1 ∣ x ) P(C_1|x) P(C1∣x),可以经过一系列的数学推导,转换为 P ( C 1 ∣ x ) = σ ( z ) , z = l n P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 2 ) P ( C 2 ) P(C_1|x)=\sigma(z),z=ln\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)} P(C1∣x)=σ(z),z=lnP(x∣C2)P(C2)P(x∣C1)P(C1)

下面为一些数学推导,不喜勿入




最后的结论就是 z = w T x + b z=w^Tx+b z=wTx+b

所以 P ( C 1 ∣ x ) = σ ( z ) , z = w T x + b P(C_1|x)=\sigma(z),z=w^Tx+b P(C1∣x)=σ(z),z=wTx+b
龟龟,那我们干嘛还求 μ 1 , μ 2 , Σ \mu_1,\mu_2,\Sigma μ1,μ2,Σ,直接求 w , b w,b w,b不就完事了
这样想法就是辨别式模型
logistic regression
f w , b ( x ) = P w , b ( C 1 ∣ x ) f_{w,b}(x)=P_{w,b}(C_1|x) fw,b(x)=Pw,b(C1∣x)
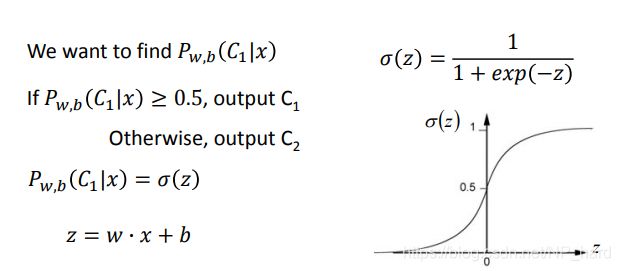
logistic regression和linear regression的异同
首先是开门见山,下图为两者的对比

我们可以发现,logistic和linear大致相同,就是它们的loss fuction不同
- logistic L ( f ) = ∑ n C ( f ( x n ) , y ^ n ) L(f)=\sum_{n}C(f(x^n),\hat y^n) L(f)=∑nC(f(xn),y^n),cross entropy
- linear ( f ( x n ) − y ^ n ) 2 (f(x^n)-\hat y^n)^2 (f(xn)−y^n)2,square error
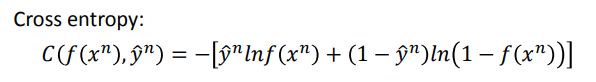
logistic regression的loss function推导
这是我们的训练样本

假设我们的样本都是 C 1 C_1 C1的高斯分布生成的
f w , b ( x ) = P w , b ( C 1 ∣ x ) f_{w,b}(x)=P_{w,b}(C_1|x) fw,b(x)=Pw,b(C1∣x)
则它们的似然函数为
![]()
我们要找到 w ∗ , b ∗ w^*,b^* w∗,b∗,使得似然函数最大
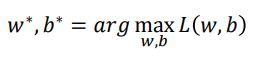

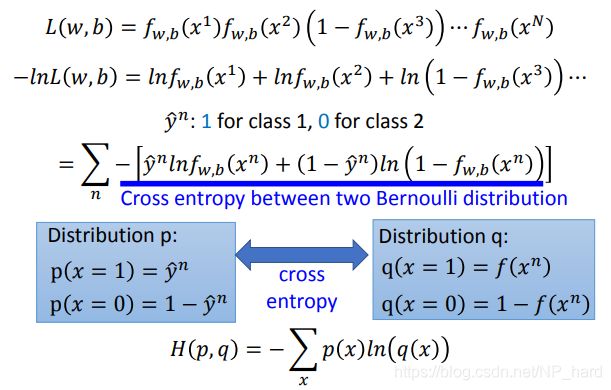
经过一系列的推导与转化,我们得到了logistic的loss function,为
L ( f ) = ∑ n C ( f ( x n ) , y ^ n ) L(f)=\sum_{n}C(f(x^n),\hat y^n) L(f)=n∑C(f(xn),y^n)
![]()
cross entropy表示的是两个分布之间的相似程度
有了loss function,我们就可以计算梯度并进行迭代更新
从下图我们可以看到,logistic的下降速度,也就是梯度的大小,取决于分布 f w , b ( x n ) f_{w,b}(x^n) fw,b(xn)与 y ^ n \hat y^n y^n的相似程度,它们越不相似,梯度就越大,下降的速度也就越快,反之同理
我们最后会惊奇的发现,logistic和linear的迭代方程是一模一样的
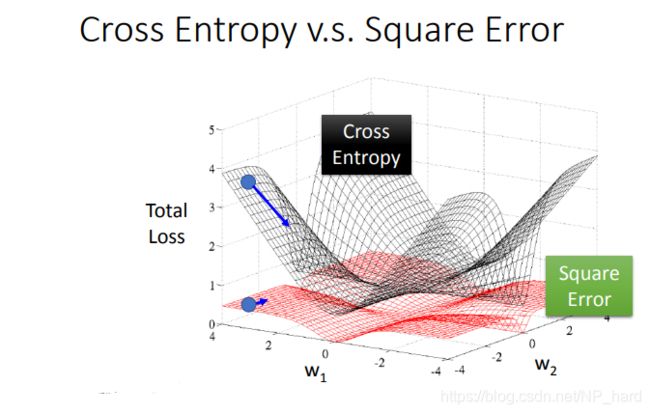
那么,为什么logistic不用square error作为loss fuction,而是要用cross entropy呢?
通过下面两张图的推导,我们发现
当logistic使用square error作为loss function时,梯度很小,几乎为0
生成式vs辨别式
下图为辨别式模型与生成式模型的参数选择上的区别,另外,即使使用相同的数据,相同的模型,但是生成式模型和辨别式模型生成的假设函数的参数式不同的

从下图我们可以看出辨别式模型的准确率要高于生成式模型,但这并不意味着辨别式模型就一定要比生成式模型要好

- 由于生成式模型会自己“脑补”(有假设分布),故生成式模型所需的训练数据会较少
- 由于生成式模型会假设分布,所以它对抗噪声干扰的能力会更强
- 生成式模型的计算可以拆为prior(先验)和class-dependent probabilities(似然),而先验和似然可以来自不同的源(例如语音识别)
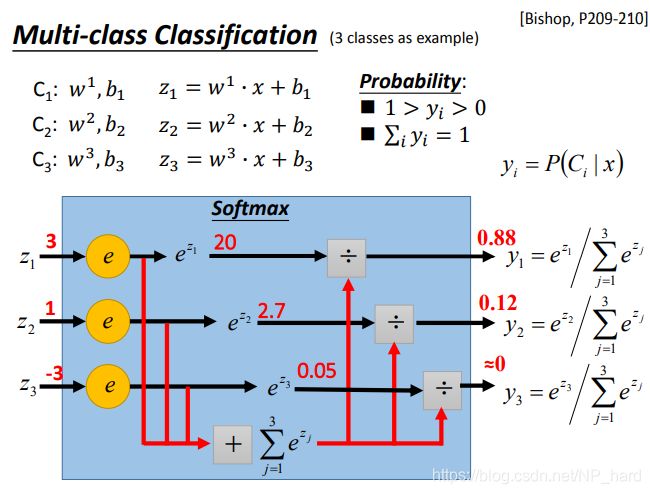
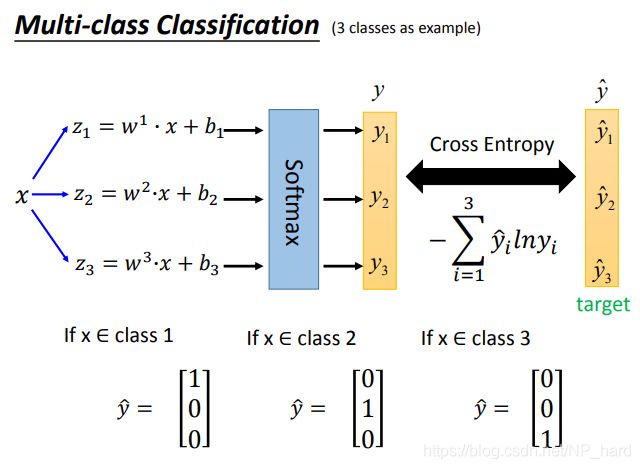
多分类
softmax可以拉大z之间的差距,并且会把它们限制到0-1