快排的递归实现
快速排序是一种时间复杂度低，但会虽随着数组的顺序变化，因为其效率之高被称为快速排序，而
且其不稳定性也可以同过优化进行解决。
快速排序的实现有三种方法：
1.hoare版
其基本思想为：任取待排序元素序列中 的某元素作为基准值，按照该排序码将待排序集合分割成
两子序列，左子序列中所有元素均小于基准值，右 子序列中所有元素均大于基准值，然后最左右
子序列重复该过程，直到所有元素都排列在相应位置上为止。
实现方法如图：
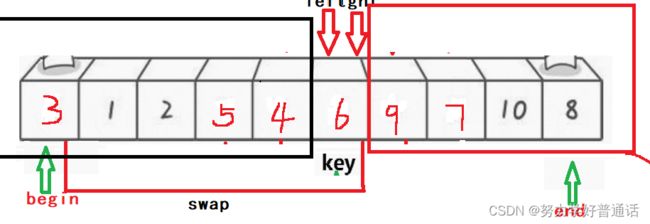
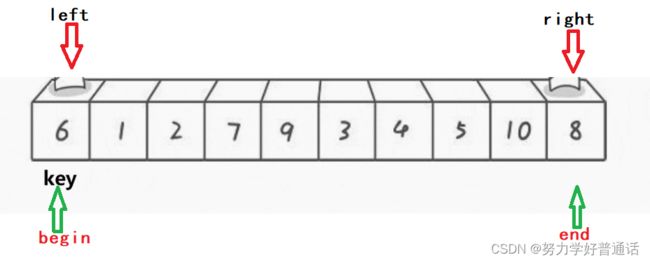这幅图是将最左端的元素定为基准值， 先让基准值的另一边（right）开始走，找到比基准值小的
元素时停下，再让基准值（left）这一边开始走，找到比基准值大的元素停下，再将right和left对应
的元素进行交换，重复上述操作。如下图：
第一次交换：
第二次交换：
第二次交换后，right先走后left与right相遇，将相遇的位置的元素与key的元素进行交换，此时
key的元素到了其排序好的最终元素的位置。 如下图：
这就是快速排序的单趟排序， 从上述图可以看出key将这个数组分为两部分，而左边和右边有可以
看为一个新的要排序的数组，而这又可以引用单趟排序，从而构成递归。
那么递归结束的条件是什么呢？是当（left == right）的时候吗？
当要拍序的数组本身有序的时候，我们会发现，可能会存在（left > right），所以递归结束的条件
应该为（left >= right）。
整体的代码如下：
//hoare法
int PartSort1(int* a, int left, int right)
{
随机选k
//int randi = left + (rand() % (right - left));
//int key = left;
//三数取中法
int mid = FindMidNumi(a, left, right);
if (mid != left)
{
Swap(&a[mid], &a[left]);
}
int key = left;
while (left < right)
{
//右边找小
while (left < right && a[right] >= a[key])
{
right--;
}
//左边找大
while (left < right && a[left] <= a[key])
{
left++;
}
Swap(&a[right], &a[left]);
}
Swap(&a[key], &a[right]);
key = right;
return key;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int key = PartSort1(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
2.挖坑法
此方法是hoare的一种变形，与上面的方法十分类似。
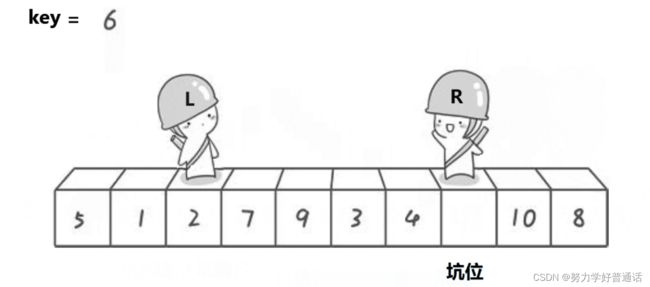
同样，我们把最左边的元素设为基准值，并将元素挖出来，用局部变量key将其存储如下图：
之后也是从右边先找到比key小的元素，并将此元素与坑位进行交换：
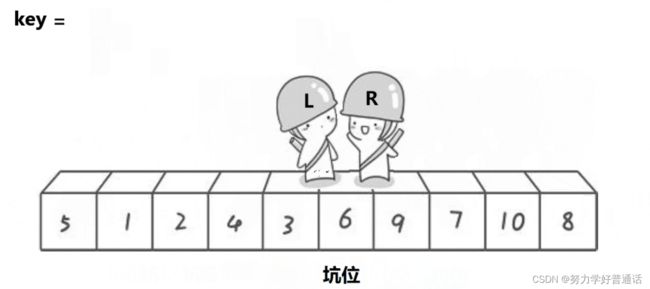
在从左边开始找比key大的元素，将其与坑位交换：
直到left与right相遇， 将key的值填回坑位。
从上述图可以看出key将这个数组分为两部分，而左边和右边有可以看为一个新的要排序的数组，
而这又可以引用单趟排序，从而构成递归。
递归结束条件为：（left >= right）。
代码如下：
//挖坑法
int PartSort2(int* a, int left, int right)
{
//三数取中法
int mid = FindMidNumi(a, left, right);
if (mid != left)
{
Swap(&a[mid], &a[left]);
}
int key = a[left];
int hole = left;
while (left < right)
{
//右边找小
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
//左边找大
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int key = PartSort2(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}3.前后指针法：
前后指针法是快排的一种进阶方法：
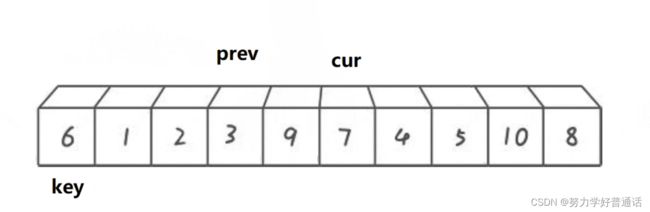
分为两个指针：一个是当前位置（cur）一个是前一个位置（prev），其排序方法如下：
同样，我们把最左边的元素设为基准值
1，如果cur的值比key小，++prev，并将cur1的元素和prev的元素进行交换，++cur。
2，如果cur的值比key大，++cur。
3，当cur超过数组范围后，将prev的值和key交换。
从上述图可以看出key将这个数组分为两部分，而左边和右边有可以看为一个新的要排序的数组，
而这又可以引用单趟排序，从而构成递归。
递归结束条件为：（left >= right）。
代码如下：
int PartSort3(int* a, int left, int right)
{
// 三数取中法
int mid = FindMidNumi(a, left, right);
if (mid != left)
{
Swap(&a[mid], &a[left]);
}
int keyi = left;
int prev = left;
int cur = left + 1;
/*while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[cur], &a[prev]);
++cur;
}
else
{
++cur;
}
}*/
//更简明，但是不好懂
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}我们刚开始提到时间复杂度随着数组的顺序变化，是因为当快速排序排有序的数组时，应为本身
就在最终位置，所以导致快排需要将所有元素都遍历一遍，从而使时间复杂度升高，而我们的解
决办法是三数取中法：
取数组最左，最右，中间三个元素来进行比较，取出最中间的元素，将其与最左边的元素进行交
换，从而使key的值在数组中处在一个居中的位置，代码如下（前面的代码都加了三数取中法）：
//三数取中法
int FindMidNumi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] > a[mid])
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
else
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
}这样就可以让快排的时间复杂度稳定在O（n*logn）了，快排还是有些难度的，不过上述方法大家
可以只掌握一种，会写出快速排序即可。