CF286-D

 

D. Mr. Kitayuta's Technology

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

 

Shuseki Kingdom is the world's leading nation for innovation and technology. There are n cities in the kingdom, numbered from 1 to n.

Thanks to Mr. Kitayuta's research, it has finally become possible to construct teleportation pipes between two cities. A teleportation pipe will connect two cities unidirectionally, that is, a teleportation pipe from city x to city y cannot be used to travel from city y to city x. The transportation within each city is extremely developed, therefore if a pipe from city x to city y and a pipe from city y to city z are both constructed, people will be able to travel from city x to city z instantly.

Mr. Kitayuta is also involved in national politics. He considers that the transportation between the m pairs of city (a_i, b_i) (1 ≤ i ≤ m) is important. He is planning to construct teleportation pipes so that for each important pair (a_i, b_i), it will be possible to travel from city a_i to city b_i by using one or more teleportation pipes (but not necessarily from city b_i to city a_i). Find the minimum number of teleportation pipes that need to be constructed. So far, no teleportation pipe has been constructed, and there is no other effective transportation between cities.

 

Input

The first line contains two space-separated integers n and m (2 ≤ n ≤ 10⁵, 1 ≤ m ≤ 10⁵), denoting the number of the cities in Shuseki Kingdom and the number of the important pairs, respectively.

The following m lines describe the important pairs. The i-th of them (1 ≤ i ≤ m) contains two space-separated integers a_i and b_i (1 ≤ a_i, b_i ≤ n, a_i ≠ b_i), denoting that it must be possible to travel from city a_i to city b_i by using one or more teleportation pipes (but not necessarily from city b_i to city a_i). It is guaranteed that all pairs (a_i, b_i) are distinct.

 

Output

Print the minimum required number of teleportation pipes to fulfill Mr. Kitayuta's purpose.

 

Sample test(s)

input

4 5
1 2
1 3
1 4
2 3
2 4

output

3

input

4 6
1 2
1 4
2 3
2 4
3 2
3 4

output

4

 

Note

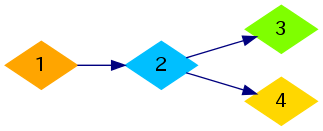
For the first sample, one of the optimal ways to construct pipes is shown in the image below:

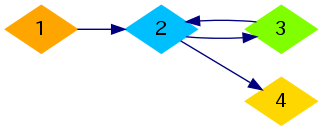
For the second sample, one of the optimal ways is shown below:

 

比较综合的一道题目...题意是在一个有向图中给出点的数目和一些点对的可达条件,求最少可以使用多少条边来满足这些条件

比如题目给出一个条件1 2,即1可达2,那么可以用一条边1->2来满足,或者用1->3,3->2两条边来满足但是这样可以新多出两个可达点对即 1 3,3 2

思路:首先如果一个包含n个点无环的连通图,那么至少得需要n-1条边来构造.如果一个包含n个点有环的连通图,那么我们可以用n条边来构造一个首尾相连

的环图,这样所有点之间都可达.至此对于一个包含n个点的连通图而言,所需最少边数不是n-1就是n,取决于该图是否有环

如果给出的不只是一个连通图呢？好,我们可以根据公式k=n-x+y来确定所需的最少边数,其中k是最少需要的边数,x是连通图的数量,y是环的数量

对于一个连通图我们只需要确定是否有环,而不用确定有多少个环,那么y<=x.

至此思路已经明确:1.将所有点划分至各个连通图当中(求连通数) 2.对各个连通分量进行判断是否有环(求环数)

对于1我们可以用dfs来遍历无向图来划分点.

对于2我们得出划分后,对各个连通图进行拓扑排序,可以判断是否有环.

 

#include <iostream>

#include <vector>

#include <queue>

using namespace std;

int indegree[100100];

int outdegree[100100];

int use[100100];

int use2[100100];

vector<int> graph[100100];

vector<int> graph2[100100];

vector<int> G[100100];

int num=0;

queue<int> q;

void dfs(int v)

{

    for(int i=0;i<graph2[v].size();i++)

    {

        if(use[graph2[v].at(i)]==0)

        {

            use[graph2[v].at(i)]=1;

            G[num].push_back(graph2[v].at(i));

            dfs(graph2[v].at(i));

        }

    }

}

int main()

{

    int n,m;

    cin>>n>>m;

    for(int i=1;i<=m;i++)

    {

        int u,v;

        cin>>u>>v;

        graph[u].push_back(v);

        graph2[u].push_back(v);

        graph2[v].push_back(u);

        indegree[v]++;

        outdegree[u]++;

    }



    for(int i=1;i<=n;i++)

    {

        if(!use[i])

        {

            num++;

            use[i]=1;

            G[num].push_back(i);

            dfs(i);

        }

    }

    int res2=0;

    for(int i=1;i<=num;i++)

    {

        queue<int> q;

        for(int j=0;j<G[i].size();j++)

        {

            if(indegree[G[i].at(j)]==0)

            {

                q.push(G[i].at(j));

            }

        }

        while(!q.empty())

        {

            int k=q.front();

            q.pop();

            use2[k]=1;

            for(int j=0;j<graph[k].size();j++)

            {

                indegree[graph[k].at(j)]--;

                outdegree[k]--;

                if(indegree[graph[k].at(j)]==0&&!use2[graph[k].at(j)])

                {

                    q.push(graph[k].at(j));

                }

            }

        }

        for(int j=0;j<G[i].size();j++)

        {

            if(use2[G[i].at(j)]==0)

            {

                res2++;

                break;

            }

        }

    }

    cout<<n-num+res2<<endl;

    return 0;

}