Computational Methods in Bayesian Analysis
About the author
This notebook was forked from this project . The original author is Chris Fonnesbeck, Assistant Professor of Biostatistics. You can follow Chris on Twitter @fonnesbeck .
Introduction
For most problems of interest, Bayesian analysis requires integration over multiple parameters, making the calculation of a posterior intractable whether via analytic methods or standard methods of numerical integration.
However, it is often possible to approximate these integrals by drawing samples from posterior distributions. For example, consider the expected value (mean) of a vector-valued random variable x:
where k (dimension of vector x) is perhaps very large.
If we can produce a reasonable number of random vectors {xi}, we can use these values to approximate the unknown integral. This process is known as Monte Carlo integration . In general, Monte Carlo integration allows integrals against probability density functions
to be estimated by finite sums
where xi is a sample from f. This estimate is valid and useful because:
-
I^→I with probability 1 by the strong law of large numbers ;
-
simulation error can be measured and controlled.
Example (Negative Binomial Distribution)
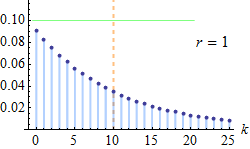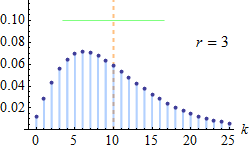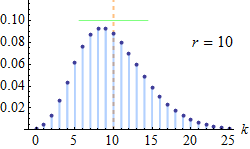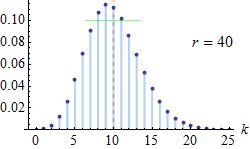
We can use this kind of simulation to estimate the expected value of a random variable that is negative binomial-distributed. The negative binomial distributionapplies to discrete positive random variables. It can be used to model the number of Bernoulli trials that one can expect to conduct until r failures occur.
The probability mass function reads
where k∈{0,1,2,…} is the value taken by our non-negative discrete random variable and p is the probability of success ($0
Most frequently, this distribution is used to model overdispersed counts , that is, counts that have variance larger than the mean (i.e., what would be predicted under aPoisson distribution ).
In fact, the negative binomial can be expressed as a continuous mixture of Poisson distributions, where a gamma distributions act as mixing weights:
where the parameters of the gamma distribution are denoted as (shape parameter, inverse scale parameter).
Let's resort to simulation to estimate the mean of a negative binomial distribution withp=0.7 and r=3:
import numpy as np r = 3 p = 0.7
# Simulate Gamma means (r: shape parameter; p / (1 - p): scale parameter). lam = np.random.gamma(r, p / (1 - p), size=100)
# Simulate sample Poisson conditional on lambda. sim_vals = np.random.poisson(lam)
The actual expected value of the negative binomial distribution is rp/(1−p), which in this case is 7. That's pretty close, though we can do better if we draw more samples:
lam = np.random.gamma(r, p / (1 - p), size=100000) sim_vals = np.random.poisson(lam) sim_vals.mean()
This approach of drawing repeated random samples in order to obtain a desired numerical result is generally known as Monte Carlo simulation .
Clearly, this is a convenient, simplistic example that did not require simuation to obtain an answer. For most problems, it is simply not possible to draw independent random samples from the posterior distribution because they will generally be (1) multivariate and (2) not of a known functional form for which there is a pre-existing random number generator.
However, we are not going to give up on simulation. Though we cannot generally draw independent samples for our model, we can usually generate dependent samples, and it turns out that if we do this in a particular way, we can obtain samples from almost any posterior distribution.
Markov Chains
A Markov chain is a special type of stochastic process . The standard definition of a stochastic process is an ordered collection of random variables:
where t is frequently (but not necessarily) a time index. If we think of Xt as a state Xat time t, and invoke the following dependence condition on each state:
then the stochastic process is known as a Markov chain. This conditioning specifies that the future depends on the current state, but not past states. Thus, the Markov chain wanders about the state space, remembering only where it has just been in the last time step.
The collection of transition probabilities is sometimes called a transition matrix when dealing with discrete states, or more generally, a transition kernel .
It is useful to think of the Markovian property as mild non-independence .
If we use Monte Carlo simulation to generate a Markov chain, this is called Markov chain Monte Carlo , or MCMC. If the resulting Markov chain obeys some important properties, then it allows us to indirectly generate independent samples from a particular posterior distribution.
Why MCMC Works: Reversible Markov Chains
Markov chain Monte Carlo simulates a Markov chain for which some function of interest (e.g., the joint distribution of the parameters of some model) is the unique, invariant limiting distribution. An invariant distribution with respect to some Markov chain with transition kernel Pr(y∣x) implies that:
∫xPr(y∣x)π(x)dx=π(y).Invariance is guaranteed for any reversible Markov chain. Consider a Markov chain in reverse sequence: {θ(n),θ(n−1),...,θ(0)}. This sequence is still Markovian, because:
Pr(θ(k)=y∣θ(k+1)=x,θ(k+2)=x1,…)=Pr(θ(k)=y∣θ(k+1)=x)Forward and reverse transition probabilities may be related through Bayes theorem:
Pr(θ(k+1)=x∣θ(k)=y)π(k)(y)π(k+1)(x)Though not homogeneous in general, π becomes homogeneous if:
n→∞
π(i)=π for some $i
If this chain is homogeneous it is called reversible, because it satisfies thedetailed balance equation :
π(x)Pr(y∣x)=π(y)Pr(x∣y)Reversibility is important because it has the effect of balancing movement through the entire state space. When a Markov chain is reversible, π is the unique, invariant, stationary distribution of that chain. Hence, if π is of interest, we need only find the reversible Markov chain for which π is the limiting distribution. This is what MCMC does!
Gibbs Sampling
The Gibbs sampler is the simplest and most prevalent MCMC algorithm. If a posterior has k parameters to be estimated, we may condition each parameter on current values of the other k−1 parameters, and sample from the resultant distributional form (usually easier), and repeat this operation on the other parameters in turn. This procedure generates samples from the posterior distribution. Note that we have now combined Markov chains (conditional independence) and Monte Carlo techniques (estimation by simulation) to yield Markov chain Monte Carlo.
Here is a stereotypical Gibbs sampling algorithm:
-
Choose starting values for states (parameters): θ=[θ(0)1,θ(0)2,…,θ(0)k].
-
Initialize counter j=1.
-
Draw the following values from each of the k conditional distributions:
θ(j)1θ(j)2θ(j)3⋮θ(j)k−1θ(j)k∼∼∼∼∼π(θ1|θ(j−1)2,θ(j−1)3,…,θ(j−1)k−1,θ(j−1)k)π(θ2|θ(j)1,θ(j−1)3,…,θ(j−1)k−1,θ(j−1)k)π(θ3|θ(j)1,θ(j)2,…,θ(j−1)