【Tsinghua OJ】灯塔(LightHouse)问题
描述
海上有许多灯塔,为过路船只照明。从平面上看,海域范围是[1, 10^8] × [1, 10^8] 。
(图一)
如图一所示,每个灯塔都配有一盏探照灯,照亮其东北、西南两个对顶的直角区域。探照灯的功率之大,足以覆盖任何距离。灯塔本身是如此之小,可以假定它们不会彼此遮挡。
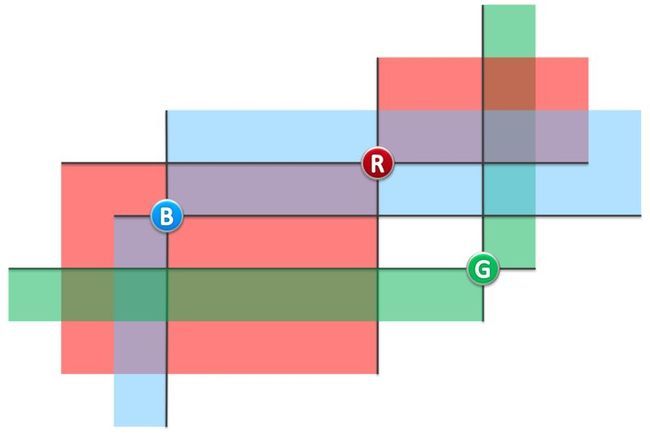
(图二)
若灯塔A、B均在对方的照亮范围内,则称它们能够照亮彼此。比如在图二的实例中,蓝、红灯塔可照亮彼此,蓝、绿灯塔则不是,红、绿灯塔也不是。
现在,对于任何一组给定的灯塔,请计算出其中有多少对灯塔能够照亮彼此。
输入
共n+1行。
第1行为1个整数n,表示灯塔的总数。
第2到n+1行每行包含2个整数x, y,分别表示各灯塔的横、纵坐标。
输出
1个整数,表示可照亮彼此的灯塔对的数量。
输入样例
3
2 2
4 3
5 1
输出样例
1
限制
对于90%的测例:1 ≤ n ≤ 3×105
对于95%的测例:1 ≤ n ≤ 106
全部测例:1 ≤ n ≤ 4×106
灯塔的坐标x, y是整数,且不同灯塔的x, y坐标均互异
1 ≤ x, y ≤ 10^8
提醒
注意机器中整型变量的范围,C/C++中的int类型通常被编译成32位整数,其范围为[-231, 231 - 1],不一定足够容纳本题的输出。
时间:2s,内存:256MB
【solution】
很容易的,我们能将这道题和逆序对联系起来。
原因在于A和B能够相互照亮的条件(假设A(x)<B(x))就是B在A的右上方。注意原题注明了:不同灯塔的x, y坐标均互异。
所以只要我们首先将所有点按照x坐标排序,接下来在y坐标中统计所有“非逆序对”或者说“顺序对”,再求和,就可以了。
而问题的关键就在于在这样的数据规模下如何快速的统计出“顺序对”的个数。
如果只是单纯的O(n^2)的算法显然是效率不够的。
那,如何从向量中快速的统计出“顺序对”的个数?
这里大概思考之后可以联想到 归并排序。
归并排序的关键也就是用分治的策略,将原问题一分为二的递归下去,最后的关键步骤只是将左右两个有序的区间合并起来即可。
而很快会发现,在合并的过程中似乎我们就可以顺便统计“顺序对”的个数。
考虑这样的一种情形:
目前左右两个有序区间,分别有指针 i, j 指向该区间下一个要合并的元素。
当a[i] < a[j]的时候(不可能相等,原题目已经说明),此时 a[i] 就要被合并。
而 a[j] 以及所有右区间大于 a[j] 的元素 其实都与 a[i] 构成“顺序对”。
统计完后,i 指向 i++ 的元素,且区间也都是没有重叠部分的,所以也并不会重复计数。
这样在归并排序合并的同时,也将所有的“顺序对”无重复无遗漏地记录了下来。
算法复杂度也就是O(nlogn)的。
源码如下:
1 #include <stdio.h> 2 3 #define L 1000005 4 5 int y[L], le[L], ri[L]; 6 long ans = 0; 7 8 void qsort(int a[], int b[], int l, int r) 9 { 10 int i, j, x, t; 11 i = l; j = r; x = a[i + ((j - i)>>1)]; 12 do 13 { 14 while (x > a[i]) i++; 15 while (x < a[j]) j--; 16 if (i <= j) 17 { 18 t = a[i]; a[i] = a[j]; a[j] = t; 19 t = b[i]; b[i] = b[j]; b[j] = t; 20 i++; j--; 21 } 22 } while (i <= j); 23 if (i < r) qsort(a, b, i, r); 24 if (j > l) qsort(a, b, l, j); 25 } 26 27 void Merge(int l, int mi, int r) 28 { 29 int i, j, k, n1 = mi - l + 1, n2 = r - mi; 30 const int MAX = 100000005; 31 32 for (i = 1; i <= n1; i++) le[i] = y[l + i - 1]; 33 for (i = 1; i <= n2; i++) ri[i] = y[mi + i]; 34 35 le[n1 + 1] = MAX; ri[n2 + 1] = MAX; 36 37 i = 1; j = 1; 38 for (k = l; k <= r; k++) 39 { 40 if (le[i] > ri[j]) y[k] = ri[j++]; 41 else 42 { 43 y[k] = le[i++]; 44 ans += long(n2) - j + 1; 45 } 46 } 47 48 49 } 50 51 void Merge_Sort(int l, int r) 52 { 53 int mi; 54 if (l == r) return; 55 mi = l + ((r - l)>>1); 56 Merge_Sort(l, mi); 57 Merge_Sort(mi + 1, r); 58 Merge(l, mi, r); 59 } 60 61 int main(void) 62 { 63 int n, x[L]; 64 scanf("%d", &n); 65 for (int i = 1; i <= n; i++) 66 { 67 scanf("%d %d\n", &x[i], &y[i]); 68 } 69 70 qsort(x, y, 1, n); 71 72 Merge_Sort(1, n); 73 74 printf("%ld\n", ans); 75 76 return 0; 77 }
要注意题目中的提示部分,用 int 类型可能不足以容纳结果数字。对 x 的排序使用的是快排(快速排序)。
此程序可以通过 Tsinghua OJ 上 95%的数据,也就是 n > 1 * 10^6 的那个点无法通过(即使改了代码中的 L 也不行,Runtime error (exitcode: 11)),暂无解。