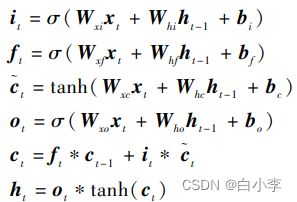2023/5/7周报
目录
摘要
论文阅读
1、标题和现存问题
2、循环神经网络和传统 LSTM
3、堆叠 LSTM和论文模型结构
4、实验准备
5、结果分析
深度学习
1、TGCN
2、公式
3、伪代码
总结
摘要
本周在论文阅读上,阅读了一篇基于注意力机制的堆叠LSTM心电预测算法的论文。模型结构采用两个LSTM网络结构,构成一种堆叠的循环神经网络模型。输出的信号再通过注意力机制,加强重点关注区域后经由全连接层输出结果。经验证,模型效果十分优越。在深度学习上,对TGCN进了学习,TGCN作为时空图卷积网络,对于处理时间和空间数据有着独特的优势。
This week,in terms of thesis reading,perusaling a paper on the stacked LSTM electrocardiogram prediction algorithm based on attention mechanism.The model structure adopts two LSTM network structures to form a stacked recurrent neural network model.The output signal is then output through the attention mechanism, strengthening the key focus area, and then outputting the results through the fully connected layer.After verification, the model has shown excellent performance.In deep learning,studying theTGCN.As a spatiotemporal graph convolutional network, TGCN has unique advantages in processing temporal and spatial data.
论文阅读
1、标题和现存问题
标题:基于注意力机制的堆叠LSTM心电预测算法
现存问题:针对日趋增长的心电数据分析需求,国内的研究大多停留在分类处理阶段,对心电异常的预测相对较少。 而心电异常的提前预警对预防接下来可能出现的危险极为重要,因此,提出了一种新的心电预测算法。
2、循环神经网络和传统 LSTM
下图为循环神经网络的典型结构,当前时刻的状态不仅取决于此刻的输入,同时与上一时刻的状态相关。 与基础神经网络不同的是,循环神经网络除了在不同层之间建立了权连接,同时在相同层之间的神经元也建立了权连接。
然而,循环神经网络在处理超长序列时,也存在一定的局限性,由于在反向传播期间,向后遍历层时梯度值衰减会导致信息随时间而丢失,因此网络会面临“梯度消失”和“梯度爆炸”的问题。 为了解决这两个问题,提出了长短期记忆网络。
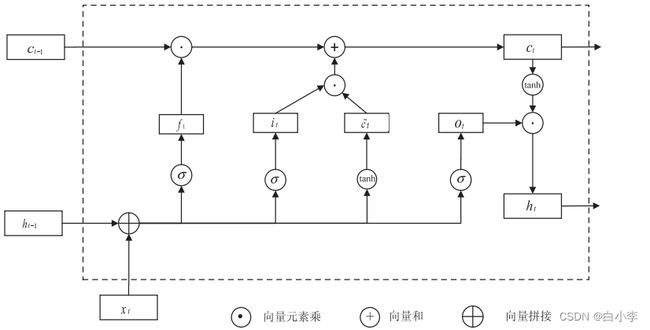
传统的 LSTM 网络具有三层:输入层、隐藏层(即LSTM 层)和输出层。 LSTM 层的关键单元是它的内存块。 每个内存块都有多个单元,它们之间有循环连接。 传统的 LSTM 具有三个乘法门:输入门、遗忘门和输出门,它们本质上是自适应的。 输入门用于学习,识别哪些信息要存储在内存中,遗忘门用于了解信息存储多长时间,而输出门用于了解存储的信息何时可以使用。
LSTM 网络通过以下公式来计算网络单元激活从输入序列x到输出序列h的映射迭代:
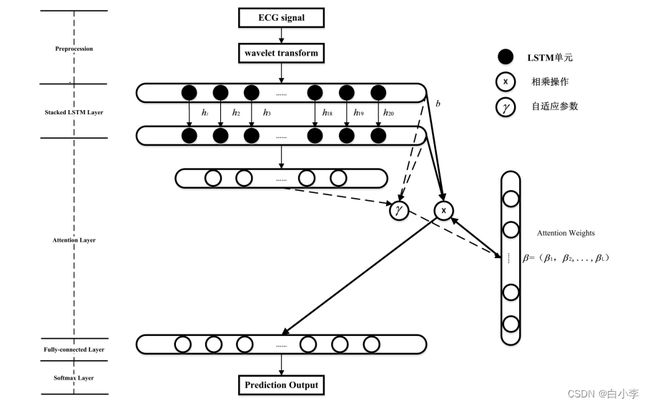
3、堆叠 LSTM和论文模型结构
堆叠 LSTM 结构可以定义为由多个 LSTM 层组成的 LSTM 模型。 上层的 LSTM 结构输出一个序列而不是单一的值到下一个 LSTM 结构,这样做的目的是加深网络,从而预测更加复杂的问题。 每个循环层可以及时展开到等效的前馈网络,其层共享相同的参数。 堆叠循环层允许在不同的时间尺度上处理这些序列,并产生更丰富的时间特征集。
神经网络中的注意力机制,也称为神经/ 人工注意力,因为它是以端到端的目标导向方式学习的,所以被视为一种自上而下的注意力。 注意力机制对模型中各类不同的元素赋予了各自不同的权重,对于重要的影响参数,对其权重进行增加;而对于不相关的信息,将其权重进行缩减。 由此,利于克服神经网络随着输入长度增加而性能下降及输入顺序不合理而计算效率低下的问题。因此,文章提出了了 Attention -LSTM的模型,结合堆叠 LSTM 结构和注意力机制,挖掘数据间的潜在规律,从而进一步提升 ECG 信号异常预测的精度。
网络在输入层有一个输入节点,并在输出层对接下来 20 个时间步长的序列进行预测。 该文在隐藏层使用 LSTM 单元,内部节点循环全连接到后续隐藏层,最后一层隐藏层与输出层全连接,使用 Softmax 激活函数来获得最终的输出:
4、实验准备
数据集:MIT-BIH 心律失常数据库
将数据集划分为两组:选取其中的 70% 作为训练集,30% 作为测试集。 训练基于堆叠 LSTM 的循环网络。 使用最大似然估计将预测误差向量拟合到多元高斯,然后使用经过训练的 LSTM 网络对测试集进行预测,并记录所得误差向量 的概率:
通过计算数据集中不同心电类别的概率分布以及总体的准确率来综合评价模型的性能,概率分布的计算方式如下所示:
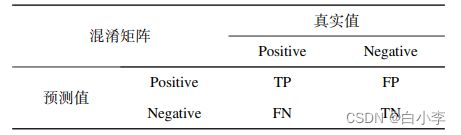
TP、TN、FP、FN 对应关系:
训练时初始学习率设置为 0. 001, Batch - size 设 置 为 300, Epochs 设 置 为500,为了防止过拟合,迭代次数设置为 10000。
5、结果分析
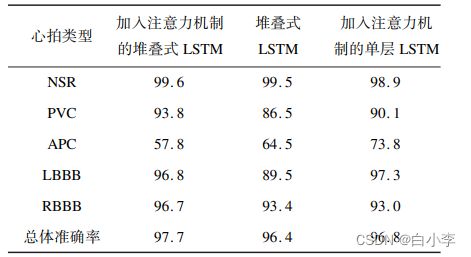
为了验证提出的堆叠式 Attention-LSTM 网络的优势,采用不同的算法在本数据集上进行对比,通过与仅使用堆叠式 LSTM 的网络模型和仅加入注意力机制的单层 LSTM 网络模型进行对比,
文中模型在性能上优于堆叠式 LSTM 模型和单层加入注意力机制的 LSTM模型。 与仅使用堆叠 LSTM 的网络模型相比,文中模型的准确率提升了 1. 3% ;与仅加入注意力机制的单层LSTM网络模型相比, 文中模型的准确率提升了0.9% ,这充分验证了文中算法的可行性和优越性。
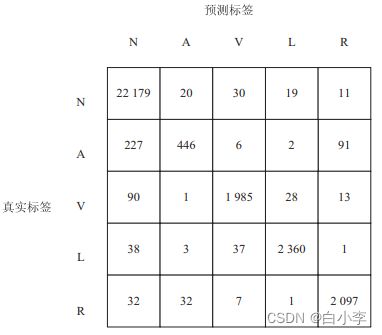
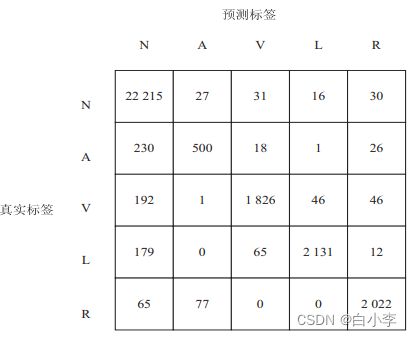
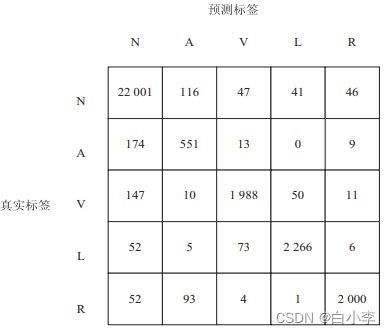
在准确率指标的基础上,同时引入了混淆矩阵对模型性能进行进一步评估
加入注意力机制的堆叠LSTM的混淆矩阵:
堆叠LSTM的混淆矩阵:
加入注意力机制的单层LSTM的混淆矩阵:
从图所示的混淆矩阵的第一列可以看出,绝大多数标签为正常窦性心律的数据均得到了正确的预测,这表明文中模型对于正常窦性心律数据的特征学习的效果较好;第二列中房性早搏的预测准确率普遍不太理想,这是由于样本标签的数量相对不足,这就对LSTM网络造成了一定的干扰,迫使模型做出了错误的预测。 而其余各列的准确率基本达到了 90% 以上,加入注意力机制的堆叠 LSTM 网络的准确率甚至达到了 96% 以上,这充分表明文中模型具有极大的优越性。
深度学习
1、TGCN
TGCN,即时空图卷积网络(Temporal Graph Convolutional Network),是一种用于处理时间序列数据的神经网络模型,它结合了图卷积网络和时间序列分析的思想,可以对时间序列数据进行有效的建模和预测。
TGCN的特点如下:
-
能够处理时间序列数据:TGCN针对时间序列数据的特点进行设计,可以对时间序列数据进行建模和预测。与传统的时间序列模型相比,TGCN具有更好的表现力和预测性能。
-
能够处理图结构数据:TGCN是基于图卷积网络的,可以处理带有图结构的数据,例如社交网络、电力网络等。与传统的基于向量的神经网络模型相比,TGCN可以利用图结构中的拓扑信息和关系信息,获得更好的表现力和泛化能力。
-
能够处理时空数据:TGCN可以处理时空数据,例如交通流量、气象数据等。TGCN将时空数据表示为图结构,利用时间维度和空间维度上的信息进行建模和预测,可以更准确地反映时空数据的特点。
-
能够处理大规模数据:TGCN采用了一些加速技巧,例如分层采样、空间变换等,可以有效地处理大规模的数据。
TGCN中的主要操作是图卷积(graph convolution)和时间卷积(time convolution)。图卷积可以看作是对邻居节点的聚合操作,用于提取节点的局部特征。时间卷积则用于提取时间序列中的局部特征。在TGCN中,这两种卷积操作是交替进行的,以捕捉时间序列数据中的时空特征。
TGCN模型首先将时间序列数据转化为时空图数据。每个时间点对应图中的一个节点,相邻时间点之间的关系则对应图中的边。接着,TGCN模型通过交替进行图卷积和时间卷积操作,来逐步提取时空图数据中的特征。最终,TGCN模型将提取的特征输入到全连接层中进行分类或回归等任务。
2、公式
其中,h{v, t}^{(l)}表示节点 v在时间步t,第l层的特征表示,sigma为激活函数,{N}v 为节点 v$的邻居节点集合,K为 Chebyshev 多项式的阶数,lambda_k 为第 k 阶 Chebyshev 多项式的特征{\Theta}k^{(l)}为第 l层与第k阶 Chebyshev 多项式的系数矩阵,{Phi}t^{(l)}表示第l层的时间权重矩阵,用于学习节点特征在时间维度上的变化。
在第l层中,节点v的特征表示h{v, t}^{(l)}由两部分组成,一部分是邻居节点的信息的加权和,另一部分是节点在时间维度上的权重与其自身特征的乘积。具体来说,第一部分用 Chebyshev 多项式来进行卷积操作,第二部分通过时间权重矩阵学习节点在时间维度上的变化规律,将其与节点特征进行加权相乘。最终,将节点特征 h{v,t}^{(l+1)} 通过激活函数映射到特征空间中。
当使用TGCN进行时间序列预测时,通常会采用以下公式:
其中,{Y}{t+1}表示在 t时刻的输入和 t+1时刻的邻接矩阵,使用权重矩阵W_t和V_t进行计算,得到 t+1时刻的预测值。A是图的邻接矩阵,X{t}表示在t时刻的输入。f是一个函数,它通过将输入和邻接矩阵进行组合并进行一些计算,得出了预测值 {Y}_{t+1}。
具体来说,TGCN中的ChebConv用于执行空间卷积,W_t是一个线性层,它将时间分片t映射到一个大小为节点数的向量,V_t是另一个线性层,它将时间分片t映射到大小为节点数乘以特征维度的矩阵。通过对x、A、W_t、V_t进行组合和计算,可以得出预测值 {Y}_{t+1}。
3、伪代码
该段代码包括了ChebConv层和时间卷积层,用于对时空图上的节点特征进行卷积。
-
将输入的节点特征x变形为(batch_size, num_nodes, num_features)的三维张量,其中batch_size表示批次大小,num_nodes表示节点数,num_features表示每个节点的特征数。
-
将边的索引和权重分别变形为(batch_size, num_nodes, num_nodes)的三维张量。
-
将时间切片time_slice变形为(batch_size, num_nodes, 1)的三维张量。
-
对时间切片进行线性变换,使用sigmoid函数将结果限制在0-1之间,将线性变换结果Wt与节点特征进行逐元素相乘,得到新的节点特征。
-
对新的节点特征x进行ChebConv层的卷积操作,得到新的节点特征。
-
对新的节点特征x进行时间卷积操作,使用线性变换Vt对节点特征进行逐元素相乘,得到新的节点特征。
-
将新的节点特征变形为(batch_size, num_nodes * num_features)的二维张量,作为输出
import torch
import torch.nn.functional as F
from torch_geometric.nn import ChebConv
class TGCNConv(torch.nn.Module):
def __init__(self, in_channels, out_channels, num_nodes, K):
super(TGCNConv, self).__init__()
self.conv = ChebConv(in_channels, out_channels, K)
self.num_nodes = num_nodes
# Add temporal convolution
self.Wt = torch.nn.Linear(num_nodes, num_nodes)
self.Vt = torch.nn.Linear(num_nodes, num_nodes)
def forward(self, x, edge_index, edge_weight, time_slice):
# Get graph topology
x = x.view(-1, self.num_nodes, x.size(1))
edge_index = edge_index.view(-1, self.num_nodes, self.num_nodes)
edge_weight = edge_weight.view(-1, self.num_nodes, self.num_nodes)
# Get time topology
time_slice = time_slice.view(-1, self.num_nodes, 1)
batch_size = time_slice.size(0)
# Get temporal convolutions
Wt = torch.sigmoid(self.Wt(time_slice))
Vt = self.Vt(time_slice)
# Compute graph convolutions
x = self.conv(x, edge_index, edge_weight)
# Compute temporal convolutions
x = torch.bmm(Wt * x, Vt.permute(0, 2, 1))
return x.view(batch_size, -1, x.size(2))总结
本周在论文阅读上面,查找了一遍时序模型的文章展开了阅读,下周计划对TGCN的论文进行学习和阅读,并对论文的代码看能不能成功跑起来。