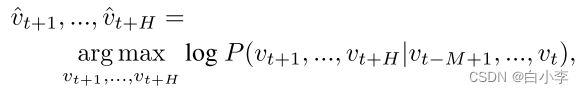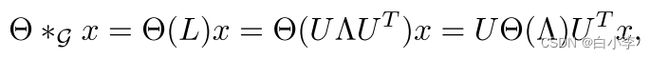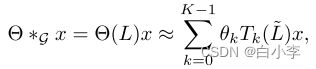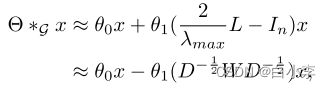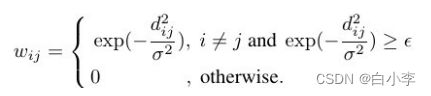2023/5/14周报

目录

摘要

论文阅读

1、标题和现存问题

2、准备知识

3、模型结构

4、实验准备

5、实验结果

深度学习

1、大气数据和水质数据

2、数据清洗

3、项目框架设定

总结

---

摘要

本周在论文阅读上，阅读了一篇时空图卷积网络:交通预测的深度学习框架的论文。文章的时空图卷积网络没有应用规则的卷积和递归单位，而是在图上公式化了问题，并建立了具有完整卷积结构的模型，从而可以以更少的参数更快的训练速度，实验结果表明模型十分优秀。在深度学习上，对于大气和水质数据的特点进行了学习，并复习了数据清洗的一些方法，最后是一些对于新模型的想法。

This week,in terms of thesis reading,perusaling a paper on spatiotemporal graph convolutional networks: a deep learning framework for traffic prediction.The spatiotemporal graph convolutional network in the article does not apply regular convolution and recursive units, but formulates the problem on the graph and establishes a model with a complete convolutional structure, which can train faster with fewer parameters.The experimental results indicate that the model is very excellent.In deep learning, studying the characteristics of atmospheric and water quality data, reviewed some methods of data cleaning, and finally, some ideas for new models.

论文阅读

1、标题和现存问题

标题：时空图卷积网络:交通预测的深度学习框架

现存问题：以往对中长期流量预测的研究大致可以分为两大类:动态建模和数据驱动方法。动态建模为了达到稳态，仿真过程不仅需要复杂的系统编程，而且需要消耗大量的计算能力，模型的假设不实际和模型的简化也降低了预测的精度。经典的统计模型和机器学习模型是数据驱动方法的两个主要代表。这些方法对高度非线性的交通流具有约束可表示性。常规模型只能处理网格结构(如图像、视频)，而不能处理一般的域。同时，用于序列学习的递归网络需要迭代训练，这就引入了误差的逐步积累。

2、准备知识

交通预测是一个典型的时间序列预测问题，预测下一个H个时间步中最可能的交通度量值(如速度或交通流量)为:

 

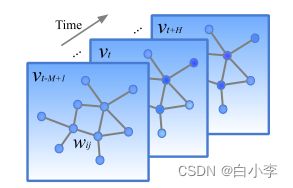
在一个图上定义交通网络，并重点研究结构化的交通时间序列，每个 vt 表示时间步长为 t 的当前交通状态帧，以图结构数据矩阵的形式记录。

 

文章基于谱图卷积的概念引入了图卷积算子“∗G”的概念，即信号x∈Rn与核的乘积Θ：

 

3、模型结构

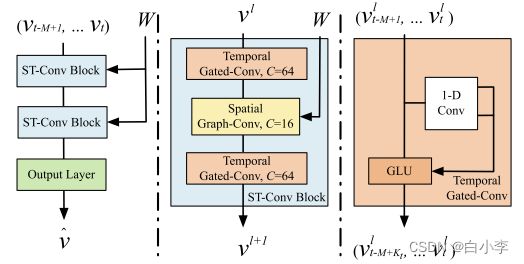
STGCN由多个时空卷积块组成，每个卷积块形成一个“三明治”结构，中间有两个门控序列卷积层和一个空间图卷积层。

 

框架 STGCN由两个时空卷积块(ST-Conv块)和一个全连接的输出层组成。每个 ST-Conv 块包含两个时间门控卷积层和中间的一个空间图卷积层。在每个块内部采用剩余连接和瓶颈策略。

图的卷积可以写为：

 

构造一个更深层的结构来恢复深度的空间信息，而不受限于由多项式给出的显式参数化。由于神经网络的缩放和归一化，我们可以进一步假设λmax≈2。因此，上式可以改写为：

 

垂直应用具有一阶近似的图卷积堆栈，可以实现与水平方向上的k本地化卷积类似的效果，所有这些都利用了中心节点的(K−1)阶邻域的信息。在这种情况下，K是一个模型中连续的过滤操作或卷积层数。此外，分层线性结构是参数经济和高效的大规模图，因为近似的阶数限制在1。

文章在时间轴上采用整个卷积结构来捕捉交通流的时间动态行为。这种特殊的设计允许并行和可控的训练过程通过多层卷积结构形成的层次表示。时间卷积层包含一个一维的因果卷积，它带有一个宽度为kt的核，后面是一个非线性的门控线性单元(GLU)。对于图G中的每个节点，时间卷积在没有填充的情况下探索输入元素的Kt邻居，这导致序列的长度每次缩短Kt-1。因此，每个节点的时间卷积输入可以看作是一个长度为m的序列，时间门控卷积可以定义为:

 

为了融合时空特征，构造时空卷积块(ST-Conv块)，对图结构时间序列进行联合处理。区块本身可以根据特定情况的规模和复杂性进行堆叠或扩展。模型中间的空间层是连接两个时间层的桥梁，时间层通过时间卷积实现从图卷积到空间状态的快速传播。“三明治”结构也有助于网络充分应用瓶颈策略，通过图卷积层对信道C进行降尺度和升尺度，实现尺度压缩和特征压缩。在每个ST-Conv块内采用层归一化，防止过拟合。对于block的输入输出：

 

STGCN用于流量预测的损失函数为:

模型STGCN的主要特征总结如下:

•STGCN是一种处理结构化时间序列的通用框架。它不仅可以解决交通网络建模和预测问题，而且可以应用于更一般的时空序列学习任务。

•时空块结合了图形卷积和门控时间卷积，可以提取最有用的空间特征，并连贯地捕获最本质的时间特征。

•该模型完全由卷积结构组成，因此以更少的参数和更快的训练速度实现了对输入的并行化。更重要的是，这种经济架构允许模型以更高的效率处理大规模网络

4、实验准备

数据集： BJER4 是用双环探测器从北京市东四环主要区域采集的。

PeMSD7 是由部署在加利福尼亚州高速公路系统主要城市地区的39000 多个传感器站实时收集到的。

两个数据集的标准时间间隔设置为 5 分钟。因此，道路图的每个节点每天包含 288 个数据点。数据清理后，用线性插值方法补全缺失值。另外，采用Z-Score方法对数据输入进行标准化处理。在BJER4 中，利用传感器站部署图构建了北京东四环线路系统的路网拓扑。通过对每条道路的隶属关系、方向和出发地点的整理， 环线系统可以数字化为有向图。

在PeMSD7 中，道路图的邻接矩阵是根据交通网络中车站之间的距离计算的。加权邻接矩阵W可以表示为:

  

为了消除非典型交通，实验仅采用工作日的交通数据。。所有的测试都使用 60 分钟作为历史时间窗口，也就是 12 个观测数据点(M = 12)来预测未来15、30和45分钟(H = 3、6、9)的交通状况。

评估指标和基线测量和评估不同方法的性能，平均绝对误差(MAE)，平均绝对百分比误差(MAPE)，和均方根误差(RMSE)。

5、实验结果

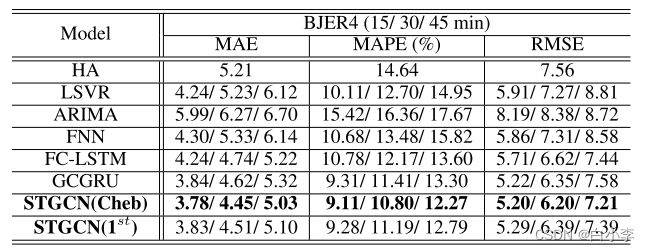
不同方法在数据集BJER4上的性能比较：

 

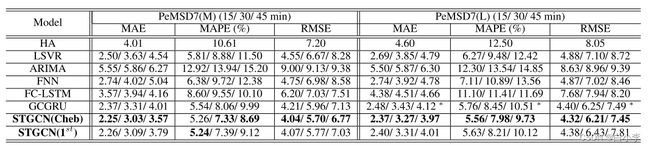
不同方法在数据集PeMSD7上的性能比较：

 

文章所提出的模型在三个评价指标中均取得了最佳的性能，且具有统计学意义(双尾t检验，α = 0.01, P < 0.01)。我们可以很容易地观察到，传统的统计和机器学习方法可能在短期预测方面表现良好，但由于错误积累、记忆问题和空间信息的缺乏，它们的长期预测并不准确。由于ARIMA模型不能处理复杂的时空数据，其性能最差。深度学习方法通常比传统的机器学习模型获得更好的预测结果。STGCN在数据集PeMSD7上的优势比BJER4更明显，因为PeMS的传感器网络更加复杂和结构化，模型可以有效地利用空间结构进行更准确的预测。

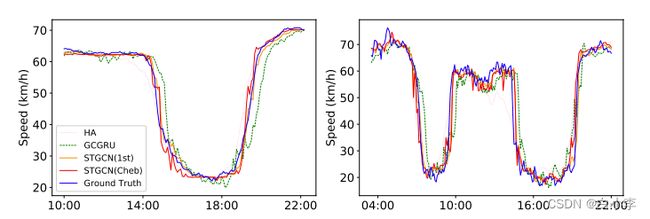
比较基于图卷积的三种方法 :GCGRU、 STGCN(Cheb) 和STGCN(1st)在早高峰和晚高峰时间的预测。

 

文章的STGCN方案比其他方法更准确地捕捉了交通高峰期的趋势;而且它能比其他车辆更早地检测到交通高峰期的结束。由于有效的图卷积和堆叠时间卷积结构，我们的模型能够快速响应交通网络的动态变化，而不像大多数循环网络那样过度依赖历史平均。

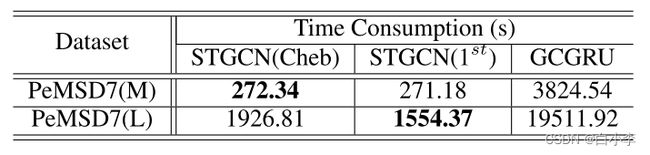
在我们的方案中，可以看到沿时间轴的卷积的好处：

 

STGCN采用默认设置。文章模型STGCN只消耗272秒，而rnn型的模型GCGRU在PeMSD7(M)上消耗3824秒。这种训练速度的14倍加速主要得益于应用时间卷积而不是循环结构。由于一阶逼近不局限于多项式的参数化，模型的优点也逐渐显现出来。与STGCN(Cheb)相比，模型STGCN(1)在更大的数据集上加速约20%，性能十分优秀。

深度学习

1、大气数据和水质数据

大气数据和水质数据是时序型数据中十分常见的两种，二者随着时间的变化而变化，因此是属于需要长期监测和分析的数据类型。

水质数据的组成和特点：

1. 组成：水质数据包括水中各种化学物质的浓度、pH值、温度等参数。

2. 特点：水质数据通常具有周期性和季节性变化，受天气、地理位置、人类活动等因素的影响较大。常见的水质指标包括溶解氧、浑浊度、氨氮、总磷等，用于评估水体的健康状况和适宜用途。

空气数据的组成和特点：

1. 组成：空气数据包括大气中的气体浓度、颗粒物浓度、温度、湿度等参数。

2. 特点：空气数据受气象条件、地理位置、人类活动和污染源等因素的影响。常见的空气指标包括二氧化碳浓度、臭氧浓度、PM2.5和PM10颗粒物浓度等，用于评估空气质量和环境污染程度。

2、数据清洗

由于环境问题或者其它问题导致监测的数据是缺省或者错误的，此时就应当对数据进行清洗：

1. 缺失值处理：检查数据中是否存在缺失值，并根据情况选择合适的方法来处理。可以使用插值方法填充缺失值，如线性插值或基于邻近值的插值。

2. 异常值处理：识别和处理异常值，这些异常值可能是由于数据采集或传感器故障引起的。可以使用统计方法，如均值加减几倍标准差的阈值判断法，来识别和处理异常值。

3. 平滑处理：平滑处理可以降低噪声对数据的影响，使趋势更加清晰。常见的平滑方法包括移动平均、加权移动平均和指数平滑。

4. 数据去重：检查数据是否存在重复记录，并将其删除或合并，确保每个时间点只有唯一的数据值。

5. 时间对齐：对于多个数据源或传感器，确保时间戳的一致性和对齐，以便后续分析和比较。

6. 数据格式转换：根据需要，将数据转换为适合分析和建模的格式，如将日期时间列转换为时间戳或统一的日期时间格式。

7. 数据规范化：对不同量纲的数据进行归一化或标准化，以便进行综合分析或建模。

8. 数据验证：验证清洗后的数据是否符合预期的范围和规则，确保数据的准确性和可靠性。

以基于邻近值的插值法来进行代码实例演示

import pandas as pd
import numpy as np
​
# 创建示例数据
data = pd.DataFrame({
    'timestamp': pd.date_range('2023-01-01', periods=10, freq='D'),
    'value': [5, 8, np.nan, 12, np.nan, 10, 15, 18, np.nan, 20]
})
​
# 使用基于邻近值的插值法进行数据清洗
data['value'] = data['value'].interpolate(method='nearest')
​
# 打印清洗后的数据
print(data)

清洗前后的数据：

 

缺失值被用最近的非缺失值进行了插值处理。在这个示例中，第2行的缺失值被插值为8，第4行和第5行的缺失值被插值为10，第8行的缺失值被插值为19。

3、项目框架设定

项目计划采用GCN+LSTM（GRU）模型搭建时序卷积图神经网络框架。计划以下步骤：

1. 数据准备：将时序数据转化为图结构的表示形式。每个站点可以看作图中的一个节点，站点相邻之间可以建立边连接。同时，每个节点包含对应的数据特征。

2. 图卷积网络（Graph Convolutional Network，GCN）：使用GCN来对时序数据进行图卷积操作，以捕捉节点间的时序关系。GCN可以在节点特征上聚合邻居节点的信息，并更新节点的特征表示。

3. LSTM层：在每个节点上应用LSTM层，以建模时序依赖关系。LSTM可以有效地处理序列数据，并捕捉长期依赖关系。

4. 输出层：根据具体任务需求，可以添加相应的输出层，例如全连接层、Softmax层或线性层，用于进行分类、回归或其他预测任务。

5. 模型训练：使用适当的损失函数（如交叉熵损失函数、均方误差损失函数等）和优化算法（如Adam、SGD等），对模型进行训练。通过最小化损失函数，优化模型参数，使模型能够更好地拟合时序数据。

6. 模型评估：使用测试集或交叉验证方法对训练好的模型进行评估，计算相应的指标（如准确率、均方误差等），评估模型在时序数据上的性能。

创新点设想：

1. 在GCN模型中，对于输入数据，加入当地的社会经济发展因素，将其作为参数进行输入，对于水质以及大气的规律增强说服力。

2. 和其他模型不同，本次设想的模型为由点到面的变化，不关考虑了单个节点，也将各个节点之间的联系也给考虑了进去。

3. 在模型实现以及测试中，可以对重要影响部分加入注意力机制，提升其重要性，排除非必要因素的影响。

总结

本周对于TGCN模型的相关论文进行了学习，GNN和时序模型相结合的新模型，对于处理面的时序型数据是有着优异的效果，最后对于新模型提出了一些自己的看法，由于本周事情比较多就没有再进行深入的学习，等下周考完最后一次试后再继续这方面的学习。