2023年天府杯数学建模竞赛A 题:震源属性识别模型构建与震级预测-详细解题思路代码与答案
问题 1:针对附件 1~8 中的地震波数据,找出一系列合适的指标与判据,构建震源属性识别模型,进行天然地震事件(附件 1~7)与非天然地震事件(附件 8)的准确区分;
思路:首先需要进行数据预处理,将各组波形数据进行整理,并对应打上天然地震事件0和非天然地震事件1的标签。接着对应每组波形数据,进行特征构建与提取,如峰度、偏度、振幅、均值、标准差、最小最大值,然后可以进行适当的特征筛选(如卡方检验或者相关系数判别法),由此建立出二分类机器学习模型(可以使用支持向量机、逻辑回归、随机森林等等分类模型,也可以使用异常检测算法如LOF/LOCI/ABOD算法,可以更好地处理正异常样本不均衡的情况)。
#数据处理
import pandas as pd
import numpy as np
df_feature=pd.DataFrame([],columns=['事件','观测站','均值','振幅','标准差','最小值','最大值','峰度','偏度','是否天然'])
def get_features(path,event,station):#针对天然事件1~7
fr = open(path, 'r')
all_lines = fr.readlines()
dataset = []
for line in all_lines:
line = line.strip().split(' ')
dataset.append(line)
# 转换成dataframe
df = pd.DataFrame(dataset).T
df[0] = pd.to_numeric(df[0], errors='coerce')
range=df[0].max()-df[0].min()
biaoqian=0 #附件1-7
features_list=[event,station,df[0].mean(),range,df[0].std(),df[0].min(),
df[0].max(),df[0].kurt(),df[0].skew(),biaoqian]
return features_list
def get_features_8(path,event,station):#针对非天然事件8
fr = open(path, 'r')
all_lines = fr.readlines()
dataset = []
for line in all_lines:
line = line.strip().split('\n')
dataset.append(line)
# 转换成dataframe
df = pd.DataFrame(dataset)
df[0] = pd.to_numeric(df[0], errors='coerce')
range=df[0].max()-df[0].min()
biaoqian=1 #附件8
features_list=[event,station,df[0].mean(),range,df[0].std(),df[0].min(),
df[0].max(),df[0].kurt(),df[0].skew(),biaoqian]
return features_list
for i in range(1,8):
for j in range(1,21):
path = 'A/附件'+str(i)+'/'+str(j)+'.txt'
df_feature.loc[len(df_feature),:]=get_features(path,i,j)
for i in range(8,9):
for j in range(1,31):
path = 'A/附件'+str(i)+'/'+str(j)+'.txt'
df_feature.loc[len(df_feature),:]=get_features_8(path,i,j)
print(df_feature)
df_feature.to_csv('特征构建.csv',index=False)问题 2:地震波的振幅大小、波形特性与震级有着显著关联。根据已知震级大小的附件 1~7 中数据(震级大小分别为:4.2、5.0、6.0、6.4、7.0、7.4、8.0),恰当地挑选事件与样本,建立震级预测模型, 尝试给出附件 9 中地震事件的准确震级(精确到小数点后一位)。
思路:这里可以同样选取前一问中提到的特征,将标签修改为对应的震级。针对每个附件利用箱线图进行异常值的剔除,然后使用剩下的样本和震级标签构建预测模型,这里可以采用决策树、支持向量机回归等方法。
箱线图
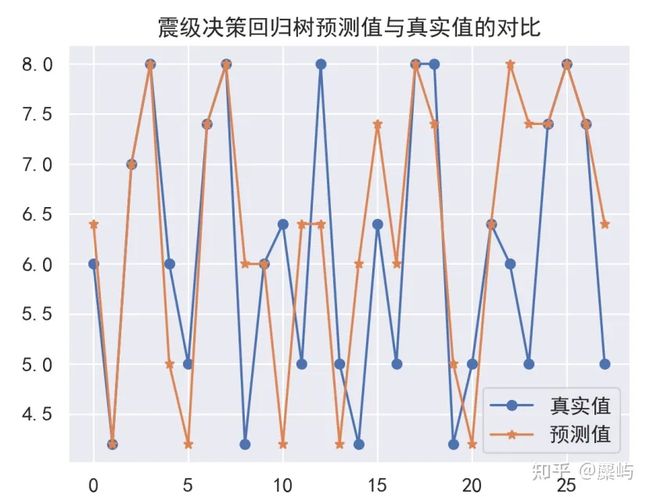
决策树预测
问题 3:库深、库容、断层类型、构造活动/基本烈度、岩性等是影响水库诱发地震震级大小的重要因素。请根据附件 10 中 102 个 水库地震样本,尝试建立水库基本属性资料与震级的关系模型,并给出合理的依据。
思路:首先观察给出的数据,发现其中含有较多的字符型变量,需要转换成数值变量,可以采用直接转化或者采用独热编码的方式。首先可以使用相关性热力图来简单判断各个特征与震级的相关性联系,然后将震级视为标签,采用决策树(更具可解释性)的方法构建各特征与震级的具体关系。
预测结果
模型评价