树状数组学习总结

今天本初中生蒟蒻学习了一下$树状数组$，总结一下~~~

树状数组的实现

功能简介

• 快速求前缀和（$O(lo{g}_{2}n)$）
• 修改某一个数（$O(lo{g}_{2}n)$）

---

树状数组图示

树状数组其实就是如图所建立的~~~

---

下面引入一个函数——lowbit

lowbit(x)是x的二进制表达式中最低位的1所对应的值。

例如：

1. $lowbit(6)$
   6的二进制为$(110{)}_2$，$lowbit(6)=(10{)}_2=2$
2. $lowbit(8)$
   8的二进制为$(1000{)}_2$，$lowbit(8)=(1000{)}_2=8$

$代码$

int lowbit(int x)
{
    return x & -x;
}

---

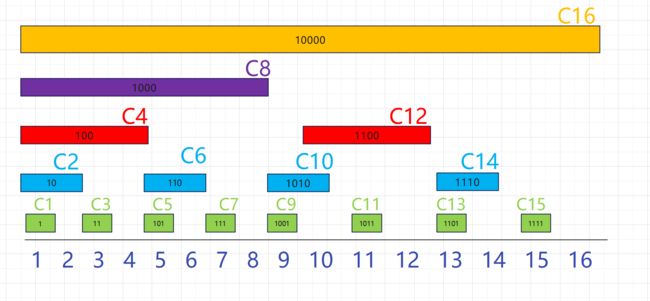
知道这个函数之后，我们再来看这张图~~~
对于第一行的数字，$lowbit之后都等于(1{)}_2$
对于第二行的数字，$lowbit之后都等于(10{)}_2$
对于第三行的数字，$lowbit之后都等于(100{)}_2$
$\dots$

这就是这张图的神秘之处~~~

---

快速求前缀和

我们再来观察这张图

如果我们想求$C_8$
那么$C8=A_8+C_7+C_6+C_4$
然后我们看一下这3个数7,6,4
$7-lowbit(7)(1)=6$
$6-lowbit(6)(10)=4$

综上所述:
$C_x=C_{x-lowbit(x)}+C_{x-lowbit(x)-lowbit(x-lowbit(x))+\cdots +A_x}$

$代码$

int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i]; //tr为我们的树状数组

    return res;
}

---

修改某一个数

还是这张图~~~

假如我们要修改的是C1，让他加上10
那么我们看一下他需要更新的点：$C_1,C_2,C_4,C_8,C_{16}$
再来看看他们的性质：
$1+lowbit(1)(1)=2$
$2+lowbit(2)(10)=4$
$4+lowbit(4)(100)=8$
$8+lowbit(8)(1000)=16$

综上所述:$对于每一个C_{x+lowbit(x)}都加上所要增加的数，注意：x每次让其等于x+lowbit(x)$

$代码点这里！$

void add(int x, int val) //val为要加上的值
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += val; //tr是树状数组
}

---

树状数组的应用

例题1——楼兰图腾

$题目描述$

在完成了分配任务之后，西部 314 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀(V)，一个部落崇拜铁锹(∧)，他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。

西部 314 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 $n$ 个点，经测量发现这 $n$ 个点的水平位置和竖直位置是两两不同的。

西部 314 认为这幅壁画所包含的信息与这 $n$ 个点的相对位置有关，因此不妨设坐标分别为 $(1,y_1),(2,y_2),\dots ,(n,y_n)$，其中 $y_1\sim y_n$ 是 $1$ 到 $n$ 的一个排列。

西部 314 打算研究这幅壁画中包含着多少个图腾。

如果三个点 ($i,y_i),(j,y_j),(k,y_k)$ 满足 $1\le i<j<k\le n$ 且 $y_i>y_j,y_j<y_k$，则称这三个点构成 V 图腾;

如果三个点 $(i,y_i),(j,y_j),(k,y_k)$ 满足 $1\le i<j<k\le n$ 且 $y_i<y_j,y_j>y_k$，则称这三个点构成 ∧ 图腾;

西部 314 想知道，这 $n$ 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 V 的个数和 ∧ 的个数。

输入格式

第一行一个数 $n$。第二行是 $n$ 个数，分别代表 $y1，y2,\dots ,yn$。

输出格式

两个数，中间用空格隔开，依次为 V 的个数和 ∧ 的个数。

数据范围

对于所有数据，$n\le 200000$，且输出答案不会超过 $int64$。
$y_1\sim y_n$ 是 $1$ 到 $n$ 的一个排列。

输入样例：

5
1 5 3 2 4

输出样例：

3 4

---

$思路$

答题思路是求出每个点左边比他高，和右边比他高的个数，相乘即使V数
再求出每个点左边比他低，和右边比他低的个数，相乘即使∧数

本题可以用树状数组来做，我们可以把纵坐标看做树状数组的下标。

即，在这个图中$C_x$表示为x及比x低的点的个数
所以对于每次插入一个点时，我们都让当前点及往上的点都加1.
这样我们在求一个每一个点的V数时：
$个数就是(sum(n)-sum(a_i))\times (n-a[i]-sum(n)+sum(a_i))$
注：因为我们在加1的时候算上了当前点，而题目中问的是比$a_i$低的点，不包括$a_i$，所以我们这里用前缀和思想$sum(n)-sum(a_i)$，而不是$sum(n)-sum(a_i-1)$
我们在求一个每一个点的∧数时：
$个数就是sum(a_i-1)\times (a[i]-1-sum(a_i-1))$
注：这里减1是因为如果是$sum(a_i)$就会算上$a_i$这个点，减1就不会了

---

$代码$

#include 
#include 
#include 
#define int long long

using namespace std;

const int N = 2e5 + 10;

int n;
int a[N];
int high[N], low[N];
int tr[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int val)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += val;
}

int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];

    return res;
}

signed main()
{
    cin >> n;
    
    for (int i = 1; i <= n; i ++)
        cin >> a[i];
    
    int r1 = 0, r2 = 0;
    for (int i = 1; i <= n; i ++ )
    {
        high[i] = sum(n) - sum(a[i]);
        low[i] = sum(a[i] - 1);
        r1 += high[i] * (n - a[i] - high[i]);
        r2 += low[i] * (a[i] - 1 - low[i]);
        add(a[i], 1);
    }
    
    cout << r1 << " " << r2 << endl;
}