隐马尔科夫模型
隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model, HMM)可以由观测序列推断出概率最大的状态序列.
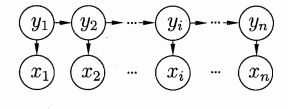
HMM中的变量可分为两组:
状态变量(隐变量): { y 1 , y 2 , . . . , y n } \left \{ y_{1},y_{2},...,y_{n}\right \} {y1,y2,...,yn};序列标注问题中的标注.
观察变量: { x 1 , x 2 , . . . , x n } \left \{ x_{1},x_{2},...,x_{n}\right \} {x1,x2,...,xn};序列标注问题的文本序列.
1、两个基本假设
隐马尔可夫模型做了两个基本假设:
(1)齐次马尔可夫性假设
(2)观测独立性假设
关于齐次马尔可夫假设: 上图中的箭头表示了变量间的依赖关系.因为齐次马尔可夫假设,t时刻的状态 y t y_{t} yt仅依赖于t-1时刻的状态 y t − 1 y_{t-1} yt−1,与其余n-2个状态无关。
关于观测独立性: 上图中的箭头表示了变量间的依赖关系.因为观测独立假设,在任意时刻,观察变量的取值仅依赖于状态变量,即 x t x_{t} xt由 y t y_{t} yt确定,与其他状态变量及观察变量的取值无关。
2、HMM构造
隐马尔可夫模型由初始状态概率向量 π \pi π 、状态转移概率矩阵A和观测概率矩阵B决定。 π \pi π和A决定状态序列,B决定观测序列。因此,隐马尔可夫模型λ 可用三元符号表示,即λ=(A, B, π \pi π)
A,B, π \pi π 称为马尔可夫模型的三要素。
状态转移该概率矩阵A与初始状态概率向量确定了隐藏的马尔科夫链,生成不可观测的状态序列。观测概率矩阵B确定了如何从状态生成观测,与状态序列综合确定了如何产生观测序列。
隐马尔可夫模型的形式定义如下:
设 V = { v 1 , v 2 , . . . , v M } V= \left \{ v_{1},v_{2},...,v_{M}\right \} V={v1,v2,...,vM}是所有可能的观测的集合, Q = { q 1 , q 2 , . . . , q N } Q = \left \{ q_{1},q_{2},...,q_{N}\right \} Q={q1,q2,...,qN}是所有可能的状态的集合。其中,N是可能的状态数,M是可能的观测数。 X = { x 1 , x 2 , . . . , x T } X = \left \{ x_{1},x_{2},...,x_{T}\right \} X={x1,x2,...,xT}是长度为T的观测序列, Y = { y 1 , y 2 , . . . , y T } Y = \left \{ y_{1},y_{2},...,y_{T}\right \} Y={y1,y2,...,yT}是对应的状态序列。
A是状态转移概率矩阵: A = [ a i j ] N × N A = [a_{ij}]_{N\times N} A=[aij]N×N
其中, a i j = P ( y t + 1 = q j ∣ y t = q i ) a_{ij}=P(y_{t+1}=q_{j}|y_{t}=q_{i}) aij=P(yt+1=qj∣yt=qi), i=1,2,…N; j=1,2,…N
是在时刻t处于状态 q i q_{i} qi的条件下在时刻t+1转移到状态 q j q_{j} qj的概率。
B是观测概率矩阵: B = [ b j ( k ) ] N × M B = [b_{j}(k)]_{N\times M} B=[bj(k)]N×M
其中, b j ( k ) = P ( x t = v k ∣ y t = q j ) b_{j}(k)=P(x_{t}=v_{k}|y_{t}=q_{j}) bj(k)=P(xt=vk∣yt=qj), k=1,2,…M; j=1,2,…N
是在时刻t处于状态 q j q_{j} qj的条件下生成观测 v k v_{k} vk的概率。
π \pi π是初始状态概率向量: π = ( π i ) \pi=(\pi_{i}) π=(πi)
其中, π i = P ( x 1 = q i ) \pi_{i}=P(x_{1}=q_{i}) πi=P(x1=qi), i=1,2,…N; 是时刻t=1处于状态 q i q_{i} qi的概率。
3、HMM使用
概率计算问题。给定模型λ=(A, B, π \pi π)和观测序列 X = { x 1 , x 2 , . . . , x n } X = \left \{ x_{1},x_{2},...,x_{n}\right \} X={x1,x2,...,xn},计算在模型λ下观测序列X出现的概率P(X|λ)。前向-后向算法是通过递推地计算前向-后向概率可以高效地进行隐马尔可夫模型的概率计算。
学习问题。已知观测序列 X = { x 1 , x 2 , . . . , x n } X = \left \{ x_{1},x_{2},...,x_{n}\right \} X={x1,x2,...,xn},估计模型参数λ=(A, B, π \pi π),使得在该模型下观测序列概率P(X|λ)最大。即用极大似然估计的方法估计参数。Baum-Welch算法,也就是EM算法可以高效地对隐马尔可夫模型进行训练。它是一种非监督学习算法。
预测问题。已知模型λ=(A, B, π \pi π)和观测序列 X = { x 1 , x 2 , . . . , x n } X = \left \{ x_{1},x_{2},...,x_{n}\right \} X={x1,x2,...,xn},求对给定观测序列条件概率P(Y |X)最大的状态序列 Y = { y 1 , y 2 , . . . , y n } Y = \left \{ y_{1},y_{2},...,y_{n}\right \} Y={y1,y2,...,yn}。维特比算法应用动态规划高效地求解最有路径,即概率最大的状态序列。
Reference
1.《统计学习方法》,李航著
2.《机器学习》,周志华著