光学仿真2020-12-09

光学仿真三千问（讲人话）

（第二篇———光学(第一小节)）

上帝说要有光，光从何来？

lights ，对于它的讨论推动了物理学两次飞跃， relativity and quantum !
大家可能发现了，我这个人喜欢追根溯源，我要落地的程序是1，而我必须从100开始讲起！
没错！
让我们走进相对论和量子力学1，从而认识光的本质！然后对他在摄像机中的过程分析，from 0 to 100;

人类对于光的本质的认识

一，光的认知：

光的认知过程可简单划分为两个阶段，17世纪以前的直观体验阶段和17世纪以后的科学认知阶段。

17世纪光学在欧洲诞生了，欧洲成为了当时光学研究的前沿阵地。几何光学和波动光学，从数学和科学的角度描述了光。几何光学阐述了光的直线传播、反射、折射等，波动光学阐述了光是一种电磁波，光学研究进入了科学认知的历程。科学认知即光的科学，需要了解光的本性是什么、光是怎么产生的、怎么传播的，以及与物质的相互作用，甚至通过物质的相互作用怎么去调控光，这些也正是光科学研究主要内容。

几何光学是光学发展史上的转折点，在这个时期建立了光的反射定律和折射定律，奠定了几何光学的基础。其中最重要的是光的折射定律，折射率决定了光的传播和光的相互作用，是光学研究中最基本的数值，介电常数与极化率等都是与折射率紧密关联的常数。这便是微粒说的天下时期；

17世纪下半叶，牛顿和惠更斯等把光的研究引向进一步发展的道路。1672年牛顿完成了著名的三棱镜色散试验，经过三棱镜的太阳光可分出五颜六色的光，这是最早的波长的概念。但是，牛顿却认为光是粒子性的。牛顿的微粒流的假设则难以解释光在绕过障碍物之后所发生的衍射现象。惠更斯反对光的微粒说，认为光是波动的。光向外传播类似于将石头掷于水中，波向外传播，每一点都是一个源，再次向外传播。这与光是粒子的，类似于打子弹，是一个粒子一个粒子的向前传播的学说相矛盾。惠更斯运用他波动理论中的次波原理，不仅成功地解释了反射和折射定律，还解释了方解石的双折射现象。这个时期也可以说是几何光学向波动光学过渡的时期，是人们对光的认识逐步深化的时期。

1801年，杨氏干涉实验证明了光的波动性。托马斯·杨把一支蜡烛放在一张开了一个小孔的纸前面，这样就形成了一个点光源。在带孔的纸后面再放一张纸，将第二张纸开出两道平行的狭缝。从小孔中射出的光穿过两道狭缝投到屏幕上，到达不同位置时位相不同，叠加后出现强度的增强或减弱，会形成一系列明、暗交替的条纹，这就是著名的双缝干涉条纹。虽然这一实验充分证明了光具有波动性，但是光的波动理论仍然不被人们认可，光的波动性一直处于争论之中。

当时欧洲科学中心，法国科学院提出了一个著名的题目—泊松亮斑，菲涅尔成功地利用这一题目证明了光的波动性。菲涅尔将屏孔的尺寸改变成与波长量级相当的大小，实验中发现屏幕上出现了干涉条纹，中间出现了亮斑，证明了光的波动性。

光的波动性被认可后，促进了电磁学的快速发展。麦克斯韦方程是现代电磁学的基础，而光的所有性质都可以用麦克斯韦方程来解释， “光也是一种电磁波”这一观点逐渐被大家认可。从无线电波到伽马射线都是电磁波，光只是其中很小的一部分，这时光的波动学说是全盛时期；

二，光所引起的两次思考：

19世纪末，经典物理的大厦已经建成。汤姆逊在新年祝词中讲到，经典物理中只剩下“两朵黑云”，其中一朵与光学紧密相关，即波动理论的困惑。用波动理论计算黑体辐射会无限大的增强—瑞利金斯曲线，与实际测量不符，即紫外灾难。为了解释这个难题，数学家普朗克从物质的分子结构中借用不连续的概念，提出了量子论。他认为光具有量子化特性，能量是一份一份的，并不是连续的，即光是粒子的，这可以很好地解释紫外灾难。

爱因斯坦提出光量子学说，用光电效应证明了光的粒子性，并获得诺贝尔物理学奖。这标志着光科学的研究进入了量子光学时期。而另一个促进量子力学诞生的重要研究是对“太阳黑线”的研究。应用光谱仪测量阳光照射的谱线中总是有几条稳定存在的谱线，起初人们无法判定黑色谱线的来源，后确定为太阳光到达地球的过程中吸收了大气中的某些元素，于是在太阳光谱中就没有这些频率的光波，形成了暗线。但吸收线为单线，为了解释此现象，波尔提出了原子构造学说，认为原子由原子核和核外电子组成，电子存在不同的能级，吸收光子后电子从下能级跃迁至上能级将光子能量吸收，由此提出了原子结构和能量不连续性，解释了太阳黑线现象，量子力学由此诞生。

我们可以看到，光学在量子力学的建立过程中做出了重要的贡献。光子概念的提出、光电效应的发现、紫外灾难的解释、光谱暗线的解释，以及能级的概念提出等，这些研究奠定了当代量子物理学的框架，而量子物理学的发展又促进了光学的巨大发展。

剩下的另一朵乌云是关于光速不变的问题，这个问题的本质是在否认光在以太为介质的连续稠密中震荡传播，迈克尔逊莫雷实验早就否认了这点，否则应该出现的干涉条纹呢？他的实验说明光速不会因为参考系的变换而变换。

也就是说以光速去追光，测量后发现，光速还是c,

我个人第一次的直觉觉得，这个我们测量的原因有关，想象一下，你去测量光，假设光是波，那么人类怎样去探测光呢？

我想假设任何速度的测量都是需要力学量（广义的）去测量的，那么他们的观测是在光耦合到探测器的发生的一个很小的时间内发生的，那么测得的量极有可能是耦合时的光速，
你可能说！不对，最早光速的探测就没有任何探测器，用的是肉眼去看齿轮缝隙的明暗变化！
你错了，眼睛不过也是一种低精度的探测器罢了，最早的光速测量方法如下：

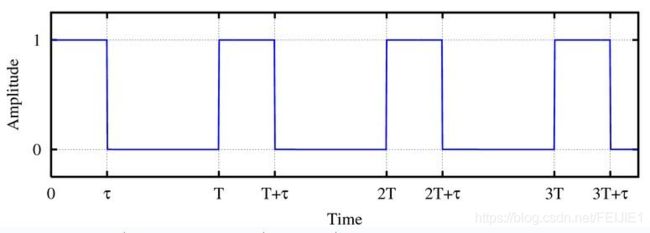
用两个齿轮数不同转速不同的齿轮在一个轴上转动（两个齿轮的距离已知），让光从左通过尺牙达到右边的屏幕上，由于延时效应的存在，光会
在右边的屏幕上周期性出现，明亮周期为T黑暗周期为t，假设第一个齿轮转速为a,齿数为na,第二个齿轮转速为b,齿数为nb, 半径都为r，每个尺牙占据固定弧长p, 两个齿轮距离为L，那么:

对于一个齿轮就是有：

$$T=(2\ast pi/n-p)/w\ast r,t=p/w\ast r;$$

明暗成了一种方波表示：
a齿轮的方波
b齿轮的方波

得知了两者的方波就可以对两个方波级联的系统相乘为新的方波，而这个方波的形状由光程决定，l这个距离会让。有一定的延时效应的存在，也就是说会延时个
$$time=l/c;$$
造成
$$time\ast (wa-wb)$$
的相位差；
（让第二个方波平移这个距离后再让两个波相乘），这样通过观察相乘后的方波周期就可以确定光速！（相位差和不同的转速（一定要不同！）会导致这个问题的周期性！）
这样测出来的光速其实已经达到了2.9kkm/s,非常精准了，这还是在没有发明电力的时代人们通过蒸汽机测得！
牛逼！
后来人们又通过迈克尔逊莫雷实验测得了光速，后来麦克斯韦又通过电磁理论预言了电磁波并严格计算出来了光速；
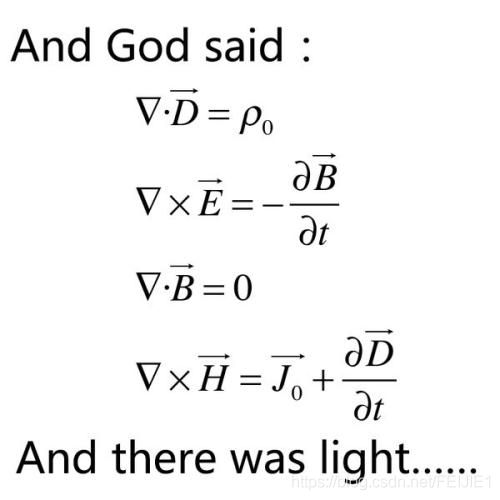
我们可以发现，通过光的直线传播（粒子说）和波动理论两个方面
都解决了光速的问题，光速的测量方法又让波粒二象性大获成功；

是这样吗？？

回顾历史，回顾今天，本人觉得，no，这个我们后面再说，避免太过硬朗，以至于大家感到厌烦！

kekeke,一不小心有又展开太多，让我们继续，刚才我们说的是探测过程，探测是在探测器耦合光某种方式（眼睛也是探测器），很可惜的是，我们目前并没有很明确的探测器跟光的耦合实际过程，进入探测器的那一瞬间，我们是如何探测这个过程的呢？noop,我们无法探测过程，我们只是让结果在模型的标准下去调整我们的理论和参数，我们能看到光还没传播到眼睛的画面吗？我知道，你不知道我想说啥，其实我也很难用语言说出来。。。
给我点时间以后我会说清这种感觉！

三：老爱的理论：
我觉得个人来说，广相在我心里的地位高于quantum,所以我们从老爱说起来！先！
所以，那你光速不变是哪里出了问题呢？

还记得我在第一章说的希尔伯特空间吗？
爱因斯坦的狭义相对论这事儿其实跟阿尔伯特关系不大，，，，，
洛伦兹老人家的四维旋转早就解决了他的一切数学基础，更本质，更优美；
咋弄！？
来： 问题的核心是参考系无论咋动，光速不变，给你两分钟，你来构造一个函数，光速永远不变：

time up …
先给出速度叠加公式（先不证明，体验最重要），v1是坐标系相对速度，v2是这个坐标物体的速度；
$$v1与v2叠加=(v1+v2)/(1+v1\ast v2/c^2);$$
这样，你试试
$$c"+"c=(c+c)/(1+c^2/c^2)=c;$$

昂，光速不变，也许你还能构造出新的方程，请留言给俺。。
来，我们来一起推导一下它，并看一下它的物理意义!
怎么去推到呢？
假设x‘是一个坐标系相对于x速度为v;则有：

$$x^{\prime }=x-v\ast t$$

这是笛卡尔变换，没什么不对！
对吧
也就是说：
真实的相对速度为v时，以上公式成立，
（我为什么说是真实速度呢？
因为我认为测量的速度并不是真实的速度！
曾在一本失传绝学上看过解释菲索实验的书，里面基本是在否认狭义相对论，里面解释狭义相对论是一种近似！并且详细解释了一些不能被解释的现象；；；；；）
ok,言归正传！
刚才说了x’相对x速度为v时候的坐标变换，
那么x相对x’时候的变换规律会变吗？！
当然不会变，仍然是
$$x=x^{\prime }-v\ast t$$
因为必须对称，两个坐标系是公平的。
那么
如果x’相对于x以v运动,就有：
$$x^{\prime }=x-v\ast t;x=x^{\prime }+v\ast t;$$
带入x’，则：
$$x=x^{\prime }+v\ast t=x-v\ast t+v\ast t=x$$

没毛病！！
说明这个理论自身严格自洽；也就是说笛卡尔在数学上是自洽的！
他在说两个平面的夹角（法线夹角）不变的情况下平移两个平面的关系！
那么就会还有平移两个平面但夹角变的情况对吧！
我们来试一下！假设旋转角度和位移成正比比例为q,（这是我独创的方法哦，，请看下去！）
那么根据投影定理：

$$x=(x’-v\ast t^{\prime })/cos(q^{\prime });q^{\prime }=-kv{t}^{\prime };$$
$$x^{\prime }=(x+v\ast t)/cos(q);q=kvt;$$

如果光速不变是正确的；
那么我们将会有：
$$x=ct;$$
$$x^{\prime }=c\ast t^{\prime }$$
那么带入后就有：
$$c\ast t=(c\ast t’-v\ast t^{\prime })/cos(q^{\prime });q^{\prime }=-kv{t}^{\prime };$$
$$c\ast t^{\prime }=(c\ast t+v\ast t)/cos(q);q=kvt;$$

这两个式子，
那么我们再把他们带入求解
那么就有：
$$cos(q)\ast cos(q^{\prime })=1-v^2/c^2;q=kvt,q^{\prime }=kv{t}^{\prime }$$

这样我们如果要相信t和t’的同时性，那么cos(q)=cos(q’)；
这样：
$$cos(kvt)=1-v^2/c^2$$
正好他小于等于一；
$$k=acos(1-v^2/c^2)/vt;$$
可以看出k随着时间而变；
以上是我对狭义相对论的解释；

上图就是狭义相对论；
（这里有一个问题，就是cos(q)为什么要等与cos(q’),我有着巨大的疑问，就这样取算术平均数到底意味着什么？
意味着时空对称；
从骨子里这样就是一个荒谬的假设，左右为什要对称？
这就造就了相对论中不可能有非对称的场，或者说之后的广相也受到了其对称的影响；）
也就是说狭义相对论不过是平面走着走着同时还在转动，在四维空间里是一个洛伦兹旋转群罢了；

所以聪明的你也应该发现了，好像数学模型对应的物理情况总能在物理中找到，或许你在数学中从未有实际对应的理论会有重大意义呢。

我们继续，我们是为了什么才说的光速不变呢，是为了说光对于两次物理革命的贡献，对吧！
第二次关于对光的革命即使量子力学，让我们走近quantum physics,看看他到底在讲些什么！

四，quantum pyhscis：
其实量子力学还是比较完善的一门学科！它的很多理论非常自洽，而且更加数学而非像是相对论那种拼凑起来的理论；用数学工具强行的解决一块一块问题，像是一个煎饼果子；
量子力学对于光的最大贡献其实是光场的再次量子化，就是把所谓量子场论，（标量场）
“光子是唯一一个在作为粒子之前被当成场探测的粒子. 因此发展量子场论形式体系的第一个
实例与辐射相联系是十分自然的, 直到后来, 才应用到其它粒子和场.”
————温伯格
；
一，初步唯象低速理论：
什么是量子力学？
答：量子力学是建立在希尔伯特空间的符合酋变换的可测量复合系统；
（希尔伯特空间我不在解释我第一章有）
酋变化就是指随着时间的演化他的绝对值不变；
可测量就是算子符合投影定则，（某个特征值的测量概率等于这个态在总体中的占有比）
复合系统也就是可以用张量积来直乘他的不同基从而形成系统的基；（比如自旋————空间耦合，描述自选一组基，空间耦合一组基，直乘即可描述复合系统也即是自旋空间耦合态；）

量子力学为了描述粒子的波动性（波动性代表概率，在实验中仍然使用全同粒子系综去确定，而非单个粒子（这样可能与纠缠态？所以可能并不是随机的）），仍然采用经典波动方程去描述事件，

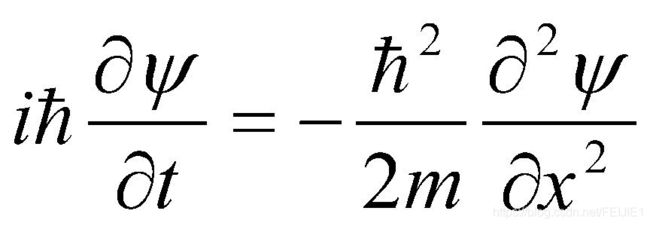
$$当波=exp(iEt-iPx)；d波/dt=iE\ast 波；d波/dx=-ip\ast 波；$$
$$d波/(iE\ast dt)=波；d波/(-ip\ast dx)=波；$$
$$d波/(iE\ast dt)=d波/(-ip\ast dx);$$
而经典理论中：
$$E=P^2/2M;$$
则：
$$d^2波/d^{2}x=-p^2\ast 波；d^2波/d^{2}x=-2M\ast E\ast 波=2M\ast (-i)\ast i\ast E\ast 波；$$
$$d^2波/d^{2}x=2M\ast (-i)\ast d波/dt；$$
这就是薛定谔方程，它的核心思想是：
$$E=P^2/2M;$$
（薛定谔方程，不过是个非相对论波动方程；）
这样我们建立起来一系列理论，然后我们会发现在希尔伯特空间里自然有施瓦茨不等式

这自然会推导出不确定性原理，并且是广义的！
读者可以在格里菲斯的量子力学中找到答案；
好继续，基于希尔伯特空间我们在坐标表象下写出一系列势能（坐标表象下的势能用三维球坐标形式），这样我们需要做两个事：
1，求解在坐标表象下的特征值和向量；
2，如何对应到本力学量的表象下；
这是一个深不可见的数学世界，最后到我们甚至无法精确求解一些简单的散射，只用一些近似，从这个层面上来说，工程师可以超越物理学家！
（实际上，我是个综合学科者，我感受到了光靠科班的局限）
（波恩）
光，作为一个标量场，我们一般是将辐射场也就是矢势量子化；然后写成哈密顿形式，也就是类似于准粒子
如下:

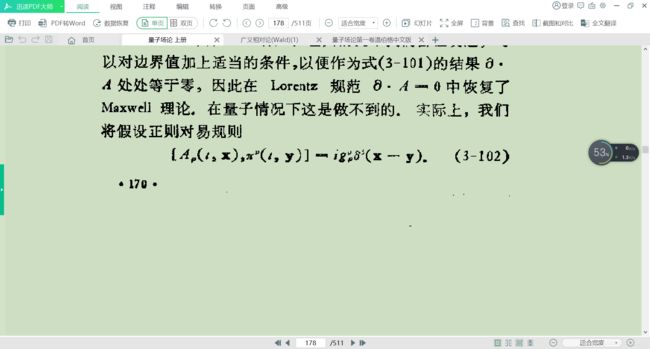
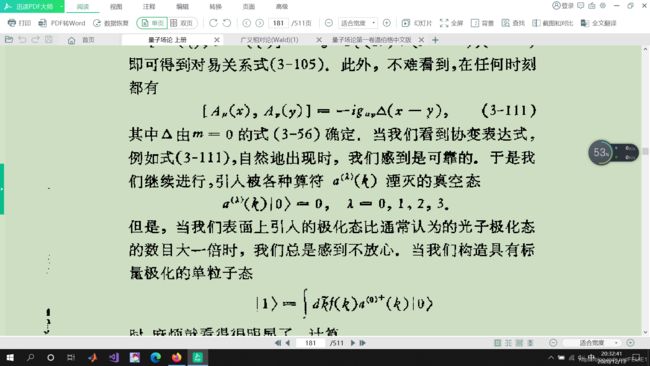别担心，我也看不懂，我们主要看到他把A量子化了，完事；（这是量子场论的内容）

二，相对论性量子理论：
这个时候你不能再用薛定谔方程，因为它的基础是
$$E=P^2/2M;$$
而高速时候：
$$E=M{C}^2;$$
$$E^2=M^2\ast C^4+P^2\ast C^2;$$
所以同样的道理就是用上述方程从exp(iEt-ipx)中解出E，p然后通过上述方程写到一起：


这个方程叫克莱因高等方程;
他就是量子力学过渡到高速的起源，。。。。
然后你懂的，我知道我说得太多了，就此打住！

大家体验了一波精神！嗯，很nice!

五，基本参数（绕了一大圈把什么是光搞清楚了，gg）
很开心，这里绝对没有人了，能看下来的绝对是要么真的很捧场，要么就是瓜皮了。。。
感谢各位咱们来点实在的！
镜头，它是一个有厚度的折射片；
在我的世界里，经典光学的一切效应只能算近似，ok,我们来看看镜头的知识！
back to zero;
1,光电系统的构成：

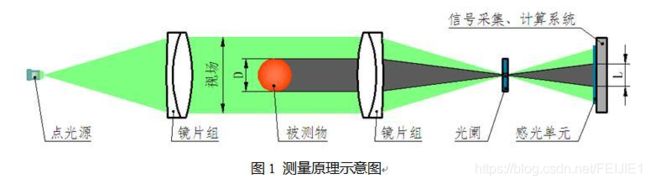
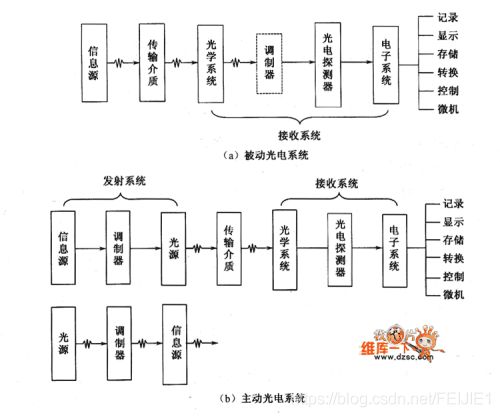
我们已经说了我们是红外仿真，也就是被动的光电系统，
光辐射和大气衰减都说过了，现在传播过来的光将会经过镜片进入到相机，光学系统是将辐射光焦距在探测光焦平面上，然后通过焦平面上的探测器
扫描或者不扫描的方式转换成电信号序列，经过处理后再次在显示器上呈现出来图像；
2,视场：
视场代表着摄像头能够观察到的最大范围，通常以角度来表示，视场越大， 观测范围越大。
瞬时视场角（Instantaneous Field Of View，IFOV），是指传感器内单个探测元件的受光角度或观测视野，它决定了在给定高度上瞬间观测的地表面积，这个面积就是传感器所能分辨的最小单元。IFOV越小，最小可分辨单元越小，图像空间分辨率越高。IFOV取决于传感器光学系统和探测器的大小
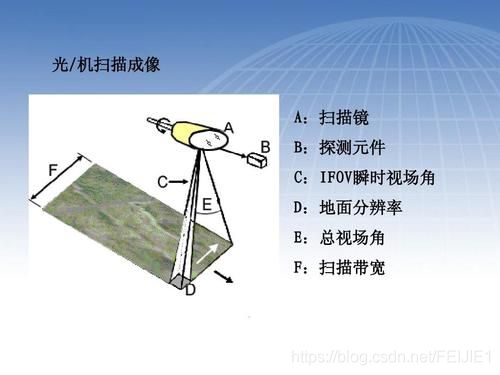3，扫描型成像系统：
顾名思义，扫描型成像系统就是因为探测器的视场角太小了，需要一点一点去扫描了，
很呆，我国所有书上都是一行扫描然后换行，采用这种low的不谈的方法，这里给个网址给那些写书的人看：

希尔伯特曲线：无限数学怎样应用于有限世界（中英字幕）

https://www.bilibili.com/video/av4201747/
这叫希尔伯特曲线扫描法，不会因为扫描设备的漏扫描改变而混乱像素容错率很高，求求你们上点心吧；
4，凝视型成像系统：
凝视型焦平面多用于观测近物，它不是一列探测器，而是直接一个二维的探测面，直接让光电效应记录在每个平面上，当然这样需要的时间响应肯定会差！
5，扫过比：
扫描过程中，相邻的视场可能有重叠或间隙表明这种扫描重叠程度的系数称为扫过比Os。
相邻探测器之间的距离为d,大小为a,那么叫a/d为扫过比；
6,驻留时间
驻留时间就是扫过探测器张角的时间；
总视场像元素：
$$m=Wh\ast Wv/(a\ast b\ast Os);$$;
帧周期：扫过一副完整的画面所需要的时间：Tf ；
扫描效率：由于物理原因回扫时候会产生一个时间差Tf’ ;
单元探测器驻留时间：
$$td=(Tf-T{f}^{\prime })/m；$$
7，时间和频率关系：
$$f(time)=w\ast f(space)=(a/td)\ast f;$$
；
六，重中之重！成像物理过程
1，光学系统的辐射衰减，模糊，几何扭曲和渐晕
2，探测器时空滤波，空间采样，噪声；
3，信号处理的时域滤波，非线性响应和数字滤波；
4，监视器滤波和插值；
系统模型分类：
1，连续输入————连续输出；
2，离散输入————离散输出；
3，连续输入————离散处理————连续输出；
（输入场景分辨率是探测器的16倍，这时我们才能认为输入场景是连续的）
七，本章的重点！：光学系统（衍射，各种像差和扭曲）
本博主罗嗦了一大堆，从光是什么，相对论，量子力学，光学成像，最终终于迎来了：
光学仿真；
没错咱们是光学仿真啊！我都跑题成啥了。。。。
好！来，我们先来对衍射进行分析：
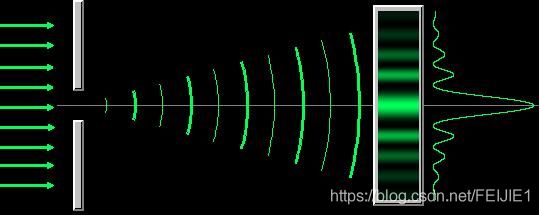1，衍射
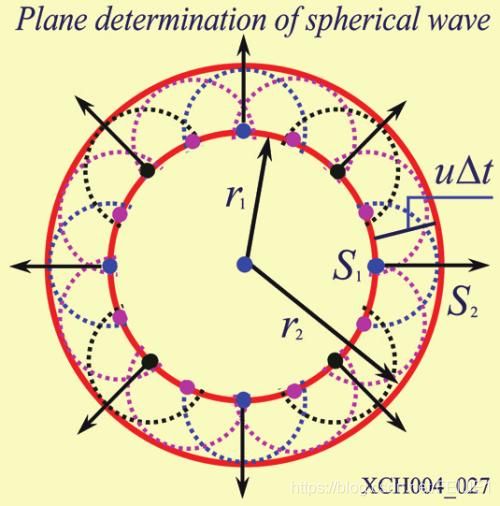
菲涅尔说光是由不断地波前叠加的传播方式；
其实达芬奇的书里早就说了这点，不过达芬奇那时已经去世了。。

（达芬奇）

1818年菲涅尔论证了波动理论的衍射效应，菲涅尔认为波是由波前不断叠加的结果；
之后的基尔霍夫更加数学化了他的理论，并成为了严格意义上的理论；

（菲涅尔）

1896年，索莫非第一次解出了衍射的方程；

（索莫非）
我们假设：
有一定能量的波在传播；那么肯定的沿传播方向的能量最大，做一个角分布：
$$k(th)$$
th是法线和沿某方向传播的夹角，k(th)表示的就是振幅的调节，k(0)最大；
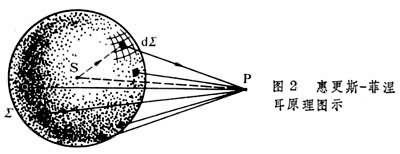
这样在传播面为r0的波面上的某一点（这时作为震源）二次波有：

$$A=A0\ast exp(ikr0)/r0;（是球面上）某点的振幅$$
$$dU(th)=k(th)\ast A\ast exp(iks)/s\ast ds;(发现是球面上这点的法线，角度为指向某一点p的角度)$$

经过基尔霍夫的倾心计算：
$$K（th)=-i/(2\ast lamuda)\ast (1+cos(th));$$
这说明反方向为零，正方向最大，符合我们的直觉；
$$dU(th)=-i/(2\ast lamuda)\ast (1+cos(th))\ast A\ast exp(iks)/s\ast ds$$
$$A=A0\ast exp(ikr0)/r0;（是球面上）某点的振幅$$
这就是衍射的全部内容了，完；
以上公式称为：菲涅尔基尔霍夫积分公式
那么怎么运用它呢？（这里要强调，首先这个是衡稳波面，不随着时间改变，而且介质各向同性， ）
当然就是让它对于波阵面整个去积分，然后得出p点的振幅，
对于可以忽略exp二阶以上的叫————夫琅禾费衍射；
不可以忽略的叫————菲涅尔衍射；

有以下公式：
$$U(p)=\int \int k(th)\ast A0\ast exp(ik(r+s))/rs\ast ds;$$
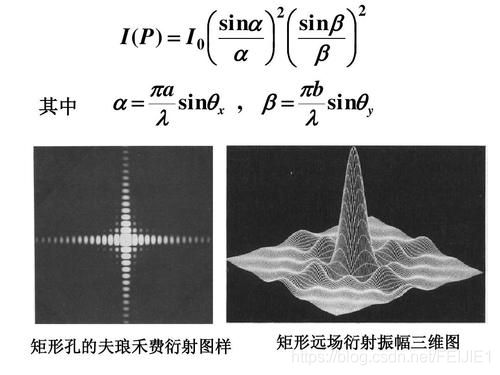
对于方孔（大小a*b）：
$$U(p)=\int \int sqrt(I0)\ast sin(kpa)\ast sin(kpb)/(kpa\ast kpb);$$

其中I0是中心点辐射；
$$I0=sqrt(P\ast d)/(lamuda\ast R);P是入射到孔上的功率d是孔径R是距离lamuda是波长$$
k是波矢
p是余弦之差

这是对于一个不时变的标量系统，如果是一幅图像就是把每一个点到达波阵面的衍射算一下再加起来；也就是卷积 啦，我们认为物体够远，到达时候的波阵面都是平面波，让我们来算一下他的傅里叶卷积核：
$$H=(1-fx/fcx)\ast (1-fy/fcy);$$
fcx,fcy分别是xy方向的截止频率，k是波矢，p是余弦差值，
$$fcx=Dy/lamuda;fcy=Dx/lamuda;$$
我们仍然用matlab去做它的一个演示：

a=imread('C:\Users\ThinkPad\Desktop\光学仿真2\lj.jpg');  %你自己改图片地址就行
figure(1),imshow(a,[]);   %figure(1)里面显示原图
aa=rgb2gray(a);  %转成灰度

aaa=fft2(aa);  
d=input('请输入d');
lamuda=input('请输入lamuda');
fcy=d/lamuda;
fcx=d/lamuda;
aaaa=zeros(size(aaa));
for i=1:size(aaa,1)
    for j=1:size(aaa,2)
   aaaa(i,j)=aaa(i,j)*(1-i/(fcx*size(aaa,1)))*(1-j/(fcy*size(aaa,2)));%这里除以size是因为fft的频率是n/N
    end
end
b=ifft2(aaaa);
figure(2),imshow(b,[]);  

(处理前)

处理后（只有当D比lamuda小时候衍射才明显）（d=1;lamuda=1）

（d=0.1;lamuda=1）

(d=5，lamuda=1)

效果很不错！！！！！
衍射效应也正是如此，我们眯着眼睛看一下灯，会有很多的“线”
这些线就是衍射，跟我们图中的“线”很像，衍射是成功的！
吼吼！！！
落地一个了！

同样的对于圆孔衍射也有：
$$U(p)=2\ast J1(kaw)/(kaw)\ast sqrt(I0);$$
Jn是贝塞尔函数；
它的傅里叶为
$$H(fx,fy)=2/pi\ast [arcos(fx/fc)-fx/fc\ast sqrt(1-(fx/fc{)}^2)];$$
给你们个机会！写个程序仿真一下圆孔衍射！

喝口水，下一篇讲解 像差和畸变等其他光学传递函数；
光学仿真三千问（讲人话）

（第二篇———光学(第一小节)）
完