函数递归-------套娃套路深,要么你玩递归,要么递归玩你
目录
什么是递归?
递归的两个必要条件
递归与迭代
____________________________________________
什么是递归?
程序调用自身的编程技巧称为递归( recursion )。
递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接
调用自身的
一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,
递归策略
只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小
简单的来讲就是 不断的套用自身的函数来达到能多次跟循环一样的效果,且代码简单
递归的两个必要条件
(1)存在限制条件,当满足这个限制条件的时候,递归便不再继续。
(2)每次递归调用之后越来越接近这个限制条件
简单说就是需要判断,调用自身的时候传入的参数不能和原函数相同,
可能有些小可爱们还是不怎么理解,那我们来操作一下:
练习1;
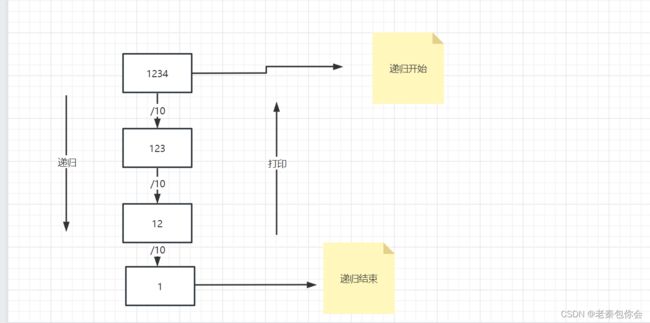
接受一个整型值(无符号),按照顺序打印它的每一位
如输入1234,就打印出1234
思路:
当只有个位数直接打印即可,当超过1位数,我们用%10来得出余数,打印余数
代码如下:
void My_print(unsigned int inp)//正向打印
{
if(inp/10)
{
My_print(inp/10);
}
printf("%d",inp%10);
}
void My_print_(unsigned int inp)//反向打印
{
printf("%d",inp%10);
if(inp/10)
My_print_(inp/10);
}
int main()
{
unsigned int inp=0;
printf("请输入数字:>");
scanf("%d",&inp);
My_print(inp);
return 0;
}运行结果:
递归第一步是要先判断条件,写明判断条件就可以避免死循环
可能一题还不足以学会,我们接着来:
练习2:
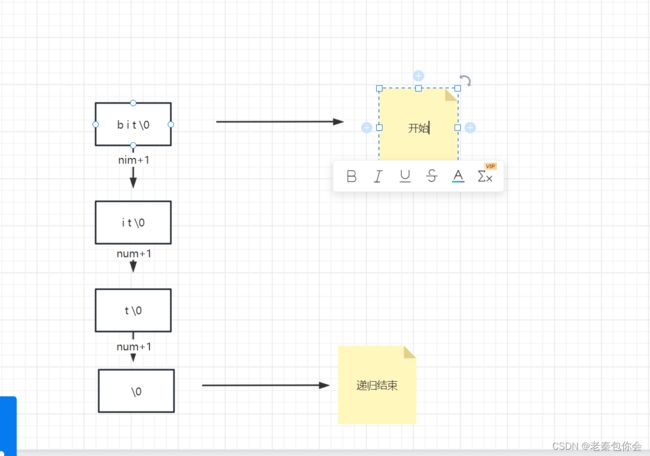
编写函数不允许创建临时变量,求字符串的长度
思路:
在c语言中有strlen()计算字符串个数不计算'\0',我采用的是这个思路,
代码如下:
#include
int num_strlen(char* arr)
{
if(*arr!='\0')
{
return (1+num_strlen(arr+1));
}
return 0;
}
int main()
{
char arr[]="bit";
int num=num_strlen(arr);//传入的是数组的首元素地址
printf("长度为%d",num);
return 0;
}
每次递归时,传入的字符串数都是一个,当传入的字符为'\0'就停止递归下去
这两题可能还是一些小可爱不怎么理解,我们就在来一题
练习3:
求n的阶乘
!n=n*(n-1)*...*1=n*!(n-1)
思路:
代码如下:
#include
int My_num(int n)
{
if (n == 1)
return 1;
else
{
return n * My_num(n - 1);
}
}
int main()
{
int n = 0;
printf("输入你想计算的阶乘:(数字)");
scanf("%d", &n);
int num = My_num(n);//返回计算结果
printf("%d的阶乘结果为:%d", n, num);
return 0;
} 结果:
看到这里有些小可爱们有眉目了
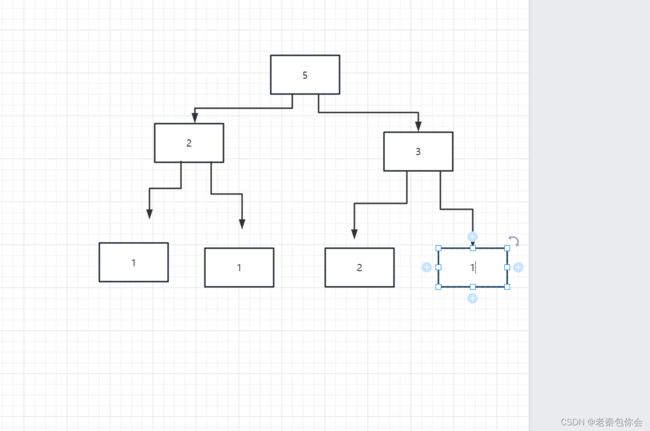
那我们就开始练习一下斐波那契数。
斐波那契数:
1,1,2,3,5.........
从第三个数开始该数等于两数之和,2==1+1,3=2+1,5=3+2
思路:
我们主要捉住重点就是前两数之和等于第三个数 当我们要求出第几位的斐波那契数,我们只需求出前两数即可
代码如下:
#include
int My_num(int n)
{
if (n <= 2)
return 1;
else
return My_num(n - 1) + My_num(n - 2);//记住My_num()输入位置返回该位置的斐波那契数,因为该位置的斐波那契数等于前两数之和,只需前两数之和就行
}
int main()
{
int n = 0;
printf("你要求出第几位的斐波那契数:>");
scanf("%d", &n);
int num = My_num(n);//传入n返回斐波那契数数
printf("第%d位的斐波那契数为%d", n, num);
return 0;
}
结果:
当我们输入越来越大的值就会发现,运行时间越来越长,因为递归也是有缺陷的,会重复大量的工作,这是使用递归不可避免的
#include
int My_num(int n)
{
int a = 1;
int b = 1;
while (n>2)
{
int d = a + b;
a = b;
b = d;
n--;
}
return b;
}
int main()
{
int n = 0;
printf("你要求出第几位的斐波那契数:>");
scanf("%d", &n);
int num = My_num(n);//传入n返回斐波那契数数
printf("第%d位的斐波那契数为%d", n, num);
return 0;
} 这是非递归的,运行速度就很快
所以建议:
1. 许多问题是以递归的形式进行解释的,这只是因为它比非递归的形式更为清晰。
2. 但是这些问题的迭代实现往往比递归实现效率更高,虽然代码的可读性稍微差些。
3. 当一个问题相当复杂,难以用迭代实现时,此时递归实现的简洁性便可以补偿它所带来的运行时开 销
总结
递归总的来说是一种方法,在解决问题中我们要用最简单有效的方法进行解决问题,递归很好用,但使用要看场景