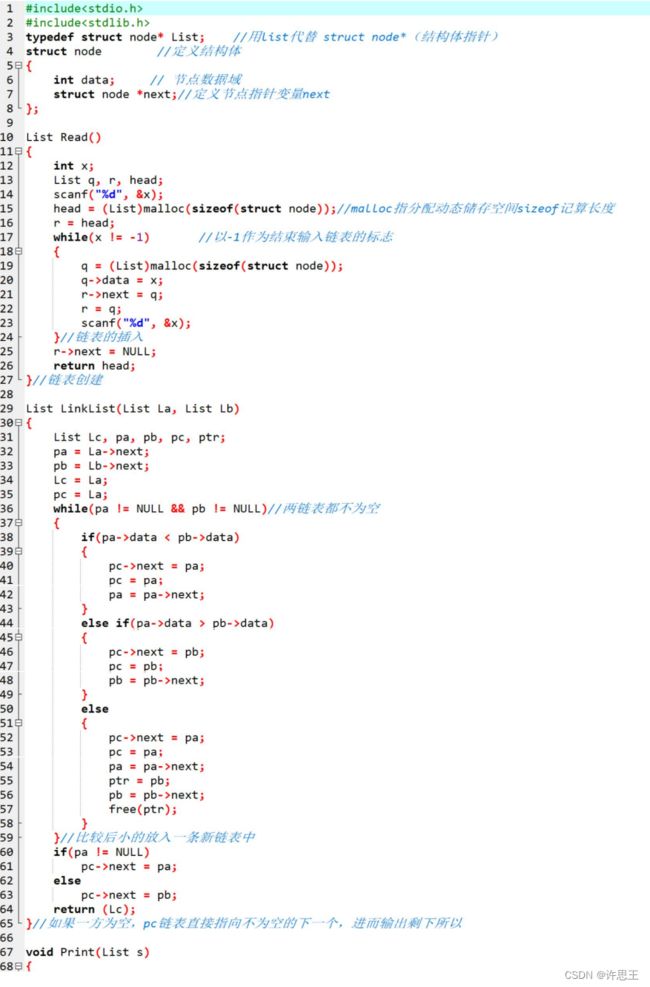
数据结构与算法---单向链表
千教万教教人求真,千学万学学做真人—陶行知
文章目录
- 单向链表的定义
- 单向链表的实现
-
- 初始化
- 单向链表的创造
- 头插法
- 尾插法
- 插入
- 删除
- 整个单向链表
- 每日一题
- 答案及解析
(a1,a2,a3…an)
的链式存储结构。又由于此链表的每个结点中只包含一个指针域, 故又称线性链表或单链表。根据链表结点所含指针个数、指针指向和指针连接方式,可将链表分为单链表、循环链表、双向链表、二叉链表、十字链表、邻接表、邻接多重表等。其中单链表、循环链表和双向链表多用于实现线性表的链式存储结构,其他形式多用于实现树和图等非线性结构。
单向链表的定义
线性表的单链表存储结构,整个链表的存取必须从头指针开始进行,头指针指示链表中第一个结点 (第一个数据元素的存储映像,也称首元结点)的存储位置。同时,由于最后一个数据元素没有 直接后继,则单链表中最后一个结点的指针为空(NULL)。

用单链表表示线性表时,数据元素之间的逻辑关系是由结点中的指针指示的,指针为数据元素之间的逻辑关系的映像,则逻辑上相邻的两个数据元素其存储的物理位置不要求紧邻,由此,这种存储结构为非顺序映像或链式映像。
通常将链表画成用箭头相链接的结点的序列,结点之间的箭头表示链域中的指针。为在使用链表时,关心的只是它所表示的线性表中数据元素之间的逻辑顺序,而不是每个数据元素在存储器中的实际位置。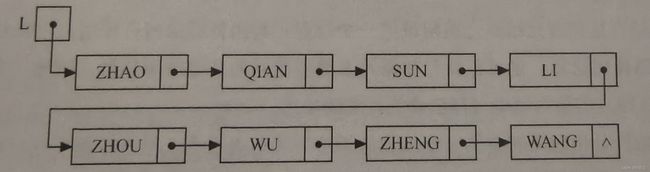
单向链表的实现
初始化
单向链表的初始化操作就是构造一个存放数据的空表。
在表中我们需要定义我们所需的数据元素,及存放下一个结点地址元素
typedef int Elemtype;
typedef struct Node
{
Elemtype length;
struct Node* next;
}Node;
注:此处Elemtype 被定义为整型,因此我们可以使用头结点的数据元素保存链表长度。
单向链表的创造
在使用单向链表之前我们得先创建表头,这个表结点中不存放任何元素(又整型元素时也可用来存放链表长度),在头结点中我们通产将存放的下一个结点的指针赋值为零。并返回该结点的指针
Node* Creat_list()
{
Node *head= (Node*)malloc(sizeof(*head));
if (head == NULL)
return NULL;
head->length = 0;
head->next = NULL;//初始化
return head;
}//创建头链表
头插法
头插法是通过将新结点逐个插入链表的头部(头结点之后)来创建链表,每次申请一个新结点,读人相应的数据元素值,然后将新结点插人到头结点之后。
生成一个新结点*p;
输人元素值赋给新结点*p的数据域;
将新结点*p插人到头结点之后。
前插法的创建过程,因为每次插人在链表的头部,所以应该逆位序输人数据,依次输人e、d、C、b、a,输入顺序和线性表中的逻辑顺序是相反的。
void Input_List_Head(Node*head,Elemtype data)
{
Node* newNode = (Node*)malloc(sizeof(Node));//创建新的结点
newNode->length = data;//赋值
newNode->next = head->next;//
head->length++;//头结点记录链表长度,长度增加
head->next = newNode;//与头结点相连接
}//头插法
尾插法
尾插法是通过将新结点逐个插人链表的尾部来创建链表。同头插法一样, 每次申请个新结点,读入相应的数据元素值。不同的是,为了使新结点能够插人表尾。需要增加一个尾指针r指向链表的尾结点。
生成一个新结点*p;
●输人元素 值赋给新结点*p的数据域;
●将 新结点p插人尾结点r之后;
●尾指针r指向新的尾结点*p。
尾插法的创建过程,读入数据的顺序和线性表中的逻辑顺序是相同的。
void Input_List_Afterbody(Node* head, Elemtype data)
{
Node* newNode = (Node*)malloc(sizeof(Node));//创建新的结点
newNode->length = data;//为结点赋值
newNode->next = NULL;//初始化结点
Node* list = head->next;
while (list->next)
{
list = list->next;
}//遍历结点找到链表的末尾
list->next = newNode;
head->length++;//链表长度加一
}//尾插法
插入
将值为e的新结点插人表的第1个结点的位置,即插人结点ai-1与ai之间,
查找结点ar并由指针p指向该结点。
生成一个新结点s。
1.将新结点s的数据域置为e。
2.将新结点s的指针域指向结点ai
3.将结点p的指针域指向新结点*s。
int Input_List_Insert(Node*head,Elemtype data,int i)
{
int j = 0;
if (i > head->length||i<0)
{
printf("Error");
return Error;
}//判读该链表长度是否超出i
Node* newNode = (Node*)malloc(sizeof(Node));//构造新的结点
newNode->length = data;//赋值
Node* list = head->next;
while (i!=j)
{
list = list->next;
j++;
}//寻找第i个链表
Node* list_last = list;//保存修改前的第i的链表的地址
list->next = newNode;//插入链表元素
newNode->next = list_last;//将修改后的链表与之前断裂处相连接
return 0;//还有返回值
}//插入数据
和顺序表一样,如果表中有n个结点,则插入操作中合法的插入位置有n+1个,即1≤i≤n+1。当i=n+I 时,新结点则插在链表尾部
注:单链表的插入操作虽然不需要像顺序表的插入操作那样移动元系,但其平均时间复杂度仍为O(n)。这是因为,为了在第i个结点之前插入一个新结点,必须首先找到第i-1个结点,其时间复杂度与查找算法相同。
删除
要删除单链表中指定位置的元素,同插入元素一样, 首先应该找到该位置的前驱结点,但在删除该结点时,除了修改前驱结点的指针域外,还要释放结点本身所占的空间,所以在修改指针前,应该引人另一指针q,临时保存本身结点的地址以备释放。
1.查找结点a;并由指针p指向该结点。
2.临时保存待删除结点a的地址在q中,以备释放。
3.将结点*p的指针域指向a,的直接后继结点。
4.释放结点a的空间。
int Delelt_List_Locate(Node* head, int i)
{
int j = 0;
if (i > head->length || i < 0)
{
printf("Error");
return Error;
}//判读该链表长度是否超出i
Node* list = head->next;
Node* previousNode = head;
while (i != j)
{
previousNode = list;
list = list->next;
j++;
}//寻找第i个链表
previousNode->next = list->next;//保留该结点保存的下一个结点地址
free(list);//释放当前结点
head->length--;//长度减一
}//删除第i个结点
int Delelt_list_Data(Node*head,Elemtype data)
{
Node* list = head->next;
Node* previousNode = head;
while (list)
{
if (list->length == data)
{
previousNode->next = list->next;
free(list);
head->length--;
return 1;
}
list = list->next;
previousNode = list;
}
return 0;
}//按数据查找删除
int Clear_List(Node* head)
{
Node* p, *q;
p = head->next;
while (p)
{
q = p->next;
free(p);
p = q;
}
head->next = NULL;
}//释放链表
注:删除算法中的循环条件(p->next&&j 输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。整个单向链表
#include每日一题
示例1:
输入:1->2->4->10, 1->3->4
输出:1->1->2->3->4->4->10
最后的话 :如果大家觉得这篇文章对你们有帮助的话希望你们能够点点关注,你们的关注是我继续写下去的动力,谢谢大家。

(文章中图片与部分内容来源与网络,如有侵权请联系删除)答案及解析